Five Less Than A Number Is Greater Than Twenty
faraar
Sep 15, 2025 · 7 min read
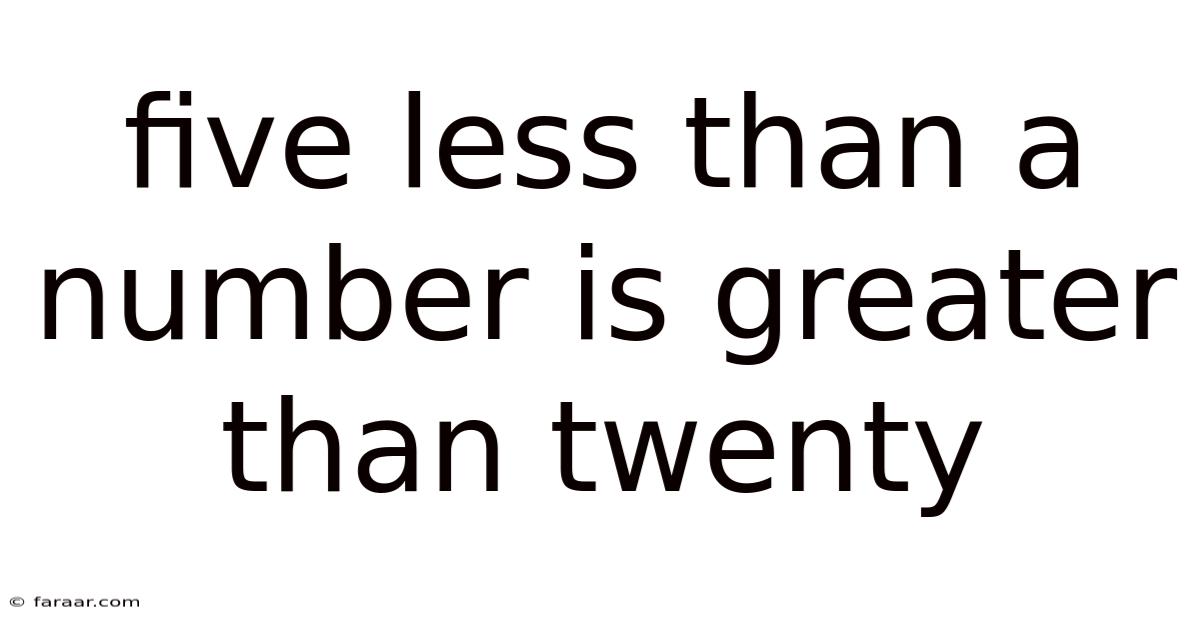
Table of Contents
Five Less Than a Number Is Greater Than Twenty: Understanding and Solving Inequalities
This article explores the mathematical inequality "five less than a number is greater than twenty." We'll break down how to translate this phrase into a mathematical expression, solve for the unknown number, graph the solution, and delve into the broader concept of inequalities. This seemingly simple problem opens a door to understanding a crucial area of algebra and its applications in real-world scenarios. We'll cover everything from the basic steps to more advanced considerations, making it accessible to learners of all levels.
Understanding the Problem: From Words to Math
The phrase "five less than a number" immediately suggests subtraction. We're taking five away from an unknown quantity. Let's represent this unknown number with the variable x. Therefore, "five less than a number" translates to x - 5.
The phrase "is greater than twenty" signifies an inequality. It's not an equation where both sides are equal; instead, one side is explicitly larger than the other. The symbol for "greater than" is >.
Combining these elements, we arrive at the complete mathematical inequality:
x - 5 > 20
This simple expression encapsulates the entire problem statement. Now, let's move on to solving it.
Solving the Inequality: Finding the Values of x
Solving inequalities is similar to solving equations, but with one key difference: when you multiply or divide by a negative number, you must reverse the inequality sign. Let's solve our inequality step-by-step:
-
Isolate the variable: Our goal is to get x by itself on one side of the inequality. To do this, we add 5 to both sides:
x - 5 + 5 > 20 + 5
This simplifies to:
x > 25
This means that any number greater than 25 satisfies the original inequality "five less than a number is greater than twenty."
Graphical Representation: Visualizing the Solution
Inequalities can be visually represented on a number line. This provides a clear and concise way to understand the range of solutions.
To graph the solution x > 25, we would:
- Draw a number line: Create a horizontal line with numbers marked on it, including 25.
- Mark 25: Place a point at 25 on the number line.
- Indicate the direction: Since x is greater than 25, we draw an open circle (or parenthesis) at 25 to show that 25 itself is not included in the solution. Then, we draw an arrow pointing to the right, indicating all numbers greater than 25 are part of the solution.
The graph visually represents all possible values of x that satisfy the inequality.
Exploring the Concept of Inequalities: Beyond the Basics
The simple inequality we've solved, x - 5 > 20, introduces us to a much broader mathematical concept: inequalities. Inequalities are mathematical statements comparing two expressions using inequality symbols such as:
- > (greater than)
- < (less than)
- ≥ (greater than or equal to)
- ≤ (less than or equal to)
- ≠ (not equal to)
These symbols allow us to express a range of relationships between numbers and expressions, making them indispensable tools in various fields.
Real-World Applications of Inequalities
Inequalities are not just abstract mathematical concepts; they have numerous practical applications in everyday life and various fields:
-
Budgeting: Determining how much money you can spend without exceeding your budget involves inequalities. For example, if you have $100 and want to buy items costing x dollars, you'd need to ensure x ≤ 100.
-
Scheduling: Planning your day involves considering time constraints. If you have a 2-hour window to complete tasks taking x hours each, you need to ensure x ≤ 2.
-
Engineering: Designers and engineers use inequalities to ensure structures can withstand certain loads and stresses. A bridge, for example, must be designed to handle a weight x that is greater than or equal to a specified maximum load.
-
Economics: Supply and demand curves are described using inequalities. For instance, the price of a product will often increase if the demand (represented by x) is greater than the supply.
-
Computer Science: Inequalities are fundamental to algorithms and data structures. Sorting algorithms, for example, often rely on comparisons using inequality symbols to arrange data in order.
These examples demonstrate the practical importance of understanding and working with inequalities.
Solving More Complex Inequalities: Multiple Steps and Compound Inequalities
While x - 5 > 20 is a relatively straightforward inequality, many real-world problems involve more complex expressions. These might require multiple steps to isolate the variable or involve compound inequalities.
A compound inequality combines two or more inequalities using words like "and" or "or." For example:
-
x > 10 and x < 20 This means x must be greater than 10 and less than 20. The solution would be 10 < x < 20, representing a range of values between 10 and 20 (excluding 10 and 20 themselves).
-
x < 5 or x > 15 This means x can be less than 5 or greater than 15. The solution is two separate ranges.
Let's consider a more complex example:
3x + 7 ≤ 16
-
Subtract 7 from both sides: 3x ≤ 9
-
Divide both sides by 3: x ≤ 3
This inequality is solved in a similar manner to our initial example, demonstrating the consistent application of algebraic principles. Remember to always pay close attention to the inequality sign, reversing it if you multiply or divide by a negative number.
Absolute Value Inequalities: Adding Another Layer of Complexity
Absolute value inequalities introduce another layer of complexity. The absolute value of a number is its distance from zero, always non-negative. The absolute value symbol is denoted by | |.
For example, |x| = 5 means x could be either 5 or -5, since both are 5 units away from 0.
Let's consider the inequality:
|x - 2| > 3
This inequality means the distance between x and 2 is greater than 3. This translates into two separate inequalities:
- x - 2 > 3 or x - 2 < -3
Solving each separately:
- x > 5 or x < -1
Therefore, the solution is x > 5 or x < -1, representing two distinct ranges of values.
Frequently Asked Questions (FAQ)
Q: What happens if I multiply or divide an inequality by a negative number?
A: When you multiply or divide both sides of an inequality by a negative number, you must reverse the direction of the inequality symbol. For example, if you have -2x < 6, dividing by -2 gives x > -3 (notice the < changed to >).
Q: How can I check if my solution to an inequality is correct?
A: Substitute a value from your solution set into the original inequality to see if it makes the statement true. If it does, your solution is likely correct. You can also test values outside your solution set to confirm they make the inequality false.
Q: What is the difference between an equation and an inequality?
A: An equation uses an equals sign (=) to show that two expressions are equal. An inequality uses an inequality symbol (>, <, ≥, ≤, ≠) to show that two expressions are not necessarily equal but have a specific relationship in terms of their size or value.
Q: Can inequalities have infinite solutions?
A: Yes, many inequalities have an infinite number of solutions. For example, x > 5 has infinitely many numbers that are greater than 5.
Conclusion: Mastering Inequalities – A Foundation for Further Learning
Understanding and solving inequalities is a fundamental skill in mathematics and has widespread applications in various fields. Starting with a simple statement like "five less than a number is greater than twenty," we've explored the process of translating words into mathematical expressions, solving the inequality, graphing the solution, and delving into more complex scenarios involving compound inequalities and absolute values. This foundational knowledge serves as a stepping stone towards more advanced mathematical concepts and problem-solving skills, equipping you with tools to tackle real-world challenges effectively. Remember to practice regularly and seek clarification whenever necessary – mastering inequalities opens doors to a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
Parent Function Of A Quadratic Equation
Sep 15, 2025
-
Can You Say And Or In An Essay
Sep 15, 2025
-
How To Get Denominator By Itself
Sep 15, 2025
-
Perform The Indicated Operation And Simplify
Sep 15, 2025
-
1 Rabbit Saw Six Elephants Answer
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Five Less Than A Number Is Greater Than Twenty . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.