Find Two Fractions That Are Between 3/5 And 4/5
faraar
Sep 13, 2025 · 5 min read
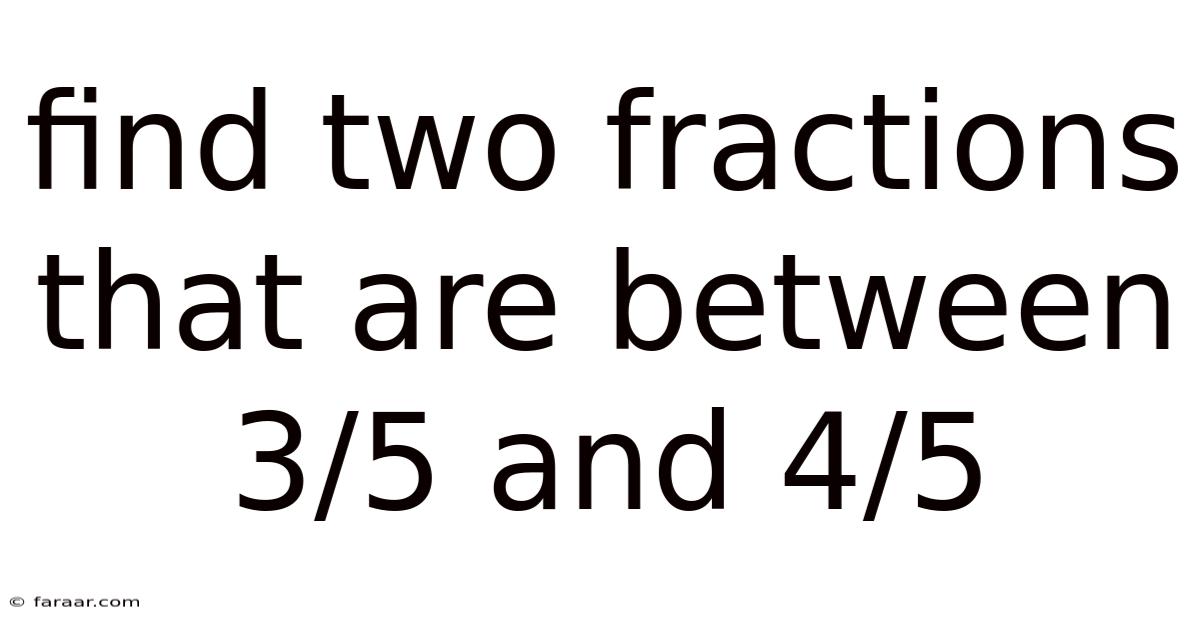
Table of Contents
Finding Fractions Between 3/5 and 4/5: A Deep Dive into Rational Numbers
Finding fractions between two given fractions might seem like a simple task, but it opens up a fascinating world of mathematical concepts and techniques. This article will guide you through several methods to find two fractions between 3/5 and 4/5, exploring the underlying principles of rational numbers and offering a deeper understanding of fraction manipulation. We'll move beyond simply finding a solution and delve into how to find many solutions, and how to understand the infinite possibilities within this seemingly limited space.
Understanding Rational Numbers and Fractions
Before we begin our quest to find fractions between 3/5 and 4/5, let's establish a solid foundation. A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. Fractions are simply a way to represent these rational numbers.
The fractions 3/5 and 4/5 are both rational numbers. They represent points on the number line, with 3/5 lying before 4/5. The task is to find two other rational numbers that reside between these two points.
Method 1: Finding a Common Denominator
This is the most straightforward approach. The key here is to find a common denominator larger than 5. By increasing the denominator, we effectively create more "space" between the fractions, allowing us to insert other fractions.
Let's choose a common denominator of 10. We convert 3/5 and 4/5 to have this denominator:
- 3/5 = (3 x 2) / (5 x 2) = 6/10
- 4/5 = (4 x 2) / (5 x 2) = 8/10
Now, it becomes apparent that 7/10 lies neatly between 6/10 and 8/10. Similarly, we can choose another common denominator, for instance, 100:
- 3/5 = 60/100
- 4/5 = 80/100
We now have a larger range to work with. Several fractions fit comfortably between 60/100 and 80/100. For example:
- 65/100
- 70/100 (or 7/10)
This method highlights the principle that increasing the denominator creates more space for additional fractions.
Method 2: Averaging the Fractions
This method elegantly leverages the concept of averages. We can find a fraction between 3/5 and 4/5 by simply averaging the two fractions. The average of two numbers is found by adding them and dividing by 2.
Let's find the average of 3/5 and 4/5:
(3/5 + 4/5) / 2 = (7/5) / 2 = 7/10
This confirms our finding from Method 1: 7/10 lies exactly halfway between 3/5 and 4/5. However, we need two fractions. To find a second fraction, we can average one of the original fractions with the newly found average:
Average of 3/5 and 7/10:
(3/5 + 7/10) / 2 = (6/10 + 7/10) / 2 = 13/20
Therefore, we have found two fractions: 7/10 and 13/20, both of which are between 3/5 and 4/5. This method neatly demonstrates how averaging provides a methodical way to generate fractions within a given range.
Method 3: Using Decimal Representations
Converting fractions to decimals offers another approach. Let's convert 3/5 and 4/5 to decimals:
- 3/5 = 0.6
- 4/5 = 0.8
Now, finding decimals between 0.6 and 0.8 is straightforward. For example:
- 0.65 = 65/100 = 13/20
- 0.7 = 7/10
This confirms our previous results and shows how decimal representation can facilitate finding fractions between two given values. This method particularly helps visualize the space between fractions on a number line.
Method 4: Infinite Possibilities – A Deeper Dive
The previous methods provide specific solutions, but it's crucial to understand that there are infinitely many fractions between any two distinct rational numbers. This is a fundamental property of rational numbers and their density on the number line.
Consider this: After finding 7/10 as the average, we could apply Method 2 repeatedly. We could average 3/5 and 7/10, then average the result with 7/10, and so on, generating an infinite sequence of fractions between 3/5 and 4/5.
Similarly, we can use any common denominator larger than 5 and find many fractions fitting between the equivalent representations. The larger the denominator, the more fractions we can find. This underscores the infinite density of rational numbers.
Understanding the Density of Rational Numbers
The ability to find infinitely many fractions between any two distinct rational numbers highlights the concept of density. It means that no matter how close two rational numbers are, there will always be another rational number between them. This is unlike integers, where there are gaps between consecutive numbers.
This density of rational numbers has significant implications in various mathematical fields, including calculus and analysis, where it forms the basis for concepts like limits and continuity.
Frequently Asked Questions (FAQ)
Q: Is there a single "correct" answer to this problem?
A: No. There are infinitely many fractions between 3/5 and 4/5. The methods presented show different ways to find some of these fractions.
Q: Can I use negative fractions?
A: While this problem deals with positive fractions, the principle of finding fractions between two rational numbers applies equally to negative ones.
Q: How can I find fractions that are closer to 3/5?
A: By choosing larger denominators and carefully selecting numerators, you can create fractions arbitrarily close to 3/5 (or 4/5) while still remaining between them.
Conclusion: Beyond Simple Fraction Manipulation
This article has explored several effective methods to find two fractions between 3/5 and 4/5. We went beyond merely finding a solution to uncover the deeper mathematical concepts underlying fraction manipulation. The infinite number of possibilities emphasizes the density of rational numbers on the number line, a concept crucial to higher-level mathematics.
This exploration provides a solid foundation for understanding more advanced mathematical concepts and strengthens your skills in working with fractions. Remember that mathematics is not just about finding answers but about understanding the underlying principles and their wide-ranging implications. The journey of finding fractions between 3/5 and 4/5 has led us to a deeper appreciation of the beauty and elegance of rational numbers.
Latest Posts
Latest Posts
-
Using Like Or As Simile Or Metaphor
Sep 13, 2025
-
Find The Measure Of Angle K
Sep 13, 2025
-
How Many Cups Are In 5 Gallons Of Water
Sep 13, 2025
-
How To Find B In A Quadratic Equation
Sep 13, 2025
-
How To Know If A Line Is Parallel
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Find Two Fractions That Are Between 3/5 And 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.