Find Two Fractions Between 3 5 And 4 5
faraar
Sep 21, 2025 · 6 min read
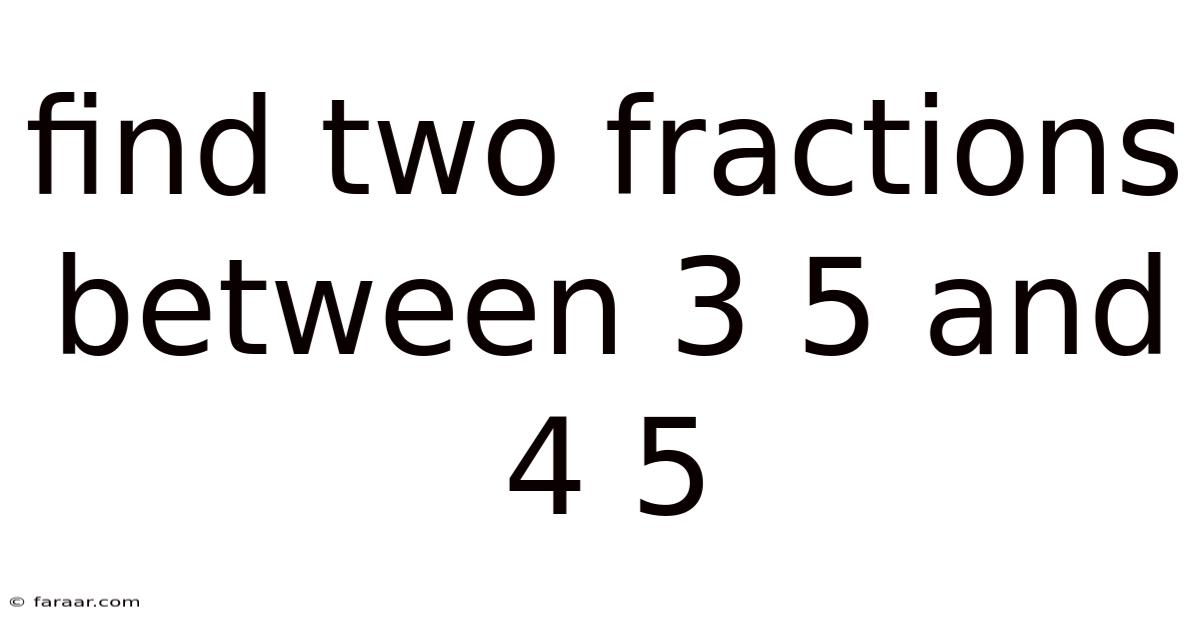
Table of Contents
Finding Fractions Between 3/5 and 4/5: A Deep Dive into Rational Numbers
Finding fractions between two given fractions might seem like a simple task, but it unveils a fascinating world of rational numbers and mathematical principles. This article will explore multiple methods to find not just two, but many fractions between 3/5 and 4/5, providing a comprehensive understanding of the underlying concepts and practical techniques. We will also address common misconceptions and delve into the infinite nature of rational numbers between any two distinct fractions.
Introduction: Understanding Rational Numbers
Before we dive into finding fractions between 3/5 and 4/5, let's establish a foundational understanding. Rational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero. Fractions are a common representation of rational numbers. The numbers 3/5 and 4/5 are both rational numbers, represented as fractions. The key to finding fractions between them lies in manipulating their representations to create new rational numbers within that range.
Method 1: Finding the Average
The simplest method to find a fraction between 3/5 and 4/5 is to calculate their average. This gives us a midpoint between the two fractions.
- Add the two fractions: 3/5 + 4/5 = 7/5
- Divide the sum by 2: (7/5) / 2 = 7/10
Therefore, 7/10 is a fraction precisely halfway between 3/5 and 4/5. This method provides one fraction, but we need two. To find a second fraction, we can repeat this process using either 3/5 and 7/10 or 7/10 and 4/5.
Let's use 3/5 and 7/10:
- Add the two fractions: 3/5 + 7/10 = (6/10) + (7/10) = 13/10
- Divide the sum by 2: (13/10) / 2 = 13/20
So, 13/20 is another fraction between 3/5 and 4/5. We've successfully found two fractions: 7/10 and 13/20.
Method 2: Increasing the Denominator
This method exploits the fact that there are infinitely many equivalent fractions for any given fraction. By increasing the denominator, we create opportunities to find fractions within the desired range.
Let's start with 3/5. To find equivalent fractions, we multiply both the numerator and the denominator by the same integer. Let's multiply by 2:
3/5 * 2/2 = 6/10
Now let's multiply by 3:
3/5 * 3/3 = 9/15
We can see that 6/10 is between 3/5 and 4/5 (or 8/10). Similarly, let's do the same for 4/5:
4/5 * 2/2 = 8/10 4/5 * 3/3 = 12/15
Now we have several fractions: 6/10, 7/10, 8/10, 9/15, and 12/15. We can select any two that lie between 3/5 and 4/5. For example, 6/10 and 7/10 are two such fractions.
This method demonstrates that there are many fractions between 3/5 and 4/5; we are only limited by the extent to which we increase the denominator.
Method 3: Converting to Decimal Representation
Converting fractions to decimal representation can offer a clearer visual understanding of their relative positions.
3/5 = 0.6 4/5 = 0.8
Now, finding decimals between 0.6 and 0.8 is relatively straightforward. For example:
0.65 = 65/100 = 13/20 0.7 = 7/10
Therefore, 13/20 and 7/10 are two fractions between 3/5 and 4/5. This method offers a practical approach, particularly when dealing with more complex fractions.
Method 4: Finding a Common Denominator and Inserting Numerators
This method directly addresses the core concept of finding fractions between two given fractions. We aim to find a common denominator for both fractions that is larger than their original denominators.
The fractions are 3/5 and 4/5. Let's choose a common denominator of 10:
3/5 = 6/10 4/5 = 8/10
Now it's clear that 7/10 lies between 6/10 and 8/10. We could also use a denominator of 15, 20, 25, or any larger number. The higher the denominator, the more potential fractions there are to choose from.
For instance, using a denominator of 20:
3/5 = 12/20 4/5 = 16/20
Now, several fractions are clearly between 12/20 and 16/20, including 13/20 and 14/20 (or 7/10). Thus, 13/20 and 7/10 are our fractions.
The Infinity of Rational Numbers
The methods above illustrate a crucial point: there are infinitely many rational numbers between any two distinct rational numbers. No matter how many fractions we find, we can always find more by increasing the denominator or using more sophisticated techniques. This is a fundamental property of rational numbers and their density on the number line.
Addressing Common Misconceptions
A common misconception is that there are only a few fractions between two given fractions. This is incorrect. The methods discussed above prove that this is untrue.
Another misconception involves assuming that the average method always provides the only fraction between two given fractions. This is incorrect, as demonstrated by the multiple fractions we found. The average simply provides one, and there are many more that exist.
Further Exploration: More Advanced Techniques
For those seeking further exploration, more advanced techniques exist for finding fractions between two given fractions. These include using continued fractions and applying algorithms that systematically generate rational numbers within a specific range.
These techniques go beyond the scope of this basic explanation, but they provide avenues for more in-depth mathematical study for those interested in delving deeper into number theory and rational number analysis.
Frequently Asked Questions (FAQ)
-
Q: Can I use any common denominator? A: Yes, any common denominator larger than the original denominators will work. The larger the denominator, the more fractions you can find.
-
Q: Are there irrational numbers between 3/5 and 4/5? A: Yes, although this article focuses on rational numbers, there are infinitely many irrational numbers between any two real numbers. Irrational numbers cannot be expressed as a ratio of two integers.
-
Q: Why is it important to understand this concept? A: Understanding how to find fractions between two given fractions is fundamental to many areas of mathematics, including calculus, number theory, and computer science, where dealing with rational approximations is crucial.
Conclusion: A Broader Perspective
Finding fractions between 3/5 and 4/5 is more than just a simple mathematical exercise. It's a gateway to understanding the richness and complexity of the rational number system. The infinite nature of rational numbers between any two distinct fractions underscores the vastness of mathematical possibilities. The methods explored – finding the average, increasing the denominator, decimal conversion, and finding common denominators – provide diverse approaches to this seemingly simple problem, revealing the beauty and elegance of mathematical principles. By mastering these techniques, you gain not just the ability to find fractions but also a deeper appreciation for the infinite possibilities within the realm of numbers.
Latest Posts
Latest Posts
-
Who Is My Cousins Cousin To Me
Sep 21, 2025
-
How To Find Domain And Range Of A Linear Function
Sep 21, 2025
-
What Colour Is The Cell Wall
Sep 21, 2025
-
How To Find Length Of A Parallelogram
Sep 21, 2025
-
How To Find Diameter Given Circumference
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Find Two Fractions Between 3 5 And 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.