Find Two Consecutive Numbers Whose Sum Is 115
faraar
Sep 15, 2025 · 5 min read
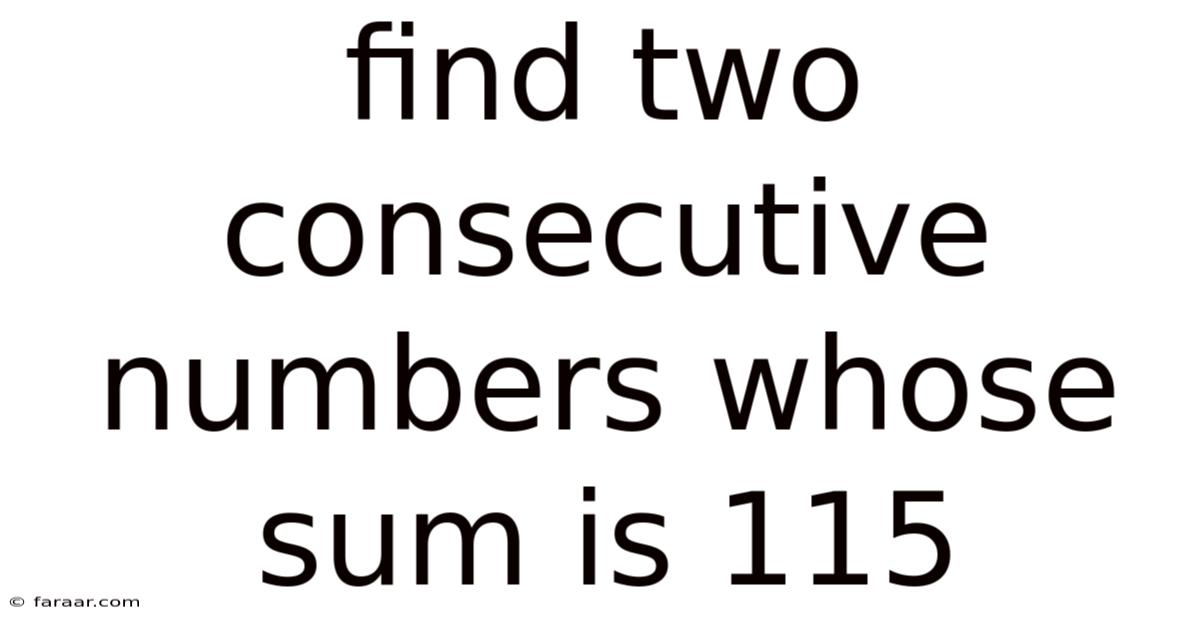
Table of Contents
Finding Two Consecutive Numbers Whose Sum is 115: A Deep Dive into Problem Solving
Finding two consecutive numbers that add up to 115 might seem like a simple problem, but it's a fantastic springboard for exploring various mathematical concepts and problem-solving strategies. This article will guide you through several methods to solve this problem, from intuitive approaches to more formal algebraic techniques. We'll also explore the underlying mathematical principles and delve into how this type of problem can be generalized to more complex scenarios. This is more than just finding the answer; it's about understanding the why behind the solution.
Introduction: Understanding the Problem
The core of the problem is this: we need to find two numbers, x and y, where x and y are consecutive integers (meaning one immediately follows the other), and their sum (x + y) equals 115. This seemingly simple problem allows us to explore fundamental algebraic concepts and develop critical thinking skills. We'll tackle this problem using several approaches, each offering unique insights into the mathematical process.
Method 1: The Intuitive Approach
The most straightforward approach is to use intuition and trial-and-error. Since we're looking for two consecutive numbers, we can start by dividing 115 by 2: 115 / 2 = 57.5. This tells us that the two numbers are likely to be around 57 and 58. Let's check: 57 + 58 = 115. Bingo! We found our solution. This method, while simple for this specific problem, doesn't provide a generalized solution for similar problems with different sums.
Method 2: The Algebraic Approach
This method uses algebra to develop a more robust and generalizable solution. Let's represent the first consecutive number as x. Since the numbers are consecutive, the second number will be x + 1. The problem states that their sum is 115, so we can write the equation:
x + (x + 1) = 115
Now we solve for x:
- Combine like terms: 2x + 1 = 115
- Subtract 1 from both sides: 2x = 114
- Divide both sides by 2: x = 57
Therefore, the first number (x) is 57, and the second number (x + 1) is 58. This algebraic method provides a structured approach that can be adapted to solve similar problems with different sums, making it a powerful tool in your mathematical arsenal.
Method 3: The Arithmetic Sequence Approach
Consecutive integers form an arithmetic sequence with a common difference of 1. We can utilize the formula for the sum of an arithmetic sequence to solve this problem. The formula is:
S<sub>n</sub> = n/2 * [2a + (n - 1)d]
Where:
- S<sub>n</sub> is the sum of the sequence (115 in our case).
- n is the number of terms in the sequence (2 in our case).
- a is the first term (which is x).
- d is the common difference (1 in our case).
Substituting the known values, we get:
115 = 2/2 * [2a + (2 - 1)1]
Simplifying this equation leads us to:
115 = 2a + 1
Solving for a:
114 = 2a a = 57
Again, we find that the first number is 57, and the second is 58. This approach demonstrates the connection between arithmetic sequences and consecutive integer problems.
Expanding the Problem: Generalizing the Solution
Let's generalize the problem. Instead of 115, let's use a variable, S, to represent the sum of two consecutive integers. We can then adapt the algebraic approach:
x + (x + 1) = S
Solving for x:
2x + 1 = S 2x = S - 1 x = (S - 1) / 2
This formula allows us to find the first of two consecutive integers whose sum is S. The second integer will simply be x + 1 = (S - 1) / 2 + 1 = (S + 1) / 2. This is a powerful tool; you can now quickly find consecutive integers that sum to any given number.
Extending the Concept: More Than Two Consecutive Numbers
What if we wanted to find three consecutive numbers whose sum is 115? Let's use the algebraic approach again:
x + (x + 1) + (x + 2) = 115
Solving for x:
3x + 3 = 115 3x = 112 x = 37.333...
Notice that x is not an integer. This means there are no three consecutive integers whose sum is 115. This highlights the importance of carefully considering the constraints of the problem. The solution might not always exist, depending on the parameters.
What if the numbers aren't consecutive?
Let's modify the problem: find two numbers that differ by 5 and have a sum of 115. We can still use algebra:
x + (x + 5) = 115
Solving for x:
2x + 5 = 115 2x = 110 x = 55
Therefore, the two numbers are 55 and 60. This shows the adaptability of the algebraic approach to various problem variations.
Frequently Asked Questions (FAQ)
-
Q: Can this method be used for larger numbers? A: Absolutely! The algebraic method and the generalized formula work for any sum of consecutive numbers, regardless of size.
-
Q: What if the numbers are negative? A: The algebraic methods still apply. Negative numbers simply follow the same rules of addition and subtraction.
-
Q: Are there other ways to solve this problem? A: While the methods discussed here are the most efficient, other approaches, like using a computer program or visual representation, are possible. However, these methods often lack the elegance and educational value of the approaches described above.
-
Q: What are the real-world applications of solving this type of problem? A: While this specific problem might not seem directly applicable to everyday life, the underlying principles of problem-solving and algebraic thinking are crucial in various fields like engineering, finance, and computer science. The ability to break down complex problems into simpler, solvable components is a highly valuable skill.
Conclusion: Beyond the Numbers
This seemingly simple problem of finding two consecutive numbers whose sum is 115 has led us on a journey through various mathematical concepts and problem-solving strategies. We've seen the power of intuition, the rigor of algebra, and the elegance of mathematical formulas. More importantly, this exercise has highlighted the importance of developing a systematic approach to problem-solving, a skill that extends far beyond the realm of mathematics and is invaluable in all aspects of life. The ability to generalize solutions and adapt methods to different scenarios is a key takeaway, empowering you to tackle more complex mathematical challenges with confidence and competence. Remember, mathematics is not just about finding the answer; it's about understanding the process and developing the skills to solve any problem that comes your way.
Latest Posts
Latest Posts
-
How Do You Learn The Best
Sep 15, 2025
-
How Long Is 25 Miles In A Car
Sep 15, 2025
-
Whats The Measurement Of A Triangle
Sep 15, 2025
-
Does A Plant Cell Have A Chromatin
Sep 15, 2025
-
How To Find Position From Velocity Graph
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Find Two Consecutive Numbers Whose Sum Is 115 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.