Find Three Consecutive Integers Whose Sum Is 36
faraar
Sep 07, 2025 · 5 min read
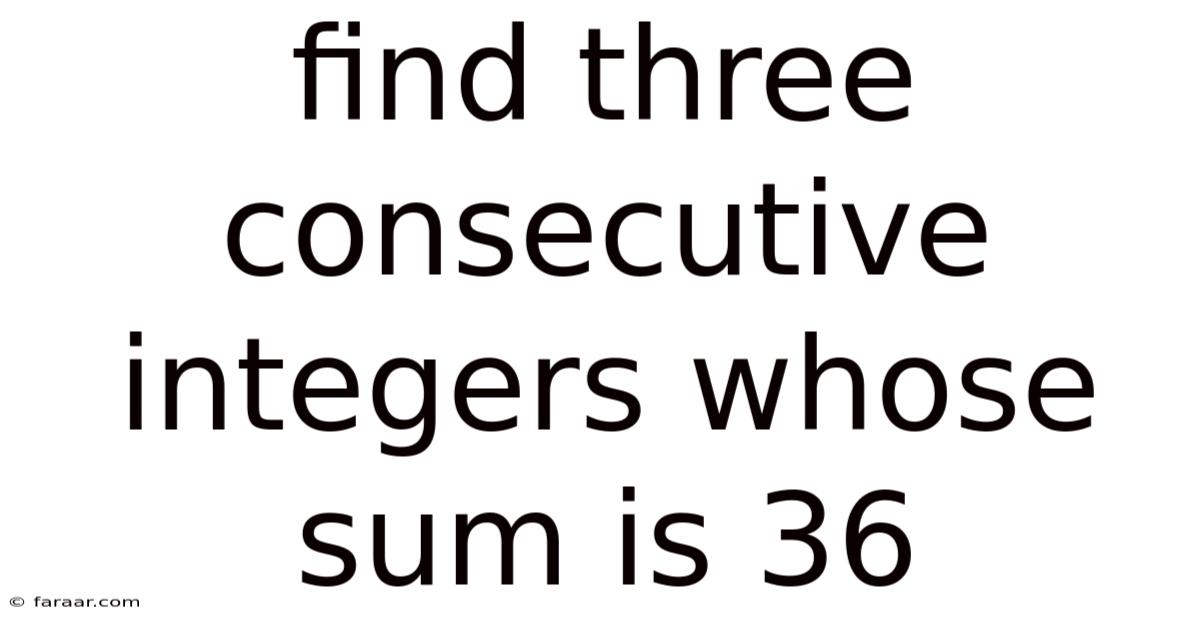
Table of Contents
Finding Three Consecutive Integers that Sum to 36: A Deep Dive into Problem Solving
This article explores the seemingly simple problem of finding three consecutive integers that add up to 36. While the solution might appear straightforward at first glance, we'll delve into multiple approaches to solving this, highlighting different mathematical concepts and problem-solving strategies. This will not only provide the answer but also equip you with valuable tools for tackling similar problems in the future. Understanding this problem opens doors to more complex mathematical explorations involving sequences, series, and algebraic equations.
Understanding the Problem
The core of the problem lies in defining "consecutive integers." Consecutive integers are whole numbers that follow each other in order, with a difference of 1 between each number. For example, 1, 2, and 3 are consecutive integers, as are -5, -4, and -3. Our task is to find three such integers whose sum is exactly 36.
Method 1: The Intuitive Approach
Let's start with an intuitive approach. We can reason that if we have three numbers that are roughly equal and add up to 36, each number must be approximately 36 / 3 = 12. Therefore, we can test integers around 12:
- Let's try 11, 12, and 13. Their sum is 11 + 12 + 13 = 36. We have found our solution!
This approach works well for simple problems, but it's not always efficient or guaranteed to find a solution for more complex scenarios.
Method 2: The Algebraic Approach
This method uses algebraic equations to find a more robust and general solution. We can represent the three consecutive integers as:
- First integer: x
- Second integer: x + 1
- Third integer: x + 2
Their sum is given as 36, so we can write the equation:
x + (x + 1) + (x + 2) = 36
Now, we solve for x:
- Combine like terms: 3x + 3 = 36
- Subtract 3 from both sides: 3x = 33
- Divide both sides by 3: x = 11
Therefore, the first integer is 11. The consecutive integers are 11, 12, and 13, confirming our solution from the intuitive approach.
Method 3: The Arithmetic Sequence Approach
This problem can also be viewed through the lens of arithmetic sequences. An arithmetic sequence is a sequence of numbers where the difference between consecutive terms is constant. In our case, the common difference is 1. The sum of an arithmetic sequence can be calculated using the formula:
S = (n/2) * [2a + (n-1)d]
Where:
- S is the sum of the sequence (36 in our case)
- n is the number of terms (3 in our case)
- a is the first term (x in our case)
- d is the common difference (1 in our case)
Substituting our values:
36 = (3/2) * [2x + (3-1)*1]
Simplifying:
36 = (3/2) * [2x + 2] 72 = 6x + 6 66 = 6x x = 11
Again, we find that the first integer is 11, leading to the same solution: 11, 12, and 13.
Expanding the Problem: Generalizing the Solution
Let's generalize this to find n consecutive integers whose sum is S. Using the arithmetic sequence formula:
S = (n/2) * [2a + (n-1)d]
If we have n consecutive integers, the common difference d will always be 1. So the formula simplifies to:
S = (n/2) * [2a + (n-1)]
We can rearrange this formula to solve for the first term, a:
2S = n[2a + (n-1)] 2S/n = 2a + n -1 2S/n - n + 1 = 2a a = (2S/n - n + 1) / 2
This formula allows us to find the first term of any sequence of n consecutive integers that sum to S. For our original problem (S=36, n=3):
a = (2*36/3 - 3 + 1) / 2 = (24 - 2) / 2 = 11
This confirms our previous results.
Exploring Variations: Even and Odd Consecutive Integers
Let's explore variations of this problem. What if we were asked to find three consecutive even integers whose sum is 36? We can modify our algebraic approach:
- First integer: x
- Second integer: x + 2
- Third integer: x + 4
The equation becomes:
x + (x + 2) + (x + 4) = 36
Solving this equation:
3x + 6 = 36 3x = 30 x = 10
The three consecutive even integers are 10, 12, and 14.
Similarly, for three consecutive odd integers:
- First integer: x
- Second integer: x + 2
- Third integer: x + 4
The equation remains the same, leading to the same solution: 10, 12, and 14. Note that although we solved for consecutive odd integers, the solution contains only even numbers. This highlights that the structure of consecutive even or odd numbers still has a constant difference of 2.
Frequently Asked Questions (FAQ)
Q1: Can this problem be solved using other methods?
A1: Yes, there are several other approaches, including graphical methods (plotting the sums of consecutive integers) and programming techniques (iterating through integers and checking the sum).
Q2: What if the sum wasn't 36? How would the solution change?
A2: The algebraic and arithmetic sequence approaches provide general solutions. Simply substitute the new sum value into the equations, and solve for x.
Q3: Are there always three consecutive integers that sum to a given number?
A3: No. Only numbers divisible by 3 can be expressed as the sum of three consecutive integers. For example, there are no three consecutive integers that sum to 25.
Q4: How can I apply this to more complex problems?
A4: The principles of algebraic manipulation and arithmetic sequences are widely applicable. You can adapt these methods to solve problems involving more integers, different common differences, or even more complex series.
Conclusion
Finding three consecutive integers that sum to 36 is a seemingly simple problem, yet it provides a fertile ground for exploring various mathematical concepts and problem-solving techniques. We’ve examined intuitive, algebraic, and arithmetic sequence approaches, highlighting their strengths and limitations. Furthermore, we've generalized the solution to find n consecutive integers that sum to a given number S, demonstrating the power of mathematical abstraction. By understanding these different methods, you develop a more versatile and robust problem-solving toolkit, enabling you to tackle more complex mathematical challenges with greater confidence. The journey of solving this problem is as valuable as the solution itself, fostering a deeper understanding of fundamental mathematical principles and enhancing your problem-solving skills.
Latest Posts
Latest Posts
-
Use The Graph To Write An Equation For The Parabola
Sep 08, 2025
-
Fast Ways To Win In Chess
Sep 08, 2025
-
Find The Value Of X That Makes The Lines Parallel
Sep 08, 2025
-
Why Is New York Not Part Of New England
Sep 08, 2025
-
2 1 4 Cups Divided By 3
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Find Three Consecutive Integers Whose Sum Is 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.