Find The Number That Makes The Ratio Equivalent To 1:6.
faraar
Sep 23, 2025 · 6 min read
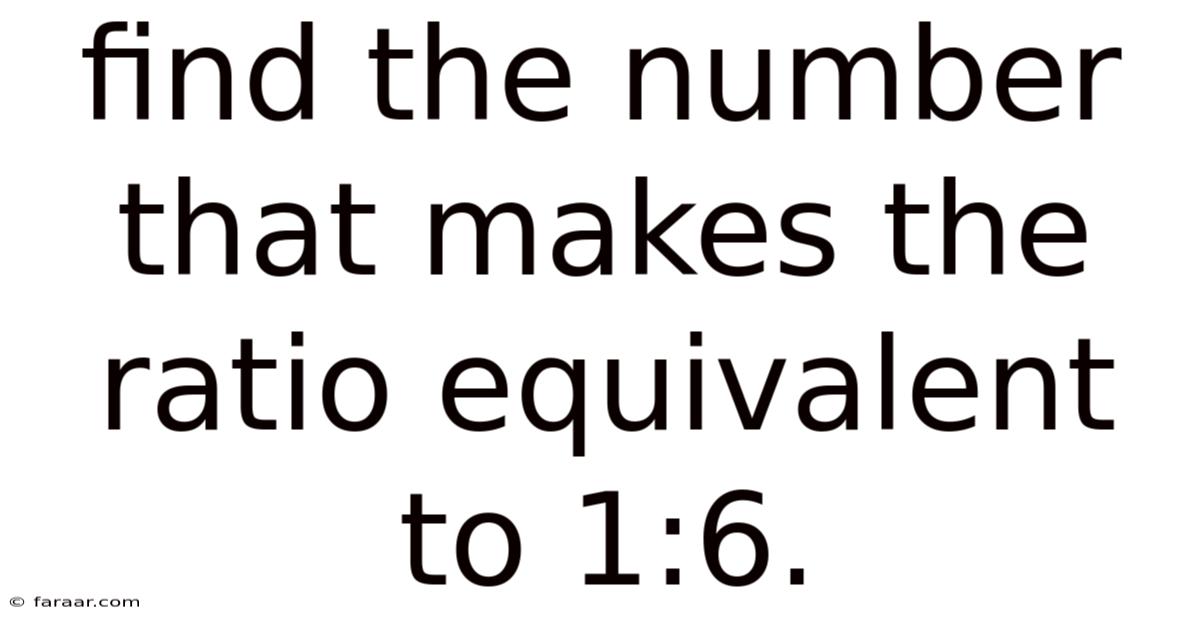
Table of Contents
Finding the Missing Number in Equivalent Ratios: A Comprehensive Guide to 1:6
Understanding ratios and proportions is fundamental in various fields, from cooking and construction to advanced mathematics and scientific research. This article delves into the process of finding a missing number to create an equivalent ratio to 1:6. We'll explore the underlying concepts, provide step-by-step instructions, delve into the mathematical principles, and address frequently asked questions to ensure a comprehensive understanding. This guide aims to equip you with the skills to confidently tackle similar ratio problems.
Introduction to Ratios and Proportions
A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. We often express ratios using colons (e.g., 1:6) or as fractions (e.g., 1/6). A ratio of 1:6 means that for every one unit of the first quantity, there are six units of the second quantity.
A proportion is a statement that two ratios are equal. For example, 1:6 = x:36 is a proportion. Finding a missing number in a proportion involves determining the value of the unknown variable that makes the ratios equivalent. In essence, we're scaling up or down the ratio while maintaining the same relationship between the quantities.
Step-by-Step Guide to Finding the Equivalent Ratio
Let's consider the problem: Find the number that makes the ratio equivalent to 1:6. This is an incomplete proportion. Let's represent the unknown number with 'x'. We can express this as:
1:6 = x:y (where 'y' represents the second number in the second ratio)
To find the missing number, we'll use the concept of cross-multiplication.
Step 1: Set up the Proportion
First, we need to set up the proportion. Let's assume we want to find the missing number that makes the ratio equivalent to 1:6 when the second number is 36. Our proportion becomes:
1/6 = x/36
Step 2: Cross-Multiply
Cross-multiply the terms diagonally:
1 * 36 = 6 * x
This simplifies to:
36 = 6x
Step 3: Solve for x
Now, we solve for x by isolating it on one side of the equation. Divide both sides of the equation by 6:
36/6 = 6x/6
This simplifies to:
x = 6
Therefore, the number that makes the ratio 6:36 equivalent to 1:6 is 6.
Let's try another example: Find the number that makes the ratio equivalent to 1:6, where the first number is 12. This time, our proportion is:
1/6 = 12/y
Step 1: Set up the Proportion
1/6 = 12/y
Step 2: Cross-Multiply
1 * y = 6 * 12
This simplifies to:
y = 72
Therefore, the ratio 12:72 is equivalent to 1:6.
Mathematical Explanation: Scaling and Proportionality
The method of cross-multiplication is a direct application of the principle of proportionality. When we have two equivalent ratios, a/b = c/d, it implies that the relationship between 'a' and 'b' is the same as the relationship between 'c' and 'd'. This relationship is a constant scaling factor. We can express this as:
a = kb and c = kd
where 'k' is the constant of proportionality.
Cross-multiplication essentially eliminates 'k' and allows us to solve for the unknown variable. In our example, 1/6 = x/36, the constant of proportionality is 6 (because 6 * 1 = 6 and 6 * 6 = 36).
Different Scenarios and Problem-Solving Strategies
The process remains the same even if the unknown variable is in a different position in the proportion. For instance, if the problem is presented as:
x:6 = 3:18
We still apply the cross-multiplication method:
18x = 18
x = 1
Or consider a scenario where we are given a ratio with larger numbers:
15:x = 5:12
Cross-multiplying:
15 * 12 = 5x
180 = 5x
x = 36
The key is to always set up the proportion correctly, ensuring that corresponding quantities are in the same position in both ratios.
Real-World Applications of Equivalent Ratios
The concept of equivalent ratios is widely used in various real-world scenarios. Here are a few examples:
-
Recipe Scaling: If a recipe calls for a 1:6 ratio of sugar to flour, you can use equivalent ratios to scale the recipe up or down to accommodate a different number of servings.
-
Map Scales: Maps use ratios to represent distances on the ground. Understanding equivalent ratios helps determine actual distances based on measurements on the map.
-
Unit Conversions: Converting units (e.g., miles to kilometers, liters to gallons) involves using equivalent ratios.
-
Finance: Calculating interest rates, proportions of investments, and comparing financial data frequently involves working with ratios and proportions.
-
Science: Many scientific principles and calculations rely on understanding ratios and proportions, from chemical reactions to physics calculations.
Frequently Asked Questions (FAQ)
Q1: What happens if I get a decimal or fraction as a result?
A1: Getting a decimal or fraction as a result is perfectly acceptable. Ratios often involve non-whole numbers. For example, if you find x = 2.5 or x = 1/3, these are valid solutions.
Q2: Can I solve these problems without cross-multiplication?
A2: Yes, you can solve these problems using other methods. One approach is to find the scaling factor. For example, in the ratio 1:6 = x:36, you can see that 36 is 6 times larger than 6. Therefore, you multiply 1 by 6 to find x (which is 6). This method requires recognizing the relationship between the numbers, while cross-multiplication provides a more systematic approach that works even when the relationships aren't immediately obvious.
Q3: What if I have more than two ratios in a proportion?
A3: Proportions typically involve two ratios. However, you might encounter problems with more complex relationships. In such cases, the fundamental principle remains the same – you must maintain the proportionality between the quantities. You can often break down the complex proportion into simpler proportions that you can solve individually.
Q4: Are there any online tools or calculators to help solve ratio problems?
A4: While there are various online calculators available for ratios and proportions, understanding the underlying mathematical principles is essential. Calculators can be helpful for checking your work, but it is crucial to develop your problem-solving skills.
Conclusion
Finding the missing number in equivalent ratios, such as finding the number that makes a ratio equivalent to 1:6, involves understanding and applying the concept of proportions. The method of cross-multiplication offers a straightforward and reliable way to solve these problems. By mastering this technique and understanding the underlying principles of proportionality, you can confidently tackle various ratio problems in diverse fields. Remember to always focus on setting up the proportion correctly and carefully executing the algebraic steps to arrive at the accurate solution. Practice makes perfect, so keep practicing and you'll soon become proficient in handling ratio problems.
Latest Posts
Latest Posts
-
The Quotient Of A Number And 4 Is 7
Sep 23, 2025
-
1 3 Cup Twice Is How Much
Sep 23, 2025
-
How Much Cashews At 1 58 Per Pound
Sep 23, 2025
-
Find X Such That The Matrix Is Singular
Sep 23, 2025
-
V E N I In English
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Find The Number That Makes The Ratio Equivalent To 1:6. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.