Factors Of -36 That Add Up To -5
faraar
Sep 18, 2025 · 5 min read
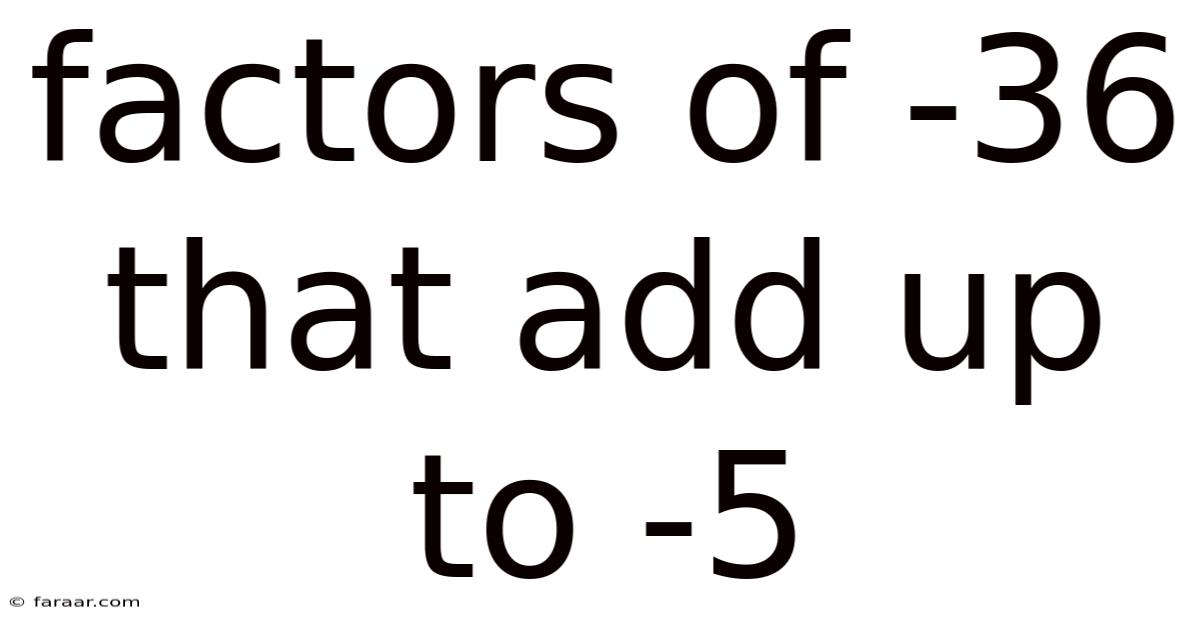
Table of Contents
Finding Factors of -36 that Add Up to -5: A Deep Dive into Number Theory
Finding factors of a number that add up to a specific sum is a common problem in algebra, particularly when dealing with factoring quadratic expressions and solving equations. This article will explore the process of identifying the factors of -36 that add up to -5, providing a detailed explanation suitable for learners of various mathematical backgrounds. We will delve into the underlying principles of number theory, offering practical steps and illustrating the solution with multiple approaches.
Introduction
The problem at hand involves finding two numbers that, when multiplied, result in -36 and, when added, result in -5. This problem is crucial for understanding factoring techniques used in solving quadratic equations and simplifying algebraic expressions. The core concepts involve understanding factors, integers, and the relationships between multiplication and addition. We will explore different methods to solve this, from systematic listing to employing algebraic reasoning.
Understanding Factors and Integers
Before we begin, let's clarify some fundamental terms. Factors are numbers that divide exactly into another number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. Integers are whole numbers, including positive and negative numbers (e.g., ...-3, -2, -1, 0, 1, 2, 3...). In our problem, we're looking for integer factors of -36.
The fact that our target product is -36 means one factor must be positive and the other negative. This is because a negative number is the result of multiplying a positive and a negative number.
Method 1: Systematic Listing and Trial and Error
The most straightforward approach is to systematically list all the factor pairs of -36 and check their sums. Remember that the pairs will consist of one positive and one negative factor:
- (-1, 36): -1 + 36 = 35
- (-2, 18): -2 + 18 = 16
- (-3, 12): -3 + 12 = 9
- (-4, 9): -4 + 9 = 5
- (-6, 6): -6 + 6 = 0
- (-9, 4): -9 + 4 = -5
- (-12, 3): -12 + 3 = -9
- (-18, 2): -18 + 2 = -16
- (-36, 1): -36 + 1 = -35
From this list, we find that the pair -9 and 4 satisfies both conditions: (-9) * 4 = -36 and -9 + 4 = -5.
Method 2: Using Algebraic Reasoning
A more sophisticated approach involves setting up an algebraic equation. Let's represent the two factors as 'x' and 'y'. We know that:
- x * y = -36
- x + y = -5
We can solve this system of equations. From the second equation, we can express one variable in terms of the other: y = -5 - x. Substituting this into the first equation gives:
x * (-5 - x) = -36
Expanding and rearranging this equation, we get a quadratic equation:
x² + 5x - 36 = 0
This quadratic equation can be solved using various methods, including factoring, the quadratic formula, or completing the square. Factoring is the most efficient method in this case:
(x + 9)(x - 4) = 0
This gives us two possible solutions for x: x = -9 or x = 4.
- If x = -9, then y = -5 - (-9) = 4
- If x = 4, then y = -5 - 4 = -9
Therefore, the two factors are -9 and 4.
Method 3: Understanding the Relationship Between Sums and Products
This method leverages a deeper understanding of the relationship between the sum and product of the factors. Consider a general quadratic expression of the form:
x² + bx + c = 0
When we factor this quadratic expression into (x + p)(x + q), we know that:
- p * q = c (the product of the roots)
- p + q = b (the sum of the roots)
In our case, we have the product (-36) and the sum (-5). We are essentially looking for two numbers whose product is -36 and sum is -5. This directly connects to finding the roots of the quadratic equation x² - 5x - 36 = 0, which is equivalent to the algebraic method described above.
Further Applications and Extensions
The ability to find factors that add up to a certain sum has wide-ranging applications in mathematics and beyond. Some key areas include:
- Factoring Quadratic Expressions: This is perhaps the most direct application. Understanding this concept is fundamental to simplifying algebraic expressions and solving quadratic equations.
- Solving Word Problems: Many word problems involving areas, products, and sums can be modeled using quadratic equations, requiring the ability to find factors with specific sums.
- Number Theory: This problem falls under number theory, a branch of mathematics concerned with the properties of integers. Exploring factor pairs and their relationships is a cornerstone of this field.
- Computer Programming: Algorithms for finding factors are used in various computer programs, especially in cryptography and optimization problems.
Frequently Asked Questions (FAQ)
-
Q: Are there other pairs of factors for -36?
- A: Yes, many pairs of factors exist for -36. However, only the pair -9 and 4 adds up to -5.
-
Q: What if the sum was a different number?
- A: The process remains the same. You would systematically list the factor pairs or use the algebraic approach to find the pair with the required sum.
-
Q: What if the target number was positive instead of negative?
- A: If the target product was positive, both factors would either be positive or both negative. The approach to finding the pair with the correct sum would be similar, but the signs of the factors would change accordingly.
-
Q: Can this method be applied to numbers other than -36?
- A: Absolutely! This method applies to any number where you need to find factors that satisfy a given sum.
Conclusion
Finding the factors of -36 that add up to -5 is a problem that reinforces fundamental concepts in algebra and number theory. We've explored three different approaches: systematic listing, algebraic reasoning, and a more intuitive method leveraging the relationship between the sum and product of factors. Each method offers valuable insights into the problem, showcasing different mathematical techniques. Mastering this skill builds a strong foundation for tackling more complex algebraic problems and strengthens your understanding of number theory. The core takeaway is the interplay between multiplication and addition, a crucial relationship across various mathematical domains. Remember that practice is key – the more you work with factor pairs, the more intuitive this process will become.
Latest Posts
Latest Posts
-
How Do You Find The Decay Factor
Sep 19, 2025
-
What Is The Slope Of A Velocity Vs Time Graph
Sep 19, 2025
-
If Is A Linear Transformation Such That Then
Sep 19, 2025
-
Is Amu The Same As G Mol
Sep 19, 2025
-
How Do You Find The Volume In Cubic Centimeters
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Factors Of -36 That Add Up To -5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.