Evaluate A 2 B 2 For A 4 And B
faraar
Sep 21, 2025 · 6 min read
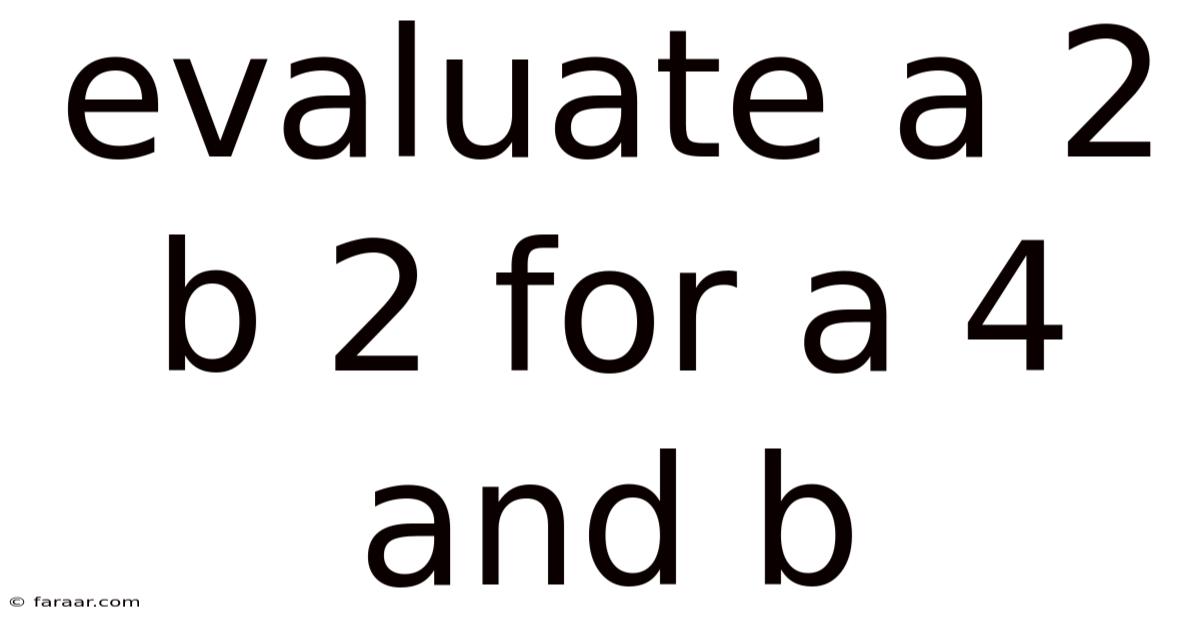
Table of Contents
Evaluating a²b² for a = 4 and b = ? Unlocking the Power of Algebraic Substitution
This article delves into the process of evaluating algebraic expressions, specifically focusing on the expression a²b². We'll explore how to substitute given values for variables, perform the necessary calculations, and understand the underlying mathematical principles. This comprehensive guide is designed to provide a clear understanding of the concept, suitable for students of various mathematical backgrounds, from beginners to those seeking a deeper understanding. We will not only solve the problem for a specific value of 'a' but also examine how the expression behaves with different values for 'b', emphasizing the importance of understanding variable relationships.
Understanding Algebraic Expressions
Before we dive into evaluating a²b², let's establish a foundational understanding of algebraic expressions. An algebraic expression is a mathematical phrase that combines numbers, variables, and operators (like +, -, ×, ÷). Variables, usually represented by letters (like a, b, x, y), represent unknown quantities or values that can change. The expression a²b² contains two variables, a and b, raised to powers and multiplied together. The superscript '2' indicates that each variable is squared (multiplied by itself).
Substituting Values into the Expression
The core of evaluating an algebraic expression lies in the process of substitution. This involves replacing the variables with their given numerical values and then performing the arithmetic operations according to the order of operations (PEMDAS/BODMAS). In our case, we are given that a = 4. We are not given a specific value for b, which means our final answer will be an expression in terms of b.
Step-by-Step Evaluation for a = 4
Let's substitute a = 4 into the expression a²b²:
-
Replace 'a' with 4: The expression becomes (4)²b².
-
Square the value of 'a': (4)² = 4 × 4 = 16. The expression now simplifies to 16b².
-
Final Expression: The evaluated expression for a = 4 is 16b². This is as far as we can simplify without a numerical value for b.
Exploring Different Values of 'b'
Now let's explore how the expression 16b² changes with different values of b. This demonstrates the dynamic nature of algebraic expressions and the impact of changing variable values.
- If b = 1: 16(1)² = 16 × 1 = 16.
- If b = 2: 16(2)² = 16 × 4 = 64.
- If b = 3: 16(3)² = 16 × 9 = 144.
- If b = 0: 16(0)² = 16 × 0 = 0.
- If b = -1: 16(-1)² = 16 × 1 = 16.
- If b = -2: 16(-2)² = 16 × 4 = 64.
As you can see, the value of the expression 16b² changes dramatically depending on the value assigned to b. The expression is a quadratic function of b, meaning it follows a parabolic curve when graphed. This highlights the importance of considering the impact of all variables within an expression.
The Significance of Order of Operations (PEMDAS/BODMAS)
The order of operations is crucial when evaluating algebraic expressions. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) provides a standardized sequence for performing calculations. In our example, the exponent (squaring) is performed before the multiplication (multiplying by b²). Ignoring the order of operations would lead to incorrect results.
Understanding the Concept of Variables and Constants
In the expression a²b², a and b are variables, representing quantities that can take on different values. The number '2' in a² and b² is a constant, its value remains unchanged throughout the evaluation process. Understanding the distinction between variables and constants is essential for effectively working with algebraic expressions.
Expanding the Concept: More Complex Expressions
Let's consider a slightly more complex expression involving a and b: 2a³ + 3b² - 5ab. Let's evaluate this expression for a = 4 and b = 2:
-
Substitute values: 2(4)³ + 3(2)² - 5(4)(2)
-
Calculate exponents: 2(64) + 3(4) - 5(4)(2)
-
Perform multiplication: 128 + 12 - 40
-
Perform addition and subtraction: 100
Therefore, the value of 2a³ + 3b² - 5ab for a = 4 and b = 2 is 100. This example showcases the application of the same principles to more complex algebraic expressions. Each term is evaluated separately, then the results are combined based on the operators (+, -, ×, ÷).
Practical Applications of Algebraic Expressions
Evaluating algebraic expressions is a fundamental skill with wide-ranging applications in various fields:
-
Physics: Calculating forces, velocities, accelerations, and other physical quantities often involves using algebraic expressions.
-
Engineering: Designing structures, circuits, and other engineering systems requires manipulating and evaluating algebraic expressions to ensure functionality and safety.
-
Computer Science: Programming and software development rely heavily on algebraic expressions to represent algorithms and perform calculations.
-
Economics and Finance: Modeling economic trends, forecasting financial markets, and calculating investment returns all involve working with algebraic expressions.
-
Statistics: Statistical analysis frequently uses algebraic expressions to summarize data, perform hypothesis testing, and build statistical models.
Frequently Asked Questions (FAQ)
-
Q: What happens if 'b' is a negative number?
A: When b is negative, the value of 16b² will still be positive because squaring a negative number results in a positive number. For example, if b = -3, then 16b² = 16(-3)² = 16(9) = 144.
-
Q: Can I evaluate the expression if only 'b' is given?
A: No. The expression a²b² contains two variables, a and b. You need the numerical value for both variables to calculate a single numerical result. If only 'b' is given, you can only simplify the expression to a form containing 'a'.
-
Q: What if the expression was (a+b)²?
A: This would require a different approach. You would first substitute the values of a and b, then perform the addition within the parentheses before squaring the result. For a = 4 and b = 2, (a+b)² = (4+2)² = 6² = 36.
-
Q: Is there a way to visualize the behavior of the expression 16b²?
A: Yes, you can graph the expression as a function of b. The graph will be a parabola opening upwards, illustrating the quadratic relationship between b and the value of the expression.
Conclusion
Evaluating algebraic expressions like a²b² involves a systematic process of substitution, followed by the careful application of the order of operations. Understanding the role of variables and constants, and the impact of different numerical values on the final result is crucial. The ability to evaluate such expressions is a fundamental skill, extending far beyond the classroom and into various fields requiring mathematical problem-solving and quantitative analysis. Remember, practice is key to mastering this skill. By working through numerous examples, you'll build confidence and become proficient in evaluating increasingly complex algebraic expressions.
Latest Posts
Latest Posts
-
What Is The Gcf Of 8
Sep 21, 2025
-
Find The Missing Side In The Similar Figures Below
Sep 21, 2025
-
Is Tarnishing A Physical Or Chemical Change
Sep 21, 2025
-
How Many Neutrons Are Needed To Initiate The Fission Reaction
Sep 21, 2025
-
What Is One Third Of One Half
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Evaluate A 2 B 2 For A 4 And B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.