Dy Dx X 2 Y 2
faraar
Aug 25, 2025 · 7 min read
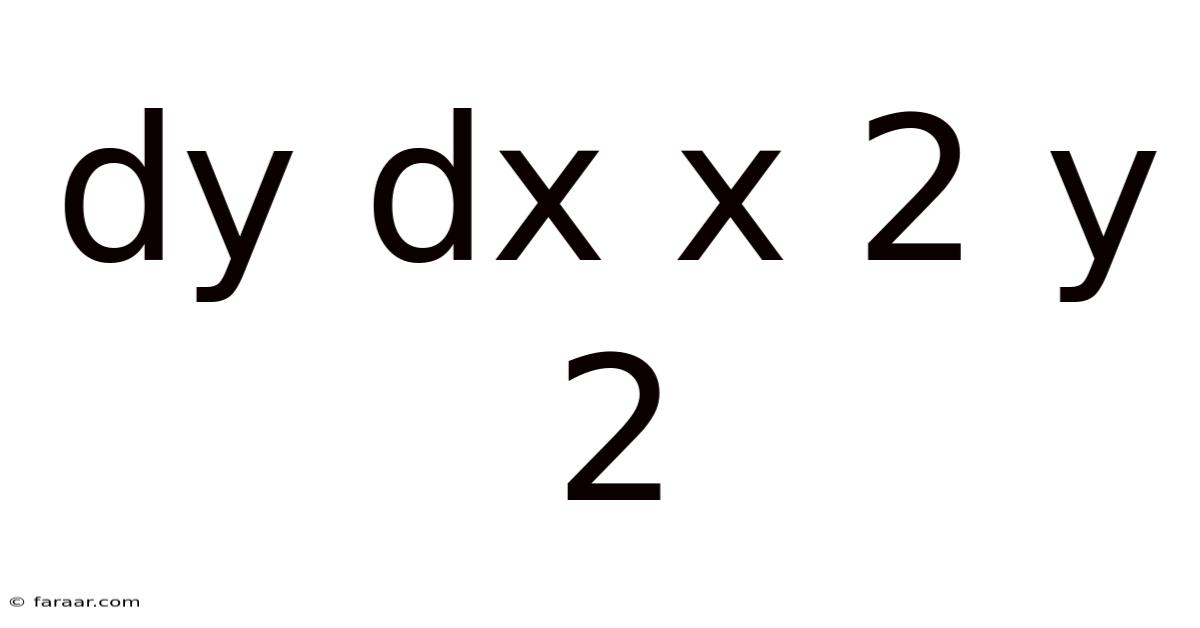
Table of Contents
Unveiling the Mysteries of dy/dx = x² + y²: A Deep Dive into Differential Equations
The equation dy/dx = x² + y² represents a fascinating challenge in the realm of differential equations. This seemingly simple expression hides a rich tapestry of mathematical concepts, demanding a blend of analytical techniques and numerical methods for its complete understanding. This article will explore this equation in detail, demystifying its properties and providing insights into its solutions. We'll delve into its classification, attempt analytical solutions where possible, and examine the role of numerical methods in tackling its complexities. Understanding this equation provides a solid foundation for tackling more advanced differential equations encountered in various scientific and engineering disciplines.
Introduction: Understanding the Equation's Nature
dy/dx = x² + y² is a first-order, nonlinear ordinary differential equation (ODE). Let's break down what this means:
- First-order: The equation involves only the first derivative of the dependent variable,
y, with respect to the independent variable,x. - Nonlinear: The presence of the
y²term makes the equation nonlinear. Linear ODEs have a simpler structure and often admit closed-form analytical solutions. Nonlinear ODEs are generally much more challenging to solve analytically. - Ordinary differential equation (ODE): The equation involves only ordinary derivatives, meaning that the derivatives are with respect to a single independent variable (
xin this case). Partial differential equations (PDEs) involve derivatives with respect to multiple independent variables.
The nonlinearity of dy/dx = x² + y² significantly complicates the search for an analytical solution. Unlike many linear ODEs, we cannot expect a neat, closed-form expression for y(x). This necessitates the exploration of alternative solution techniques, primarily numerical methods.
Attempts at Analytical Solutions: Limitations and Insights
While a complete analytical solution for dy/dx = x² + y² is elusive, we can gain some insights by exploring various techniques. However, we will quickly encounter limitations stemming from the equation's nonlinearity.
One might initially consider using techniques like separation of variables or integrating factors, commonly employed for simpler first-order ODEs. However, these methods prove ineffective in this case due to the presence of both x² and y² terms which cannot be easily separated.
Let's attempt a power series approach. We assume a solution of the form:
y(x) = a₀ + a₁x + a₂x² + a₃x³ + ...
Substituting this into the original equation and comparing coefficients of like powers of x leads to a system of recursive relations for the coefficients aᵢ. This approach, while potentially leading to an approximate solution, becomes computationally intensive and doesn't provide a closed-form expression. Furthermore, the convergence of such a series is not guaranteed over the entire domain.
Numerical Methods: Approximating Solutions
Given the difficulty in finding an analytical solution, we turn to numerical methods to approximate the solution of dy/dx = x² + y². Several methods are available, each with its strengths and limitations:
- Euler's Method: This is a simple yet fundamental method. It approximates the solution by iteratively applying the formula:
yᵢ₊₁ = yᵢ + h*f(xᵢ, yᵢ)
where h is the step size, f(xᵢ, yᵢ) = xᵢ² + yᵢ², and yᵢ is the approximation of y(xᵢ). Euler's method is relatively easy to implement but can suffer from significant inaccuracies, especially with large step sizes.
- Improved Euler Method (Heun's Method): This method enhances accuracy by averaging the slopes at the beginning and end of each step:
k₁ = h*f(xᵢ, yᵢ)
k₂ = h*f(xᵢ + h, yᵢ + k₁)
yᵢ₊₁ = yᵢ + (k₁ + k₂)/2
Heun's method provides a more accurate approximation than Euler's method for the same step size.
-
Runge-Kutta Methods: These are a family of higher-order methods known for their accuracy and efficiency. The most popular is the fourth-order Runge-Kutta method (RK4), which uses a weighted average of slopes at different points within each step. RK4 offers significantly improved accuracy compared to Euler's method and Heun's method. The formulas involved are more complex but readily available in numerical analysis textbooks and software libraries.
-
Other Advanced Methods: More sophisticated techniques such as predictor-corrector methods, multistep methods, and adaptive step-size methods can further enhance accuracy and efficiency. The choice of method depends on the desired level of accuracy and computational resources.
Implementing Numerical Methods: A Practical Example
Let's consider a simple implementation of Euler's method using Python:
def euler_method(f, x0, y0, h, n):
x_values = [x0 + i*h for i in range(n+1)]
y_values = [y0]
for i in range(n):
y_next = y_values[-1] + h*f(x_values[i], y_values[-1])
y_values.append(y_next)
return x_values, y_values
# Define the function f(x, y) = x² + y²
def f(x, y):
return x**2 + y**2
# Initial conditions and parameters
x0 = 0
y0 = 1
h = 0.1
n = 10
# Apply Euler's method
x, y = euler_method(f, x0, y0, h, n)
# Print the results
for i in range(len(x)):
print(f"x = {x[i]:.1f}, y ≈ {y[i]:.4f}")
This code provides a basic implementation of Euler's method. For more accurate results, higher-order methods like RK4 should be used. Numerical solutions obtained using these methods can then be visualized graphically to understand the behavior of the solution curve.
Phase Plane Analysis: Visualizing the Solution
Phase plane analysis provides a powerful tool for understanding the qualitative behavior of solutions to differential equations, even without explicitly finding the solutions. For the equation dy/dx = x² + y², we can create a phase portrait by plotting the vector field defined by the equation. Each point (x, y) in the plane has a vector associated with it, whose direction is given by the slope dy/dx = x² + y² and magnitude is determined by the length of the vector.
Visualizing this vector field reveals interesting insights into the solution's behavior. The solutions will generally diverge rapidly, indicating exponential growth in y as x increases. The phase portrait provides a qualitative understanding of the solution's dynamics and is particularly useful when analytical solutions are unattainable.
Applications and Significance
Differential equations like dy/dx = x² + y², despite their seemingly simple form, appear in diverse scientific and engineering applications. While a specific real-world example directly modeled by this precise equation might be rare, it serves as a valuable prototype for understanding more complex nonlinear systems. Many nonlinear systems exhibit similar behaviors – rapid growth or oscillations – that can be studied through similar numerical and analytical techniques. Understanding this equation helps build the necessary mathematical intuition for analyzing and solving more complicated nonlinear ODEs frequently encountered in:
- Physics: Modeling population growth with nonlinear interactions, or describing certain types of damped or forced oscillations.
- Engineering: Analyzing circuits with nonlinear components or modeling the behavior of complex mechanical systems.
- Biology: Studying population dynamics under various growth conditions and resource constraints.
- Economics: Modeling economic systems where growth rates are not constant.
Frequently Asked Questions (FAQ)
Q1: Is there a closed-form solution to dy/dx = x² + y²?
A1: No, there's no known closed-form analytical solution to this nonlinear ODE. Numerical methods are necessary to approximate solutions.
Q2: Which numerical method is best for solving this equation?
A2: The optimal choice depends on the desired accuracy and computational resources. Higher-order methods like RK4 generally provide better accuracy than simpler methods like Euler's method, but they require more computation.
Q3: How does the initial condition affect the solution?
A3: The initial condition y(x₀) = y₀ significantly influences the specific solution curve. Different initial conditions lead to different solution trajectories.
Q4: What are the limitations of numerical methods?
A4: Numerical methods provide approximations, not exact solutions. Accuracy depends on the step size and the method used. Numerical errors can accumulate, especially over long intervals.
Q5: Can this equation be linearized?
A5: No, a simple linearization around a specific point is not sufficient to capture the overall behavior of this nonlinear equation. The nonlinearity is inherent and crucial to the system's dynamics.
Conclusion
The equation dy/dx = x² + y² serves as a compelling illustration of the challenges and rewards inherent in solving nonlinear differential equations. While an analytical solution remains elusive, numerical methods provide effective tools for approximating solutions and understanding the equation's behavior. The exploration of this equation provides crucial foundational knowledge for tackling more complex nonlinear systems encountered in diverse scientific and engineering domains. Through a combination of analytical insights and numerical techniques, coupled with visualization tools like phase plane analysis, we can gain a profound understanding of the solution's dynamics and appreciate the richness concealed within this apparently simple mathematical expression. The journey into solving this equation underscores the power of combining various mathematical approaches to unravel the complexities of the physical and engineered world.
Latest Posts
Latest Posts
-
How To Write Complex Numbers In Standard Form
Aug 25, 2025
-
How Do You Find The Magnitude Of The Acceleration
Aug 25, 2025
-
J Is 14 Less Than 22
Aug 25, 2025
-
Homework 10 Projectile Motion And Quadratic Regression
Aug 25, 2025
-
Find The Value Of X In The Diagram
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about Dy Dx X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.