Do 2 1/3 Cups Equal 2/3
faraar
Sep 15, 2025 · 6 min read
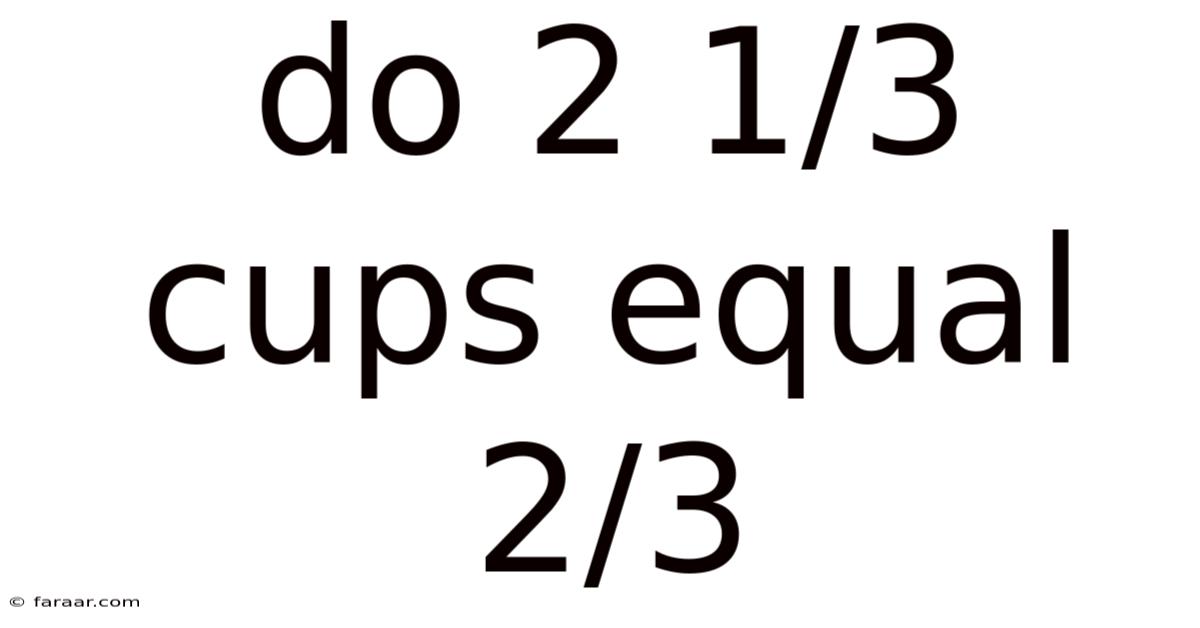
Table of Contents
Do 2 1/3 Cups Equal 2/3? Understanding Fractions and Measurement
This article will delve into the question: "Do 2 1/3 cups equal 2/3?" The answer, simply put, is no. Understanding why requires a grasp of fractions and their role in measurement. This seemingly simple question opens a door to exploring fundamental mathematical concepts crucial for everyday life, from cooking and baking to construction and scientific endeavors. We'll break down the concepts step-by-step, clarifying potential misunderstandings and solidifying your understanding of fractions and unit conversions.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's revisit the basics of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many parts we have, while the denominator tells us how many equal parts the whole is divided into.
For example, in the fraction 1/2 (one-half), the numerator is 1 (we have one part), and the denominator is 2 (the whole is divided into two equal parts). Similarly, in the fraction 2/3 (two-thirds), the numerator is 2 (we have two parts), and the denominator is 3 (the whole is divided into three equal parts).
Mixed Numbers and Improper Fractions
Our initial question involves a mixed number, which is a combination of a whole number and a fraction (2 1/3). A mixed number can be converted into an improper fraction, where the numerator is larger than or equal to the denominator. To convert 2 1/3 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 2 x 3 = 6
- Add the numerator to the result: 6 + 1 = 7
- Keep the same denominator: 3
Therefore, 2 1/3 is equivalent to the improper fraction 7/3.
Comparing Fractions: Finding Common Denominators
To compare 7/3 (our converted 2 1/3) and 2/3, we need a common denominator. This allows us to directly compare the numerators. In this case, both fractions already have the same denominator, 3. This simplifies the comparison significantly.
Because the numerators are 7 and 2 respectively, we can easily see that 7/3 is significantly larger than 2/3.
Visualizing the Difference
Imagine you have a pie. To represent 2/3, you'd cut the pie into three equal slices and take two of them. Now, imagine another pie. To represent 7/3, you'd need two whole pies and one additional slice from a third pie (because 7 divided by 3 is 2 with a remainder of 1). Clearly, 2/3 of a pie is much smaller than 2 1/3 pies.
The Importance of Units in Measurement
The question hinges not only on understanding fractions but also on the crucial role of units in measurement. The units "cups" are essential here. 2 1/3 cups signifies a specific volume. This volume is considerably larger than 2/3 of a cup. The units act as a crucial context, emphasizing that we're comparing volumes, not just abstract fractions.
Practical Applications: Cooking and Baking
Understanding fraction conversions is vital in cooking and baking. Recipes often call for precise measurements. Imagine a cake recipe that requires 2 1/3 cups of flour. If you mistakenly used only 2/3 of a cup, your cake would likely be a disaster! Accurate measurement is key to achieving the desired result.
Practical Applications: Construction and Engineering
In construction and engineering, precise measurements are paramount. Errors in fractions can lead to structural instability or malfunctioning machinery. From calculating the amount of concrete needed for a foundation to designing the precise dimensions of a bridge, the ability to accurately manipulate and compare fractions is non-negotiable.
Beyond Cups: Expanding to Other Units
The principle extends far beyond cups. Imagine working with meters, liters, or even smaller units like millimeters or microliters. The concept of fractions and their accurate manipulation remains the same. Accurate conversions between different units, combined with a firm grasp of fractions, ensures accuracy in various applications.
Mathematical Explanation: Converting Mixed Numbers to Improper Fractions
Let's reiterate the process of converting mixed numbers to improper fractions. This conversion is a fundamental step in comparing and performing calculations with fractions.
The general formula for converting a mixed number a b/c to an improper fraction is: (a * c + b) / c
Where:
- 'a' is the whole number part
- 'b' is the numerator of the fraction
- 'c' is the denominator of the fraction
Using our example: 2 1/3
- Multiply the whole number by the denominator: 2 * 3 = 6
- Add the numerator: 6 + 1 = 7
- Keep the denominator: 3
Therefore, 2 1/3 = 7/3
Mathematical Explanation: Comparing Fractions
Comparing fractions, especially when they don’t share the same denominator, requires finding a common denominator. In our case, it's already conveniently given to us: both 7/3 and 2/3 share the denominator 3. This allows for a direct comparison of their numerators.
Since 7 > 2, 7/3 > 2/3. Therefore, 2 1/3 cups is considerably greater than 2/3 of a cup.
Frequently Asked Questions (FAQ)
Q1: Can I always convert mixed numbers into improper fractions?
A1: Yes, absolutely! Converting to improper fractions simplifies calculations and comparisons, making them more straightforward.
Q2: Are there other ways to compare fractions besides finding a common denominator?
A2: Yes, you can use decimal equivalents. Converting fractions to decimals allows for easy comparison using decimal place values. For example, 7/3 ≈ 2.33 and 2/3 ≈ 0.67.
Q3: What if the fractions don’t have the same denominator?
A3: Find the least common multiple (LCM) of the denominators. This becomes the new common denominator. Then, multiply the numerator and denominator of each fraction by the necessary factor to achieve the common denominator. Only then can you accurately compare the fractions.
Q4: How important is accuracy in measurements, especially in cooking and baking?
A4: Accuracy in measurements is extremely important, especially in cooking and baking. Slight variations in ingredient amounts can significantly impact the final outcome, leading to a less-than-ideal result.
Q5: Are there any online tools or calculators that can help with fraction conversions?
A5: Yes, many online resources are available to assist with fraction conversions and calculations.
Conclusion: A Deeper Understanding of Fractions and Measurement
In conclusion, 2 1/3 cups absolutely do not equal 2/3 of a cup. This seemingly simple question highlighted the importance of understanding fractions, mixed numbers, improper fractions, and the crucial role of units in measurement. The difference is substantial, underlining the necessity of accuracy in various applications, from cooking and baking to engineering and construction. By understanding these fundamental concepts, you equip yourself with essential skills applicable to numerous aspects of life. The ability to accurately manipulate and compare fractions opens doors to problem-solving across a wide range of disciplines.
Latest Posts
Latest Posts
-
How To Solve Y 2x 3
Sep 15, 2025
-
127 Rounded To The Nearest Hundred
Sep 15, 2025
-
Calculate The Ph For Each Of The Following Solutions
Sep 15, 2025
-
Whats The Product Of 4 2 3 And 11 1 4
Sep 15, 2025
-
How To Find Moles Of Acetic Acid In Vinegar
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Do 2 1/3 Cups Equal 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.