Cot X Sin X Cos X
faraar
Sep 20, 2025 · 5 min read
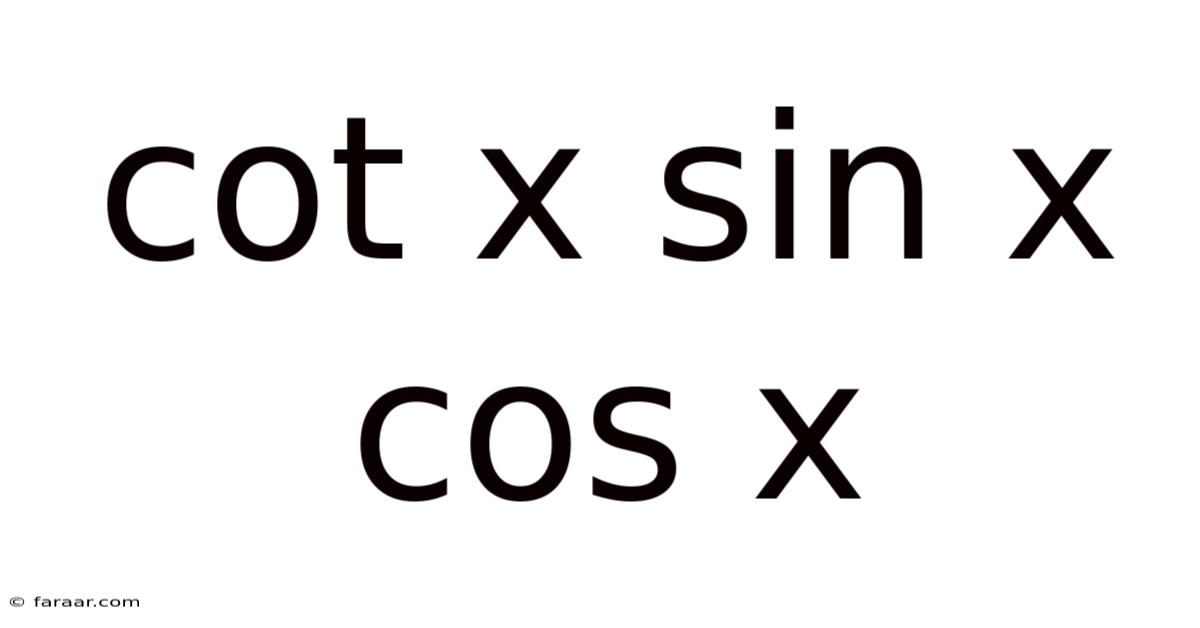
Table of Contents
Decoding the Trigonometric Expression: cot x sin x cos x
Understanding trigonometric identities and simplifying complex expressions is crucial in mathematics, particularly in calculus and physics. This article delves into the trigonometric expression cot x sin x cos x, exploring its simplification, applications, and deeper mathematical significance. We will break down the process step-by-step, ensuring even beginners can grasp the concepts involved. By the end, you'll not only be able to simplify this specific expression but also develop a stronger foundation in trigonometry.
Understanding the Components: cot x, sin x, and cos x
Before tackling the simplification, let's review the individual components:
-
cot x (cotangent of x): Defined as the ratio of cosine to sine,
cot x = cos x / sin x. It represents the reciprocal of the tangent function (tan x = sin x / cos x). -
sin x (sine of x): Represents the ratio of the length of the side opposite the angle x to the length of the hypotenuse in a right-angled triangle.
-
cos x (cosine of x): Represents the ratio of the length of the side adjacent to the angle x to the length of the hypotenuse in a right-angled triangle.
Step-by-Step Simplification of cot x sin x cos x
The key to simplifying this expression lies in substituting the definition of cotangent and then applying basic trigonometric rules. Here's the process:
-
Substitute the definition of cot x: We begin by replacing
cot xwith its equivalent,cos x / sin x. This gives us:(cos x / sin x) * sin x * cos x -
Simplify by canceling terms: Notice that
sin xappears in both the numerator and the denominator. We can cancel these terms, provided thatsin x ≠ 0(because division by zero is undefined). This leaves us with:cos x * cos x -
Final simplification: This simplifies to:
cos²x
Therefore, the simplified form of cot x sin x cos x is cos²x, provided that sin x ≠ 0. This condition is important because it ensures the initial expression is defined.
Graphical Representation and Analysis
Visualizing the functions can further solidify our understanding. Let's compare the graphs of y = cot x sin x cos x and y = cos²x. While plotting these functions, remember that cot x is undefined when sin x = 0, which occurs at integer multiples of π (i.e., x = 0, π, 2π, etc.). This leads to vertical asymptotes in the graph of cot x sin x cos x.
However, after simplification, we are left with cos²x, which is a continuous function with a range of [0, 1]. The graph of cos²x is a smooth curve oscillating between 0 and 1. The key observation is that, where both functions are defined, they are equal. The simplification eliminates the discontinuities introduced by cot x.
Applications in Calculus and Physics
The simplified form, cos²x, frequently appears in various mathematical and scientific applications:
-
Calculus: It's often encountered during integration and differentiation problems. For instance, finding the integral of
cos²xinvolves using trigonometric identities or techniques like integration by parts. Understanding its relationship tocot x sin x cos xmight provide alternative approaches to solving such problems. -
Physics: The cosine squared function plays a role in describing phenomena involving oscillations and waves. For example, in the study of simple harmonic motion, the square of the cosine function might appear in expressions representing the energy or displacement of an oscillating system. Also, in wave optics, intensity of light is often proportional to the square of the cosine of an angle.
-
Probability and Statistics: Cosine squared terms can arise in probability distributions related to circular or spherical symmetry.
Exploring Related Trigonometric Identities
The simplification of cot x sin x cos x highlights the importance of understanding and applying fundamental trigonometric identities. Here are some related identities that build upon the concepts discussed:
-
Pythagorean Identity:
sin²x + cos²x = 1. This fundamental identity is frequently used in simplifying trigonometric expressions. -
Reciprocal Identities:
csc x = 1/sin x,sec x = 1/cos x,cot x = 1/tan x = cos x/sin x. These identities define the reciprocal trigonometric functions. -
Quotient Identities:
tan x = sin x/cos x,cot x = cos x/sin x. These relate the tangent and cotangent functions to sine and cosine.
Mastering these identities allows for flexible manipulation and simplification of trigonometric expressions.
Frequently Asked Questions (FAQ)
Q1: What happens if sin x = 0 in the original expression?
A1: If sin x = 0, then cot x is undefined, making the entire expression cot x sin x cos x undefined. The simplification to cos²x is only valid when sin x ≠ 0.
Q2: Can this expression be simplified differently?
A2: While the approach outlined above is the most straightforward, alternative methods might exist, depending on the context and desired outcome. However, the final simplified form will always be equivalent to cos²x (when defined).
Q3: What are some practical applications of this simplification?
A3: The simplification simplifies calculations in various fields, especially in physics and engineering where trigonometric functions are commonly used to model oscillatory motion or wave propagation.
Q4: How can I improve my skills in simplifying trigonometric expressions?
A4: Consistent practice is key. Work through various problems, starting with simpler expressions and gradually increasing complexity. Familiarize yourself with fundamental trigonometric identities and their applications. Utilize online resources and textbooks to enhance your understanding.
Conclusion
Simplifying the trigonometric expression cot x sin x cos x to cos²x demonstrates the power of utilizing fundamental trigonometric identities and algebraic manipulation. This seemingly simple exercise underscores the importance of a strong grasp of trigonometric concepts for success in advanced mathematics, physics, and engineering. By understanding the steps involved, the underlying principles, and the related identities, you can confidently tackle more complex trigonometric problems and gain a deeper appreciation for the elegance and power of trigonometry. Remember that consistent practice and a solid understanding of the foundational principles are key to mastering this crucial area of mathematics.
Latest Posts
Latest Posts
-
How To Complete A Function Table
Sep 21, 2025
-
What Are The Coordinates Of Point B In The Diagram
Sep 21, 2025
-
Determining The Enthalpy Of A Chemical Reaction Lab Answers
Sep 21, 2025
-
Volume Of A Cone In Terms Of Pi
Sep 21, 2025
-
Find Area Of A Parallelogram With Vertices
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Cot X Sin X Cos X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.