Cos X - 1 / X
faraar
Sep 07, 2025 · 6 min read
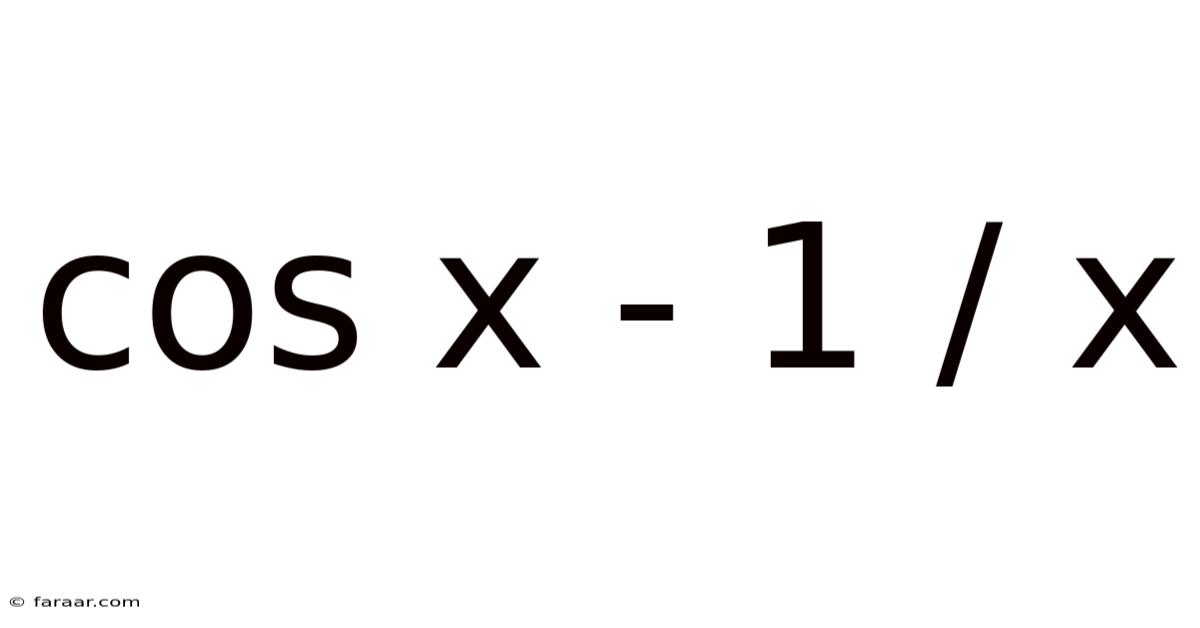
Table of Contents
Exploring the Function: (cos x - 1) / x
The function (cos x - 1) / x presents a fascinating case study in mathematical analysis, blending concepts from trigonometry, limits, and calculus. This article delves deep into understanding this function, exploring its behavior, properties, and applications. We’ll unpack its seemingly simple form to reveal its rich mathematical structure. Understanding this function offers valuable insights into the interplay between trigonometric and algebraic functions, crucial for advanced mathematical studies.
Introduction: A First Glance
At first sight, the function f(x) = (cos x - 1) / x might appear straightforward. However, a closer look reveals complexities. The numerator, (cos x - 1), oscillates between -2 and 0, while the denominator, x, ranges across all real numbers. This immediately highlights a crucial point: the function is undefined at x = 0. This singularity at the origin forms the heart of many of its interesting properties. We’ll explore the function's behavior around this singularity using the powerful tools of limits and series expansions. Our exploration will cover its limit as x approaches 0, its derivatives, its graphical representation, and potential applications within various mathematical contexts.
Understanding the Limit as x Approaches 0
The behavior of f(x) = (cos x - 1) / x near x = 0 is fundamental to understanding the function. We can't simply substitute x = 0, as it leads to an indeterminate form (0/0). Therefore, we employ L'Hôpital's Rule, a powerful tool for evaluating limits of indeterminate forms.
L'Hôpital's Rule states that if the limit of f(x)/g(x) as x approaches a is of the indeterminate form 0/0 or ∞/∞, and if the limit of f'(x)/g'(x) exists, then:
lim (x→a) [f(x)/g(x)] = lim (x→a) [f'(x)/g'(x)]
Applying L'Hôpital's Rule to our function:
f(x) = cos x - 1 g(x) = x
f'(x) = -sin x g'(x) = 1
Therefore,
lim (x→0) [(cos x - 1) / x] = lim (x→0) [-sin x / 1] = -sin(0) = 0
This tells us that as x approaches 0, the function (cos x - 1) / x approaches 0. This seemingly simple result has significant implications for understanding the function's overall behavior.
Taylor Series Expansion: A Deeper Dive
The Taylor series expansion provides another powerful method for analyzing the function around x = 0. The Taylor series expansion for cos x is:
cos x = 1 - x²/2! + x⁴/4! - x⁶/6! + ...
Substituting this into our function:
(cos x - 1) / x = (1 - x²/2! + x⁴/4! - x⁶/6! + ... - 1) / x
= (-x²/2! + x⁴/4! - x⁶/6! + ...) / x
= -x/2! + x³/4! - x⁵/6! + ...
This expansion clearly shows that as x approaches 0, all terms approach 0, confirming our earlier result using L'Hôpital's Rule. The Taylor series also provides a way to approximate the function's value near x = 0 to any desired degree of accuracy.
Graphical Representation and Key Features
Plotting the function reveals its key features. The graph shows the function approaching 0 as x approaches 0. The function is continuous everywhere except at x = 0, where it is undefined. The graph exhibits oscillatory behavior, reflecting the oscillatory nature of the cosine function. The oscillations gradually decrease in amplitude as |x| increases. The graph is symmetric about the y-axis, indicating an even function. This symmetry arises directly from the even nature of the cosine function and the fact that we divide by x, which introduces an odd function component.
Derivatives and Analysis
Analyzing the derivatives of the function provides further insight into its behavior. The first derivative can be found using the quotient rule:
f'(x) = [x(-sin x) - (cos x - 1)] / x²
The second derivative involves more complex calculations but can also be derived using the quotient rule or product rule after simplifying the first derivative. Analyzing the derivatives helps in determining the function's monotonicity, concavity, and the presence of any inflection points. The first derivative will help determine where the function is increasing or decreasing, while the second derivative will reveal its concavity.
Applications and Further Exploration
While (cos x - 1) / x might not have immediately obvious applications like some other mathematical functions, its properties make it relevant in various mathematical contexts. Its Taylor series expansion is used in approximations within numerical analysis. Its behavior near x = 0 is crucial in understanding the behavior of other more complex functions that may incorporate it as a component. Furthermore, this function serves as an excellent example in demonstrating the application of L'Hôpital's rule and Taylor series expansions, enhancing understanding of these fundamental concepts in calculus. Further exploration could involve investigating its integral and its applications within the context of Fourier analysis and other advanced mathematical fields.
Frequently Asked Questions (FAQ)
-
Q: Is the function (cos x - 1) / x continuous?
- A: No, it's discontinuous at x = 0 because it's undefined at that point. However, it has a removable discontinuity; if we define f(0) = 0, the function becomes continuous.
-
Q: What is the significance of the limit as x approaches 0?
- A: The limit being 0 is crucial. It indicates how the function behaves near its singularity, and this behavior influences its overall properties and potential applications.
-
Q: How can I approximate the function's value for small x?
- A: The Taylor series expansion provides a very effective way to approximate the function's value for small x. The more terms you include in the expansion, the more accurate the approximation.
-
Q: Are there any practical applications of this function?
- A: While not having direct, widely used applications like some other functions (such as sine or cosine in physics), it is valuable as a pedagogical tool for understanding key concepts like L'Hopital's rule, Taylor series expansion, and limit calculations. Its properties also appear as components in more complex functions within theoretical mathematics.
-
Q: Why is the function symmetric about the y-axis?
- A: The cosine function is an even function (cos(-x) = cos(x)), and the denominator x is an odd function. The combination of these results in the overall function exhibiting even symmetry.
Conclusion: A Deeper Appreciation
The seemingly simple function (cos x - 1) / x reveals a surprisingly rich mathematical structure. Through exploring its limit, Taylor series expansion, graphical representation, and derivatives, we've gained a deep understanding of its behavior and properties. While it might not have immediate, widely known applications, its pedagogical value in illustrating core concepts in calculus is undeniable. The study of this function highlights the beauty and interconnectedness of different areas of mathematics, emphasizing the power of techniques like L'Hôpital's Rule and Taylor series expansions in unveiling the secrets hidden within seemingly simple mathematical expressions. This deeper appreciation of the function serves as a testament to the constant exploration and discovery at the heart of mathematical study.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 54 And 27
Sep 08, 2025
-
How To Find R In A Scatter Plot
Sep 08, 2025
-
Finding Amplitude Period And Phase Shift
Sep 08, 2025
-
A Playground Ride Consists Of A Disk Of Mass
Sep 08, 2025
-
Which Is A Set Of Valid Quantum Numbers
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Cos X - 1 / X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.