Consider The Curve Given By Xy 2 X 3y 6
faraar
Sep 10, 2025 · 5 min read
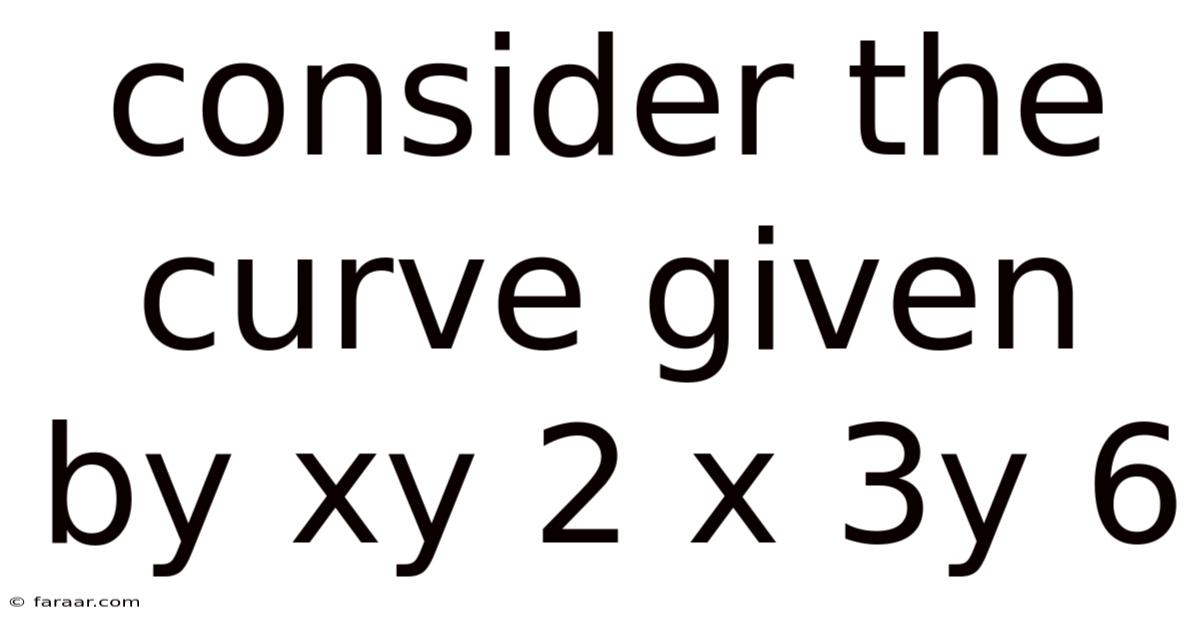
Table of Contents
Exploring the Curve: xy² + x³ - 3y = 6
This article delves into the fascinating properties of the curve defined by the equation xy² + x³ - 3y = 6. We will explore its characteristics, analyze its behavior, and uncover some of its intriguing mathematical secrets. Understanding this curve requires a multi-faceted approach, combining algebraic manipulation, calculus, and graphical analysis. This comprehensive exploration will equip you with a solid understanding of this seemingly simple yet remarkably complex equation.
Introduction: A First Glance at the Curve
The equation xy² + x³ - 3y = 6 represents a implicit curve. Unlike explicit functions where y is explicitly defined in terms of x (e.g., y = x²), this equation implicitly links x and y. This implicit nature makes direct analysis more challenging, but also reveals interesting geometrical properties that wouldn't be apparent in an explicit form. Our journey will involve unraveling these hidden properties through various mathematical tools. We'll explore techniques to find intercepts, asymptotes, and analyze the curve's behavior near critical points. The ultimate goal is to build a comprehensive understanding of this curve's shape and characteristics.
1. Finding Intercepts: Where the Curve Meets the Axes
To find the x-intercepts, we set y = 0 in the equation:
x(0)² + x³ - 3(0) = 6
This simplifies to x³ = 6, which gives us one real x-intercept at x = ∛6 ≈ 1.817.
To find the y-intercepts, we set x = 0:
0(y)² + 0³ - 3y = 6
This simplifies to -3y = 6, giving us a y-intercept at y = -2.
These intercepts provide our first crucial data points for sketching the curve.
2. Implicit Differentiation: Unveiling the Slope
Since we have an implicit equation, we need implicit differentiation to find the slope (dy/dx) at any point on the curve. We differentiate both sides of the equation with respect to x, remembering to use the product rule and chain rule where necessary:
d/dx (xy² + x³ - 3y) = d/dx (6)
This yields:
y² + 2xy(dy/dx) + 3x² - 3(dy/dx) = 0
Now we can solve for dy/dx:
dy/dx (2xy - 3) = -y² - 3x²
dy/dx = (-y² - 3x²) / (2xy - 3)
This equation gives us the slope of the tangent line at any point (x, y) on the curve. The denominator, 2xy - 3, indicates that the slope is undefined when 2xy - 3 = 0, suggesting the presence of vertical tangents.
3. Analyzing Critical Points: Where the Slope is Zero or Undefined
Points where dy/dx = 0: The slope is zero when the numerator is zero and the denominator is non-zero:
-y² - 3x² = 0 => y² = -3x²
This equation has only one real solution: x = 0 and y = 0. However, the point (0,0) is not on the curve because substituting x=0 and y=0 into the original equation gives 0 ≠ 6. Therefore, there are no points where the slope is zero.
Points where dy/dx is undefined: The slope is undefined when the denominator is zero:
2xy - 3 = 0 => y = 3/(2x)
This represents a set of points where the curve might have vertical tangents. To find the exact points, we substitute y = 3/(2x) into the original equation:
x(3/(2x))² + x³ - 3(3/(2x)) = 6
Simplifying this equation leads to a polynomial equation in x, which can be solved to find the x-coordinates of the points with vertical tangents. Solving this equation analytically may be challenging, and numerical methods (like Newton-Raphson) could be employed to approximate the solutions.
4. Asymptotic Behavior: Investigating the Curve's End Behavior
Analyzing the behavior of the curve as x and y approach infinity is crucial for understanding its asymptotic properties. This analysis is often complex for implicit functions. One approach is to consider the equation's behavior for very large values of |x| and |y|. For instance, if we assume |x| and |y| are large, the x³ term might dominate, suggesting that the curve could potentially exhibit cubic-like asymptotic behavior. A more rigorous analysis might involve examining the behavior of the equation along various lines (e.g., y = mx, for different values of m) as x approaches infinity.
5. Sketching the Curve: A Visual Representation
Combining the information gathered from intercepts, slopes, and potential asymptotic behavior, we can attempt to sketch the curve. While an exact graphical representation might require advanced software or numerical methods, we can construct a reasonable sketch using the key points we've identified. We know the curve passes through (∛6, 0) and (0, -2). We also have an idea of where vertical tangents might occur. This qualitative sketch will provide a visual understanding of the curve’s form.
6. Further Analysis: Advanced Techniques
A deeper understanding of this curve might involve more sophisticated mathematical tools:
- Contour Plots: Representing the equation as a contour line of a three-dimensional surface (z = xy² + x³ - 3y - 6) can reveal more about its shape and topology.
- Numerical Methods: Techniques like Newton-Raphson iteration can be used to find approximate solutions for points of interest, such as points with vertical tangents.
- Software Packages: Mathematical software like Mathematica or MATLAB can be used to generate precise plots and analyze the curve's properties more accurately.
7. Frequently Asked Questions (FAQ)
- Q: Is this curve a conic section (ellipse, parabola, hyperbola)? A: No, this curve is not a conic section. Conic sections are defined by second-degree equations, while this equation involves higher-order terms.
- Q: Are there any self-intersections? A: Determining the presence of self-intersections requires a more in-depth analysis, potentially involving solving simultaneous equations derived from the original equation and its derivative.
- Q: Can this curve be expressed in a parametric form? A: While it's possible to attempt to find a parametric representation, it's not guaranteed that a simple and elegant parametric form exists.
8. Conclusion: A Journey of Discovery
The equation xy² + x³ - 3y = 6 presents a rich mathematical landscape. While a complete, analytical description might be challenging, our exploration has revealed key characteristics of the curve: its intercepts, slopes, potential vertical tangents, and asymptotic behavior. Through a combination of algebraic manipulation, calculus, and visual representation, we've gained a substantial understanding of this implicit curve. This journey underscores the power of diverse mathematical techniques when investigating complex geometric relationships. Further exploration using numerical methods or specialized software could refine our understanding and provide even greater insights into the intricacies of this fascinating curve. The ongoing investigation of such implicit curves highlights the dynamic and ever-evolving nature of mathematical discovery.
Latest Posts
Latest Posts
-
Each Pair Of Figures Is Similar Find The Missing Side
Sep 10, 2025
-
The Population Of A Town Increased From 7800 To 8775
Sep 10, 2025
-
What Is The Molar Mass Of Aspirin
Sep 10, 2025
-
How To Say Weeks In Spanish
Sep 10, 2025
-
How Many 1 3 Cups Equal 2 3 Cups
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Consider The Curve Given By Xy 2 X 3y 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.