A Number W Added To 2.3 Is More Than 18
faraar
Sep 02, 2025 · 5 min read
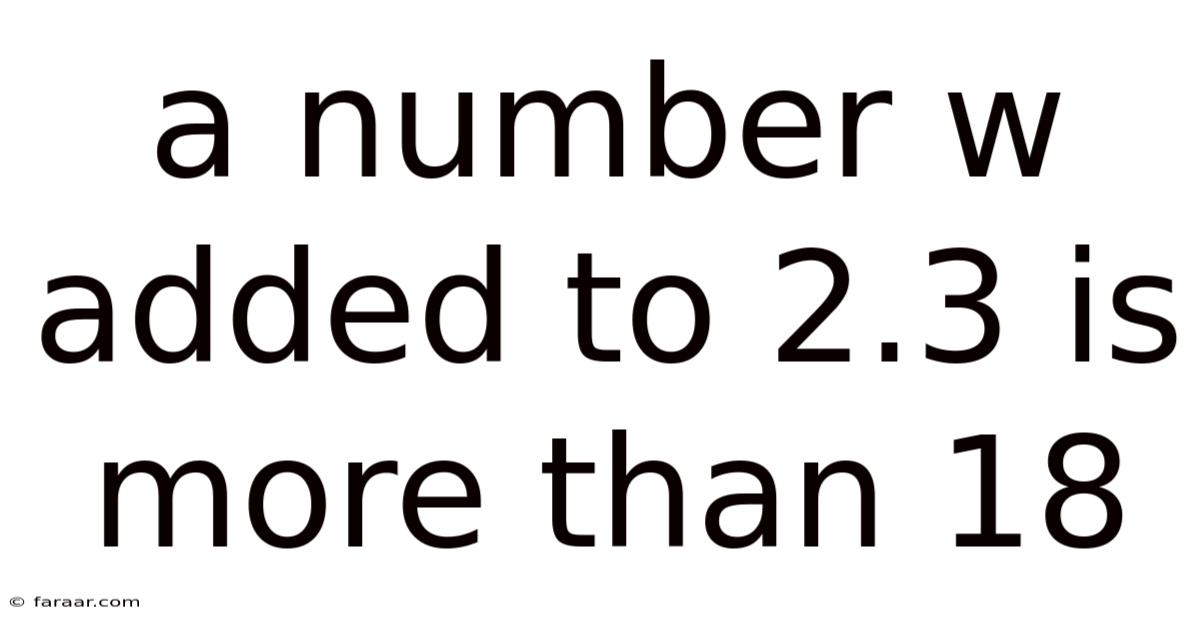
Table of Contents
A Number Added to 2.3 is More Than 18: Unveiling the Mathematical Mystery
This article delves into the seemingly simple yet insightful mathematical problem: "A number w added to 2.3 is more than 18." We'll explore how to solve this inequality, understand its implications, and even delve into more complex scenarios based on this foundational concept. This problem isn't just about finding a single solution; it's about understanding the principles of inequalities and their applications in various mathematical contexts.
Understanding the Problem: Deconstructing the Inequality
The core of the problem lies in translating the written statement into a mathematical inequality. The phrase "a number w added to 2.3" translates directly into the algebraic expression: 2.3 + w. The phrase "is more than 18" signifies that this expression is greater than 18. Therefore, the complete inequality is:
2.3 + w > 18
This inequality tells us that the sum of 2.3 and an unknown number (w) is greater than 18. Our task is to find the possible values of w that satisfy this condition.
Solving the Inequality: A Step-by-Step Approach
Solving inequalities involves manipulating the equation to isolate the variable (w in this case) while maintaining the inequality's direction. Here's the step-by-step solution:
-
Subtract 2.3 from both sides: To isolate w, we need to remove 2.3 from the left side of the inequality. Since we're dealing with an inequality, we must perform the same operation on both sides to maintain the balance.
2.3 + w - 2.3 > 18 - 2.3
-
Simplify: This simplifies the inequality to:
w > 15.7
This means that any number greater than 15.7 will satisfy the original inequality. w can be 15.71, 16, 100, or any larger number. The solution set is an infinite range of numbers.
Visualizing the Solution: The Number Line
A number line provides a visual representation of the solution. You would mark 15.7 on the number line. Then, shade everything to the right of 15.7 because the inequality states that w is greater than 15.7. The open circle at 15.7 indicates that 15.7 itself is not included in the solution set.
Expanding the Concept: Exploring Related Inequalities
Let's explore some related inequalities and how to solve them, building upon the foundational understanding established above.
-
2.3 + w ≥ 18: This inequality includes the equal sign, meaning w can be 15.7 or any number greater than 15.7. The solution on a number line would now include a closed circle at 15.7, indicating its inclusion in the solution set.
-
2.3 + w < 18: This inequality signifies that the sum of 2.3 and w is less than 18. Solving this would involve the same steps as before, but the final result would be w < 15.7. The solution on a number line would be shaded to the left of 15.7, again with an open circle at 15.7.
-
2.3 + w ≤ 18: This is similar to the previous example, but the solution set now includes 15.7 itself, represented by a closed circle at 15.7 on the number line, and the shaded area to its left.
These variations highlight the importance of understanding the symbols (<, >, ≤, ≥) and their implications for the solution sets of inequalities.
Real-World Applications: Inequalities in Action
Inequalities are not just abstract mathematical concepts; they have numerous real-world applications across various fields:
-
Finance: Budgeting involves inequalities. For example, if you have a budget of $100 and want to buy items x and y, the inequality might be: x + y ≤ 100. This ensures you stay within your budget.
-
Engineering: In structural design, inequalities are crucial for ensuring safety margins. For instance, the load capacity (L) of a bridge must be greater than the anticipated weight (W) of vehicles: L > W.
-
Physics: Many physical phenomena are described using inequalities. For example, the speed of an object (v) cannot exceed the speed of light (c): v < c.
-
Computer Science: In algorithms and optimization problems, inequalities are essential for defining constraints and finding optimal solutions.
These examples demonstrate how inequalities play a critical role in problem-solving and decision-making across diverse disciplines.
Further Exploration: Tackling More Complex Inequalities
Let's move beyond the simple inequality we started with and examine a more complex scenario:
3(w + 5) - 7 ≥ 20
To solve this, follow these steps:
-
Distribute: Distribute the 3 across the parentheses: 3w + 15 - 7 ≥ 20
-
Combine like terms: Simplify the left side: 3w + 8 ≥ 20
-
Subtract 8 from both sides: 3w ≥ 12
-
Divide both sides by 3: w ≥ 4
This example shows how solving more complex inequalities involves applying multiple algebraic operations while carefully maintaining the inequality sign.
Frequently Asked Questions (FAQ)
-
Q: What if the inequality was 2.3 + w = 18?
A: This changes the problem from an inequality to an equation. The solution involves subtracting 2.3 from both sides, yielding w = 15.7. This is a single solution, unlike the range of solutions for the inequality.
-
Q: How do I represent the solution graphically for more complex inequalities?
A: The principle remains the same. Once you've isolated the variable, use the number line to represent the solution set. Closed circles indicate inclusion of the boundary value, while open circles indicate exclusion.
-
Q: What are some common mistakes to avoid when solving inequalities?
A: A common mistake is forgetting to reverse the inequality sign when multiplying or dividing both sides by a negative number. Another mistake is incorrectly manipulating the inequality symbols.
Conclusion: Mastering Inequalities – A Foundation for Success
This article has explored the inequality "2.3 + w > 18," offering a detailed solution and contextualizing it within broader mathematical principles. We've seen how solving inequalities involves careful application of algebraic operations, and how the solution set can be visualized using a number line. The numerous real-world applications highlight the practical importance of understanding and mastering inequalities. From budgeting to engineering to computer science, the ability to solve and interpret inequalities is a fundamental skill with far-reaching implications. By understanding the core concepts and practicing with different types of inequalities, you’ll build a strong foundation in mathematics that will serve you well in various academic and professional pursuits. Remember to carefully consider the inequality symbols and the necessary steps to isolate the variable correctly. With consistent practice, mastering inequalities will become second nature, opening up a world of mathematical possibilities.
Latest Posts
Latest Posts
-
What Are 3 Different Types Of Plate Boundaries
Sep 02, 2025
-
Determine The Formula Unit For The Compound Formed
Sep 02, 2025
-
Plants Store Energy In The Form Of
Sep 02, 2025
-
Name An Angle Complementary To Cod
Sep 02, 2025
-
How To Find A Vector Perpendicular To A Plane
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about A Number W Added To 2.3 Is More Than 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.