A Number N Plus 8 Is Greater Than 11
faraar
Sep 14, 2025 · 6 min read
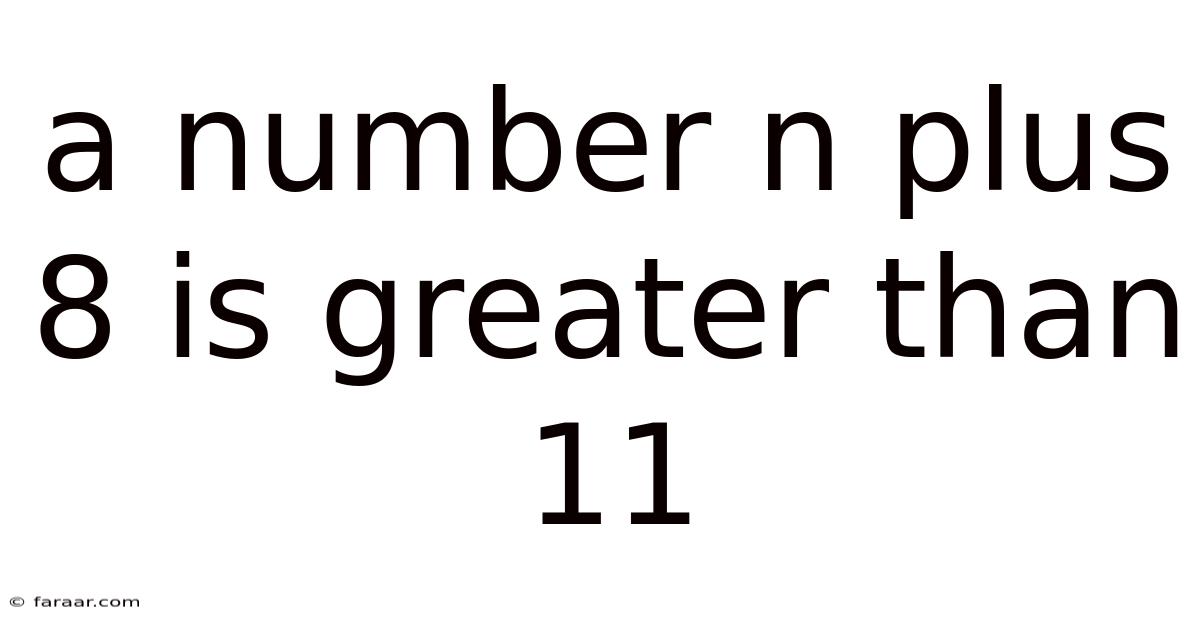
Table of Contents
A Number n Plus 8 is Greater Than 11: Exploring Inequalities and Their Applications
This article delves into the seemingly simple inequality, "a number n plus 8 is greater than 11," exploring its mathematical solution, real-world applications, and the broader concepts of inequalities in mathematics. We'll unravel this seemingly basic problem to reveal its underlying principles and demonstrate how these principles extend to more complex scenarios. Understanding inequalities is crucial for solving problems in various fields, from finance and engineering to computer science and everyday decision-making.
Understanding the Problem: n + 8 > 11
The core of the problem lies in the inequality "n + 8 > 11." This statement translates to: "A number (n) added to 8 results in a value greater than 11." The greater than symbol (>) signifies that the left-hand side (n + 8) must be strictly larger than the right-hand side (11). This isn't an equation where we seek a single solution; instead, we're searching for a range of values for n that satisfy the condition.
Solving the Inequality: Step-by-Step Approach
To solve this inequality, we aim to isolate the variable n on one side of the inequality sign. We can achieve this using the following steps:
-
Subtracting 8 from both sides: To isolate n, we subtract 8 from both sides of the inequality. This maintains the inequality's validity because we perform the same operation on both sides. This gives us:
n + 8 - 8 > 11 - 8
-
Simplifying the equation: This simplifies to:
n > 3
This solution tells us that any number greater than 3 will satisfy the original inequality. n can be 3.1, 4, 100, or even 1,000,000; as long as it's larger than 3, the inequality holds true.
Visualizing the Solution: Number Line Representation
A number line provides a clear visual representation of the solution. We mark the number 3 on the number line. Since n must be greater than 3, we use an open circle (o) at 3 to indicate that 3 itself is not included in the solution set. Then, we shade the region to the right of 3, representing all the numbers greater than 3.
[Diagram of a number line showing an open circle at 3 and shading to the right]
Extending the Concept: More Complex Inequalities
The principle of isolating the variable remains consistent even when dealing with more complex inequalities. Let's consider a few examples:
-
2n + 5 > 15: First, subtract 5 from both sides (2n > 10), then divide both sides by 2 (n > 5). The solution is all numbers greater than 5.
-
3n - 7 < 8: Add 7 to both sides (3n < 15), then divide by 3 (n < 5). The solution is all numbers less than 5.
-
-4n + 10 ≥ 6: Subtract 10 from both sides (-4n ≥ -4), then divide by -4. Important Note: When dividing or multiplying an inequality by a negative number, you must reverse the inequality sign. So, this becomes n ≤ 1. The solution includes 1 and all numbers less than 1.
Real-World Applications of Inequalities
Inequalities are far from abstract mathematical concepts; they find practical application in numerous real-world situations. Here are a few examples:
-
Budgeting: Suppose you have a budget of $100 for groceries. Let x represent the cost of groceries. You need to ensure your grocery spending (x) is less than or equal to $100 (x ≤ 100).
-
Speed Limits: Speed limits on roads are expressed as inequalities. If the speed limit is 65 mph, your speed (s) must be less than or equal to 65 mph (s ≤ 65).
-
Production Targets: A factory might have a daily production target. If the target is 1000 units, the actual production (p) needs to be greater than or equal to 1000 (p ≥ 1000).
-
Temperature Ranges: Weather forecasts often give temperature ranges. A forecast of "highs between 70°F and 80°F" can be represented as 70 ≤ T ≤ 80, where T is the temperature.
-
Profit Margins: Businesses use inequalities to track their profit margins. They want their revenue (R) to be greater than their costs (C) to make a profit (R > C).
Compound Inequalities: Combining Conditions
We can combine multiple inequalities to form compound inequalities. These involve more than one inequality condition. For example:
-
2 < n < 5: This means that n is greater than 2 and less than 5. The solution includes all numbers between 2 and 5 (excluding 2 and 5). This is represented on a number line with open circles at 2 and 5, and shading between them.
-
n ≤ 1 or n ≥ 7: This represents a situation where n is less than or equal to 1 or greater than or equal to 7. On the number line, this would show shading to the left of 1 (including 1) and to the right of 7 (including 7).
Solving Inequalities with Absolute Values
Absolute value inequalities introduce an extra layer of complexity. The absolute value of a number is its distance from zero, always positive. For instance, |3| = 3 and |-3| = 3.
Let's consider the inequality |n - 2| < 5. This means the distance between n and 2 is less than 5. To solve this:
-
Break it into two inequalities: -5 < n - 2 < 5
-
Solve for n: Add 2 to all parts of the inequality: -3 < n < 7
The solution includes all numbers between -3 and 7.
Inequalities and Graphing Linear Equations
Inequalities also play a crucial role in graphing linear equations. Instead of a single line, the solution to a linear inequality is a region of the coordinate plane.
For example, the inequality y > 2x + 1 represents all points above the line y = 2x + 1. The line itself is usually dashed (to indicate points on the line are not included) and the region above the line is shaded.
Frequently Asked Questions (FAQ)
Q: What happens if I multiply or divide an inequality by zero?
A: You cannot multiply or divide an inequality by zero. It renders the inequality meaningless.
Q: Can I add or subtract the same value from both sides of an inequality?
A: Yes, adding or subtracting the same value from both sides of an inequality does not change the inequality's truth.
Q: How do I represent the solution to an inequality on a graph?
A: The solution is usually represented by shading the region on a number line or a coordinate plane that satisfies the inequality. Open circles indicate points not included, and closed circles indicate points included.
Q: What is the difference between > and ≥?
A: ">" means "greater than" (strictly larger), while "≥" means "greater than or equal to."
Conclusion: The Significance of Inequalities
The seemingly simple inequality "n + 8 > 11" serves as a gateway to understanding the broader world of inequalities. From solving basic algebraic problems to tackling more complex scenarios involving absolute values and compound inequalities, the principles discussed here lay a solid foundation. The ability to understand and solve inequalities is not only essential for success in mathematics but also for tackling real-world problems across various disciplines. The ability to translate real-world scenarios into mathematical inequalities is a powerful tool for problem-solving and decision-making. Remember to always carefully consider the implications of the inequality symbols and the operations you perform to ensure you arrive at the correct solution.
Latest Posts
Latest Posts
-
Find The Difference Quotient And Simplify Your Answer
Sep 14, 2025
-
Which Of The Following Relations Is A Function
Sep 14, 2025
-
How To Find Holes And Asymptotes
Sep 14, 2025
-
Does One Gram Equal One Milliliter
Sep 14, 2025
-
What Is The Measurement Of Angle M
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about A Number N Plus 8 Is Greater Than 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.