A Number N Is Less Than 6 Units From 0
faraar
Sep 06, 2025 · 6 min read
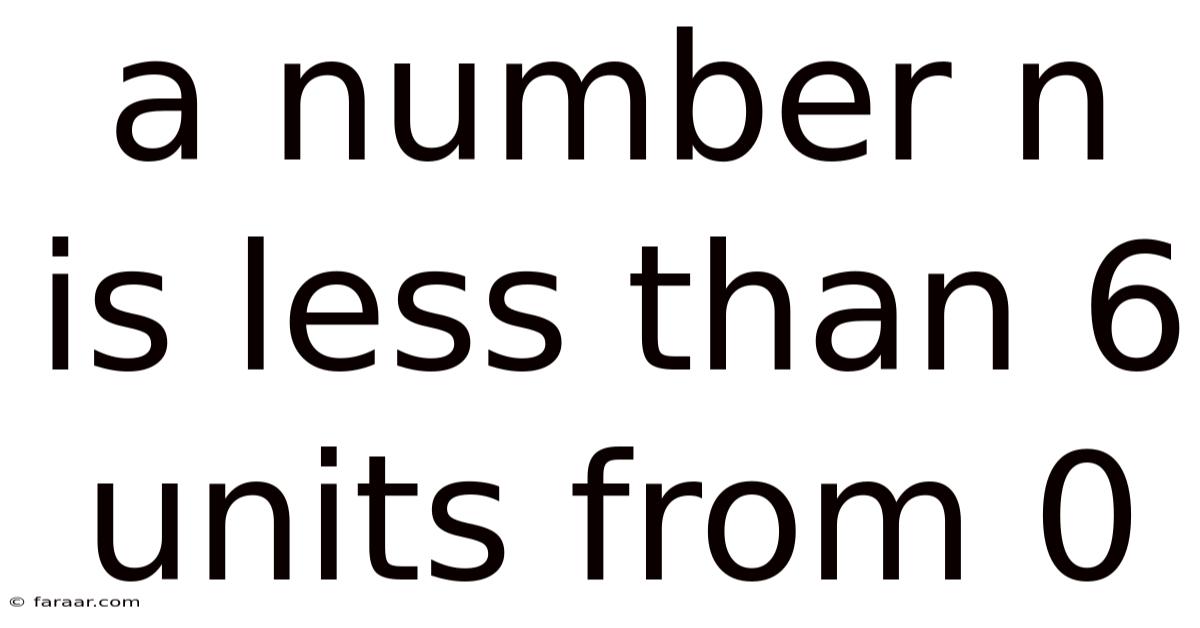
Table of Contents
Exploring the Inequality: |n| < 6
This article delves into the mathematical inequality "|n| < 6," exploring its meaning, implications, and applications. We'll break down the concept step-by-step, making it accessible to a wide audience, from those just beginning their mathematical journey to those seeking a deeper understanding of absolute values and inequalities. Understanding this seemingly simple inequality forms a foundation for more complex mathematical concepts. We will cover its graphical representation, solution methods, and practical applications.
Understanding Absolute Value
Before diving into the inequality, let's solidify our understanding of absolute value. The absolute value of a number, denoted by |n|, represents the distance of that number from zero on the number line. Distance is always positive or zero, so the absolute value of a number is always non-negative.
For example:
- |5| = 5 (The distance from 0 to 5 is 5 units)
- |-5| = 5 (The distance from 0 to -5 is also 5 units)
- |0| = 0 (The distance from 0 to 0 is 0 units)
This concept is crucial for interpreting the inequality "|n| < 6."
Interpreting the Inequality: |n| < 6
The inequality "|n| < 6" states that the absolute value of 'n' is less than 6. In simpler terms, it means that the distance of 'n' from zero is less than 6 units. This implies that 'n' must lie within a specific range on the number line.
To visualize this, imagine a number line centered at zero. The inequality dictates that 'n' must be closer to zero than 6 units in either direction. Therefore, 'n' can be any value between -6 and 6, excluding -6 and 6 themselves.
Solving the Inequality: A Step-by-Step Approach
Solving inequalities involving absolute values requires careful consideration. The inequality |n| < 6 can be broken down into two separate inequalities:
-
n < 6: This inequality represents the positive side of the number line. 'n' can be any value less than 6.
-
n > -6: This inequality represents the negative side of the number line. 'n' must be greater than -6.
Combining these two inequalities, we get the solution: -6 < n < 6. This is called a compound inequality and indicates that 'n' must be greater than -6 and less than 6 simultaneously.
Graphical Representation
Graphically representing the solution set -6 < n < 6 on a number line is straightforward:
- Draw a number line.
- Mark the points -6 and 6.
- Use open circles (or parentheses in interval notation) at -6 and 6 because these values are not included in the solution set.
- Shade the region between -6 and 6 to represent all the values of 'n' that satisfy the inequality.
The graphical representation visually confirms that the solution set consists of all numbers between -6 and 6, excluding -6 and 6 themselves.
Interval Notation
In mathematics, we often use interval notation to express solution sets. The solution to the inequality |n| < 6 in interval notation is (-6, 6). The parentheses indicate that the endpoints -6 and 6 are not included. If the inequality were |n| ≤ 6, the interval notation would be [-6, 6], using square brackets to include the endpoints.
Applications of the Inequality
The inequality |n| < 6, while seemingly simple, has numerous applications in various fields:
-
Engineering and Physics: Tolerance ranges in manufacturing often utilize this type of inequality. For instance, a component might need to be within 6 millimeters of a specified dimension. This ensures that the component functions correctly within acceptable limits.
-
Statistics and Probability: In statistical analysis, we often deal with intervals around a mean or median. The inequality |n| < 6 could represent a range of values within a certain standard deviation from the mean.
-
Computer Science: In algorithms and programming, this inequality might define a search space or a range of acceptable values for a variable. Error bounds and tolerances in calculations frequently use absolute value inequalities.
-
Financial Modeling: Analyzing deviations from a projected value or acceptable levels of risk often involves absolute value inequalities. For example, the acceptable fluctuation in a stock price might be defined using this type of inequality.
-
Real-World Scenarios: Consider a scenario where you are aiming for a target distance of 0 meters, and you must be less than 6 meters away. This inequality would help define the acceptable range of distance from the target.
Extending the Concept: More Complex Inequalities
The principles illustrated with |n| < 6 can be extended to more complex inequalities involving absolute values. For example:
-
|n - a| < b: This inequality represents all values of 'n' that are within 'b' units of 'a'. The solution is a < n < a + b.
-
|n| > 6: This inequality represents all values of 'n' that are more than 6 units away from 0. The solution is n < -6 or n > 6.
Understanding the basic inequality |n| < 6 provides a strong foundation for tackling these more complex scenarios.
Frequently Asked Questions (FAQ)
Q: What if the inequality were |n| ≤ 6?
A: If the inequality were |n| ≤ 6, this means the absolute value of n is less than or equal to 6. The solution would include -6 and 6, resulting in the solution -6 ≤ n ≤ 6, or in interval notation, [-6, 6]. The graphical representation would use closed circles (or square brackets in interval notation) at -6 and 6.
Q: Can I solve this inequality without breaking it into two separate inequalities?
A: While breaking it down is the most straightforward method for beginners, you can also solve it by considering the definition of absolute value. Since |n| < 6, we know that n must be between -6 and 6. This directly gives us the solution -6 < n < 6.
Q: What if 'n' represents a physical quantity, like temperature?
A: The principles remain the same. If 'n' represents temperature in degrees Celsius, and |n| < 6, then the temperature must be between -6°C and 6°C. The units simply add context to the numerical solution.
Q: How does this relate to other mathematical concepts?
A: This inequality is closely related to concepts like intervals, domains, and ranges in functions. It also forms the basis for understanding error bounds and tolerances in various applications.
Conclusion
The seemingly simple inequality |n| < 6 offers a rich opportunity to explore core mathematical concepts, including absolute value, inequalities, and their graphical representations. By understanding its solution and applications, we build a solid foundation for tackling more advanced mathematical problems in various fields. Remember that mastering the fundamentals, like this inequality, is essential for tackling more complex mathematical challenges. The ability to visualize and solve inequalities involving absolute values is a critical skill for success in mathematics and related disciplines. Continue practicing, explore more complex examples, and don't hesitate to ask questions – mathematical understanding is built step-by-step!
Latest Posts
Latest Posts
-
A Solution Is Prepared By Dissolving
Sep 07, 2025
-
Which Of The Following Is The Best
Sep 07, 2025
-
Round To The Highest Place Value
Sep 07, 2025
-
Which Solution Has The Highest Boiling Point At Standard Pressure
Sep 07, 2025
-
How To Get Rid Of A Negative Power
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about A Number N Is Less Than 6 Units From 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.