A Number Is More Than 12 Units From 0
faraar
Sep 13, 2025 · 6 min read
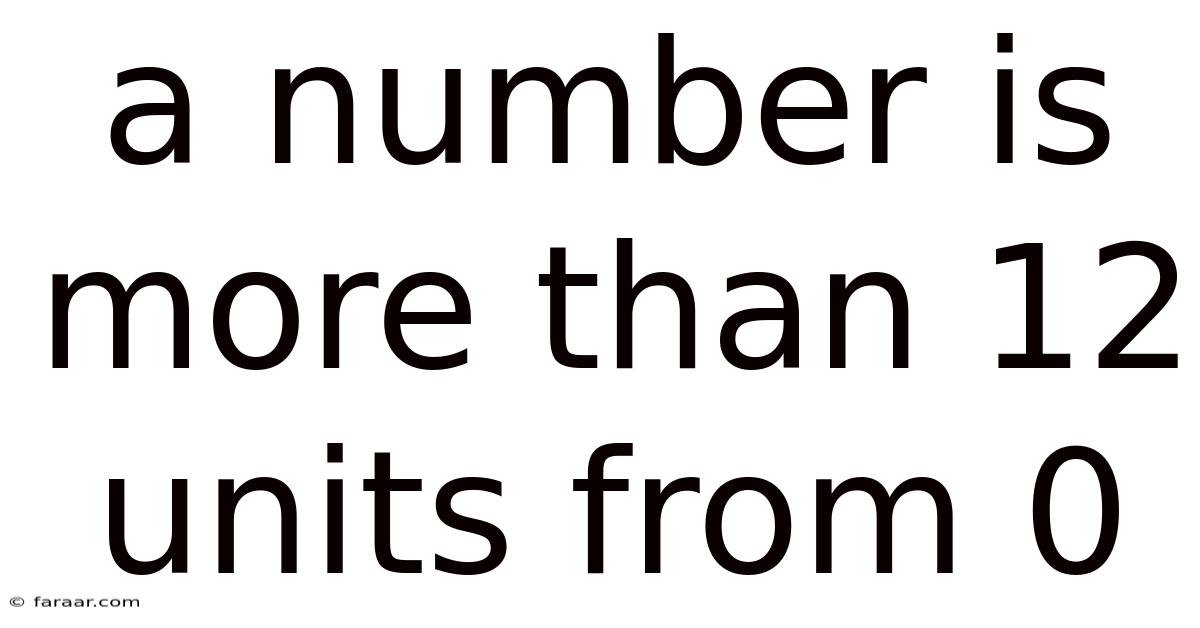
Table of Contents
Exploring Numbers Beyond 12 Units from Zero: A Deep Dive into Absolute Value and Inequalities
This article delves into the mathematical concept of a number being more than 12 units away from zero. We'll explore this concept using the principles of absolute value and inequalities, clarifying the meaning, providing practical examples, and examining the broader implications within mathematics. Understanding this concept is crucial for various mathematical applications, from basic algebra to more advanced calculus and beyond. This exploration will be accessible to a wide audience, regardless of their prior mathematical background.
Understanding Absolute Value
Before we tackle the main topic, let's solidify our understanding of absolute value. The absolute value of a number is its distance from zero on the number line. It's always a non-negative value. We denote the absolute value of a number 'x' as |x|.
For example:
- |5| = 5 (The distance between 5 and 0 is 5 units)
- |-5| = 5 (The distance between -5 and 0 is also 5 units)
- |0| = 0 (The distance between 0 and 0 is 0 units)
The absolute value function essentially "strips away" the negative sign, if present, leaving only the magnitude of the number. This is crucial for representing distances, which are always positive or zero.
Representing "More Than 12 Units from Zero" Mathematically
The statement "a number is more than 12 units from 0" translates directly into an inequality involving absolute value. Let's represent the number as 'x'. The inequality is expressed as:
|x| > 12
This inequality states that the distance of 'x' from zero is greater than 12 units. This means 'x' can be either significantly positive or significantly negative.
Solving the Inequality |x| > 12
To solve this inequality, we need to consider two separate cases:
Case 1: x ≥ 0
If x is non-negative, then |x| = x. The inequality becomes:
x > 12
This means any number greater than 12 satisfies the condition.
Case 2: x < 0
If x is negative, then |x| = -x. The inequality becomes:
-x > 12
To solve for x, we multiply both sides by -1, remembering to reverse the inequality sign:
x < -12
This means any number less than -12 satisfies the condition.
Therefore, the complete solution to the inequality |x| > 12 is:
x > 12 or x < -12
This solution encompasses all numbers greater than 12 and all numbers less than -12. These numbers are more than 12 units away from zero on the number line.
Visual Representation on the Number Line
A number line provides a clear visual representation of the solution. We mark -12 and 12 on the number line. The solution to the inequality |x| > 12 includes all values to the right of 12 and all values to the left of -12. The points -12 and 12 themselves are not included because the inequality is strictly greater than (>) and not greater than or equal to (≥).
<-----------------|----------------->
-12 0 12
The shaded regions represent the solution set.
Real-World Applications
The concept of a number being more than a certain distance from zero has many practical applications:
-
Temperature: If the acceptable temperature range for a certain process is between -10°C and 10°C, then any temperature outside the range |T| > 10°C would be considered unacceptable.
-
Measurement Tolerance: In manufacturing, there might be a tolerance range for the length of a component. If the ideal length is 100 mm with a tolerance of ±5 mm, any length where |L - 100| > 5 mm would be considered defective.
-
Finance: A financial model might predict a certain value (e.g., stock price) to be within a specified range from a predicted value. Values outside this range, represented by an absolute value inequality, might trigger alerts or further investigation.
-
Physics: In physics, absolute value is often used to represent magnitudes of physical quantities like velocity or acceleration, regardless of direction. For instance, if a speed must be more than 25 mph, we could write |v| > 25, where v represents the velocity.
-
Statistics: In hypothesis testing, the absolute difference between observed and expected values is compared to a critical value. If the absolute difference is larger than the critical value, the null hypothesis might be rejected.
Exploring Variations: |x| ≥ 12
Let's consider a slightly different inequality: |x| ≥ 12. This inequality includes the endpoints -12 and 12. The solution to this inequality would be:
x ≥ 12 or x ≤ -12
The number line representation would show shaded regions similar to the previous example but including the points -12 and 12.
<-----------------|----------------->
-12 0 12
The closed circles at -12 and 12 indicate that these values are now part of the solution set.
Solving More Complex Absolute Value Inequalities
The principles discussed above can be extended to solve more complex absolute value inequalities. For example:
|x - 5| > 3
This inequality represents numbers whose distance from 5 is greater than 3. We solve this using similar case analysis:
Case 1: x - 5 ≥ 0 (This means x ≥ 5)
x - 5 > 3 x > 8
Case 2: x - 5 < 0 (This means x < 5)
-(x - 5) > 3 -x + 5 > 3 -x > -2 x < 2
Therefore, the solution to |x - 5| > 3 is x > 8 or x < 2.
Frequently Asked Questions (FAQ)
Q: What happens if the inequality is |x| < 12?
A: The inequality |x| < 12 represents numbers whose distance from zero is less than 12. This means -12 < x < 12. The solution is all numbers between -12 and 12 (excluding -12 and 12 themselves).
Q: Can I solve absolute value inequalities graphically?
A: Yes, you can visualize the solutions graphically by plotting the function y = |x| and the horizontal line y = 12 (or the relevant value). The solution to |x| > 12 will be the x-values where the graph of y = |x| is above the line y = 12.
Q: What if the inequality involves a different number than 12?
A: The principles remain the same. Replace 12 with the given number and follow the same steps to solve the inequality. For example, |x| > 5 would have solutions x > 5 or x < -5.
Q: Are there any limitations to using absolute value to represent distance?
A: In higher dimensions (more than one dimension), the concept of distance is more complex. While absolute value works well for one-dimensional distance, we use the Pythagorean theorem or distance formulas for calculating distances in two or more dimensions.
Conclusion
Understanding the concept of a number being more than 12 units from zero is fundamental to grasping the power of absolute value and inequalities. By applying the principles of case analysis, we can solve these inequalities and interpret the results in various contexts. This concept's relevance extends beyond theoretical mathematics, providing a powerful tool for solving real-world problems in diverse fields like engineering, finance, and science. Mastering these concepts opens doors to more advanced mathematical explorations and problem-solving capabilities. The ability to translate a word problem into a precise mathematical inequality and then effectively solve it is a critical skill in any quantitative field. Remember, practice is key to mastering these concepts and their applications. Through continued practice and exploration, you'll develop a solid foundation for tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
What Is Half Of 1 3 4 Inches
Sep 13, 2025
-
Which Of The Following Functions Are Continuous On The Interval
Sep 13, 2025
-
Dividing A Positive Number By A Negative Number
Sep 13, 2025
-
How To Calculate The Concentration Of Protein From Absorbance
Sep 13, 2025
-
How Many Bags Concrete Per Yard
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about A Number Is More Than 12 Units From 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.