A Number Is At Most 45
faraar
Sep 11, 2025 · 6 min read
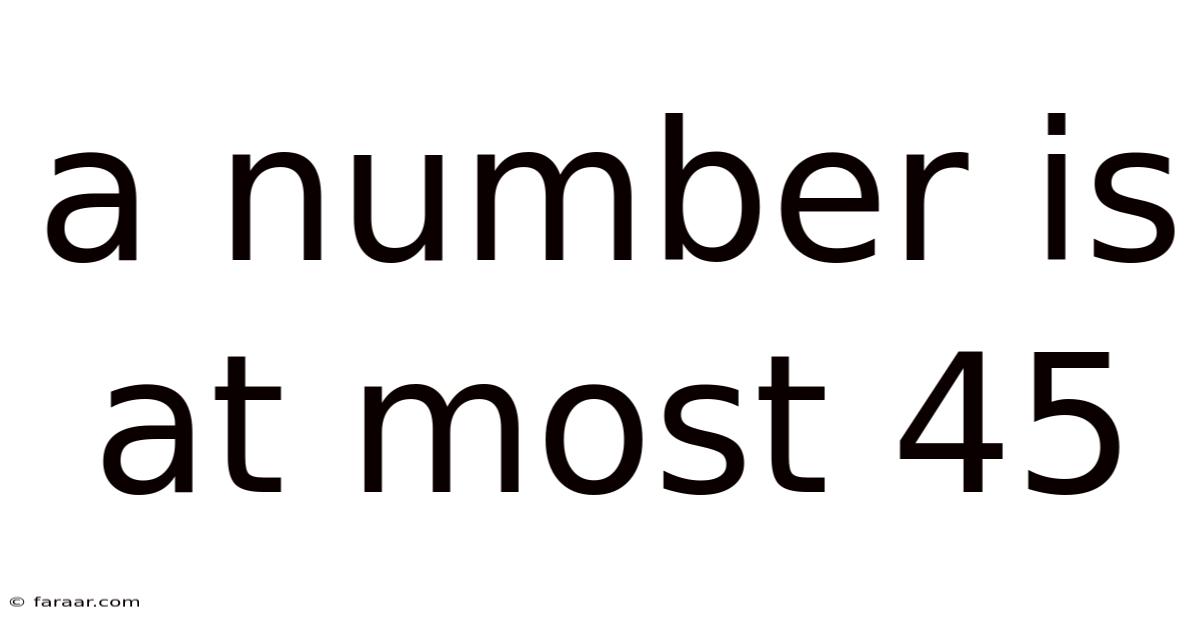
Table of Contents
A Number is at Most 45: Understanding Inequalities and Their Applications
This article delves into the mathematical concept of "a number is at most 45," exploring its meaning within the context of inequalities, demonstrating how to represent it algebraically and graphically, and exploring its applications in various real-world scenarios. We will also examine related concepts and answer frequently asked questions to provide a comprehensive understanding of this seemingly simple yet fundamentally important mathematical idea.
Introduction: Understanding Inequalities
In mathematics, an inequality is a statement that compares two values, showing if one is less than, greater than, less than or equal to, or greater than or equal to another value. Unlike equations, which use an equals sign (=), inequalities use symbols such as < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to). The statement "a number is at most 45" directly translates to an inequality.
Representing "A Number is at Most 45" Algebraically
The phrase "at most" implies that the number can be 45 or any value less than 45. This is represented algebraically using the "less than or equal to" symbol (≤). Let's use the variable 'x' to represent the number. The inequality is then written as:
x ≤ 45
This concisely states that the value of x is less than or equal to 45. Any number satisfying this condition (e.g., 45, 0, -10, 44.99) makes the inequality true.
Graphical Representation of x ≤ 45
Inequalities can be visually represented on a number line. To graph x ≤ 45:
-
Draw a number line: Draw a horizontal line with numbers marked, including 45.
-
Locate 45: Find the point representing 45 on the number line.
-
Indicate the inequality: Since the inequality includes "or equal to," we use a closed circle (or a filled-in dot) at 45 to show that 45 is included in the solution set.
-
Shade the region: Shade the portion of the number line to the left of 45. This shaded region represents all the numbers that are less than or equal to 45.
This visual representation clearly shows the range of values that satisfy the inequality x ≤ 45.
Solving Inequalities Involving "At Most"
Understanding how to solve inequalities is crucial. Let's look at an example:
"The sum of a number and 10 is at most 45. Find the possible values of the number."
-
Translate to an inequality: Let 'y' represent the number. The problem translates to: y + 10 ≤ 45
-
Solve the inequality: To isolate 'y', subtract 10 from both sides: y ≤ 45 - 10 => y ≤ 35
Therefore, the number (y) can be any value less than or equal to 35.
Real-World Applications of "At Most" Inequalities
The concept of "at most" appears frequently in real-world scenarios:
-
Weight restrictions: A truck carrying goods might have a weight restriction of "at most 20 tons." This translates to weight ≤ 20 tons.
-
Speed limits: Speed limits on roads are often expressed as "at most 65 mph." This means speed ≤ 65 mph.
-
Budgeting: If you have a budget of "$100 at most" for groceries, then grocery cost ≤ $100.
-
Inventory Management: A warehouse might have a capacity of “at most 1000 units” of a particular product. This translates to number of units ≤ 1000.
-
Time constraints: A project might have a deadline stipulating that it must be completed "in at most 3 weeks." This would translate to project completion time ≤ 3 weeks.
-
Temperature limits: Scientific experiments may require the temperature of a solution to be maintained "at most 25°C" (temperature ≤ 25°C) to ensure accurate results.
These examples illustrate how the seemingly simple concept of "at most" has practical relevance across many fields.
Distinguishing "At Most" from "At Least"
It's vital to distinguish between "at most" (≤) and "at least" (≥). "At least" indicates a minimum value; the number can be that value or greater. For instance, "a number is at least 10" translates to x ≥ 10. Confusing these two concepts can lead to incorrect solutions in problem-solving.
Compound Inequalities Involving "At Most"
Sometimes, you might encounter compound inequalities, where a number is constrained by multiple conditions. For example: "A number is at most 45 and at least 15." This would be expressed as:
15 ≤ x ≤ 45
This indicates that x must fall within the range of 15 to 45, inclusive.
Solving More Complex Inequalities
Let's consider a slightly more complex scenario:
"Twice a number, decreased by 5, is at most 35. Find the number."
-
Translate to an inequality: Let the number be 'z'. The problem is: 2z - 5 ≤ 35
-
Solve the inequality:
- Add 5 to both sides: 2z ≤ 40
- Divide both sides by 2: z ≤ 20
Therefore, the number (z) can be any value less than or equal to 20.
Inequalities and Absolute Value
Inequalities can also involve absolute values. For example, "|x| ≤ 45" means that the distance of x from 0 is at most 45. This is equivalent to:
-45 ≤ x ≤ 45
Applications in Advanced Mathematics
The concept of inequalities extends beyond basic algebra. It plays a vital role in:
-
Calculus: Inequalities are used to define limits and derivatives.
-
Linear Programming: Optimization problems frequently involve inequalities to define constraints.
-
Statistics: Inequalities are used in probability and hypothesis testing.
-
Game Theory: Inequalities are used to model strategic interactions and optimal strategies.
These advanced applications highlight the broad and significant impact of inequalities across mathematical disciplines.
Frequently Asked Questions (FAQ)
Q1: What is the difference between x < 45 and x ≤ 45?
A1: x < 45 means x is strictly less than 45; 45 is not included. x ≤ 45 means x is less than or equal to 45; 45 is included.
Q2: Can I multiply or divide both sides of an inequality by a negative number?
A2: Yes, but you must reverse the inequality sign. For example, if -2x ≤ 10, then dividing by -2 gives x ≥ -5.
Q3: How do I solve inequalities with multiple variables?
A3: Solving inequalities with multiple variables often involves manipulating the inequality to isolate one variable in terms of the others. Techniques like substitution or elimination can be used, similar to solving systems of equations.
Q4: How do I represent an inequality graphically in more than one dimension?
A4: For inequalities involving two variables (e.g., x + y ≤ 10), you represent the solution set as a region on a Cartesian coordinate plane. The inequality defines a boundary line, and shading indicates the region satisfying the inequality.
Conclusion: The Significance of "At Most"
The seemingly simple concept of "a number is at most 45" represents a fundamental building block in mathematics. Understanding inequalities, their algebraic and graphical representations, and their diverse applications is essential not only for success in mathematics but also for navigating and understanding many aspects of the real world. From setting budgets to interpreting scientific data, the ability to translate and work with inequalities is a valuable skill applicable across various disciplines. By grasping the core concepts presented here, you equip yourself with a powerful tool for problem-solving and critical thinking in numerous contexts.
Latest Posts
Latest Posts
-
Find The Polynomial With The Given Roots
Sep 12, 2025
-
How Much Is 2 3 In Cups
Sep 12, 2025
-
What Shape Has 4 Congruent Sides
Sep 12, 2025
-
How To Start A Collage Essay
Sep 12, 2025
-
As Mass Increases What Happens To The Volume
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about A Number Is At Most 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.