A Bh 2 Solve For B
faraar
Sep 15, 2025 · 6 min read
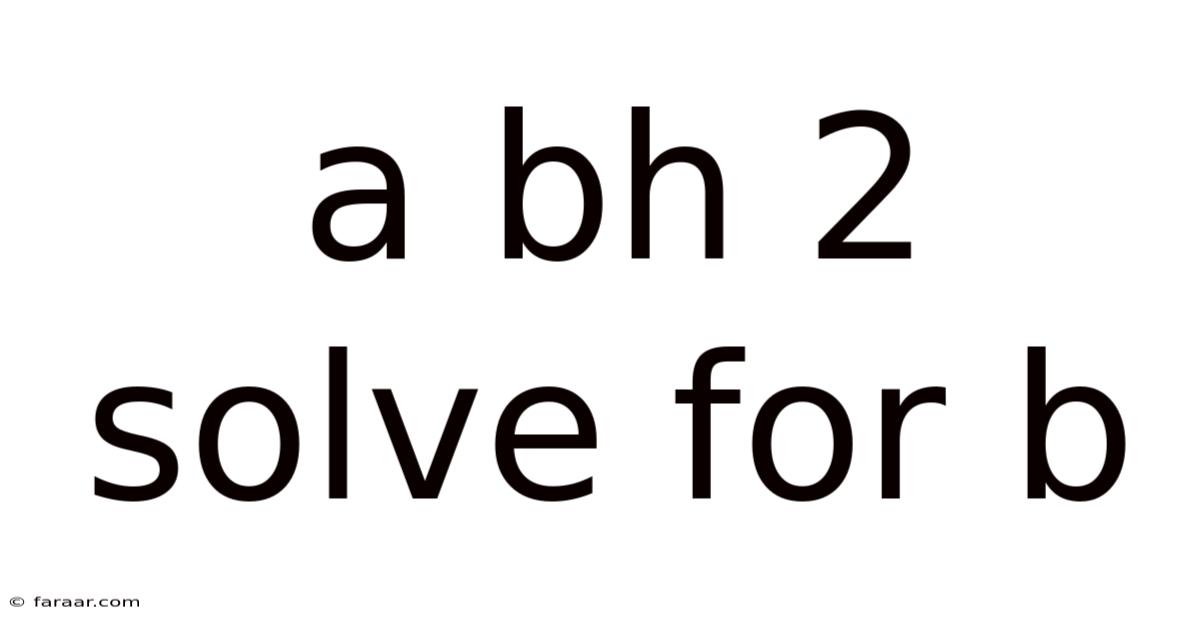
Table of Contents
Solving for b: A Comprehensive Guide to Algebraic Equations
This article provides a comprehensive guide on how to solve for the variable 'b' in various algebraic equations. We'll cover a range of scenarios, from simple one-step equations to more complex multi-step equations involving fractions, exponents, and even systems of equations. Understanding how to isolate 'b' is a fundamental skill in algebra, essential for tackling more advanced mathematical concepts. Whether you're a student brushing up on your algebra skills or simply curious about solving equations, this guide will equip you with the knowledge and confidence to tackle any equation containing 'b'.
Understanding the Basics: What Does "Solving for b" Mean?
"Solving for b" means manipulating an equation to isolate the variable 'b' on one side of the equals sign, expressing it in terms of other variables and constants. This involves applying inverse operations to undo any operations performed on 'b'. The goal is to find the value or expression that 'b' represents given the values of other variables within the equation. Let's explore this with some examples.
Solving Simple Equations for b
Let's start with the simplest cases, involving only one step to isolate 'b'.
Example 1: b + 5 = 10
To solve for 'b', we need to remove the 5 from the left side. Since 5 is added to 'b', we perform the inverse operation – subtraction. Subtract 5 from both sides of the equation:
b + 5 - 5 = 10 - 5
This simplifies to:
b = 5
Example 2: b - 7 = 3
Here, 7 is subtracted from 'b'. The inverse operation is addition. Add 7 to both sides:
b - 7 + 7 = 3 + 7
This simplifies to:
b = 10
Example 3: 5b = 25
In this case, 'b' is multiplied by 5. The inverse operation is division. Divide both sides by 5:
5b / 5 = 25 / 5
This simplifies to:
b = 5
Example 4: b/3 = 6
Here, 'b' is divided by 3. The inverse operation is multiplication. Multiply both sides by 3:
(b/3) * 3 = 6 * 3
This simplifies to:
b = 18
Solving Multi-Step Equations for b
Moving on to more complex equations that require multiple steps to isolate 'b'. These typically involve a combination of addition, subtraction, multiplication, and division. Remember the order of operations (PEMDAS/BODMAS) when dealing with parentheses and exponents. Always work to simplify the equation before attempting to isolate 'b'.
Example 5: 2b + 7 = 15
- Subtract 7 from both sides: 2b + 7 - 7 = 15 - 7 => 2b = 8
- Divide both sides by 2: 2b / 2 = 8 / 2 => b = 4
Example 6: 3b - 5 = 16
- Add 5 to both sides: 3b - 5 + 5 = 16 + 5 => 3b = 21
- Divide both sides by 3: 3b / 3 = 21 / 3 => b = 7
Example 7: (b/4) + 2 = 7
- Subtract 2 from both sides: (b/4) + 2 - 2 = 7 - 2 => b/4 = 5
- Multiply both sides by 4: (b/4) * 4 = 5 * 4 => b = 20
Example 8: 5(b - 2) = 15
- Divide both sides by 5: 5(b - 2) / 5 = 15 / 5 => b - 2 = 3
- Add 2 to both sides: b - 2 + 2 = 3 + 2 => b = 5
Solving Equations with Fractions for b
Equations involving fractions require an extra step to eliminate the denominators. The most common technique is to multiply both sides of the equation by the least common denominator (LCD).
Example 9: b/2 + b/3 = 5
- Find the LCD: The LCD of 2 and 3 is 6.
- Multiply both sides by the LCD: 6 * (b/2 + b/3) = 6 * 5 => 3b + 2b = 30
- Combine like terms: 5b = 30
- Divide both sides by 5: 5b / 5 = 30 / 5 => b = 6
Example 10: (2b/5) - 1 = 3
- Add 1 to both sides: (2b/5) - 1 + 1 = 3 + 1 => 2b/5 = 4
- Multiply both sides by 5: (2b/5) * 5 = 4 * 5 => 2b = 20
- Divide both sides by 2: 2b / 2 = 20 / 2 => b = 10
Solving Equations with Exponents for b
Equations with exponents require applying the rules of exponents to isolate 'b'. This often involves taking roots or using logarithmic functions.
Example 11: b² = 25
- Take the square root of both sides: √b² = ±√25 => b = ±5 (Remember that both positive and negative solutions are possible when taking an even root).
Example 12: 2<sup>b</sup> = 8
- Rewrite 8 as a power of 2: 2<sup>b</sup> = 2<sup>3</sup>
- Since the bases are equal, the exponents must be equal: b = 3
Solving Systems of Equations for b
Sometimes, 'b' is part of a system of equations. This requires using techniques like substitution or elimination to solve for 'b'.
Example 13: 2a + b = 7 a - b = 2
- Solve one equation for one variable: Let's solve the second equation for 'a': a = b + 2
- Substitute this expression for 'a' into the first equation: 2(b + 2) + b = 7
- Simplify and solve for 'b': 2b + 4 + b = 7 => 3b = 3 => b = 1
- Substitute the value of 'b' back into either original equation to solve for 'a'.
Common Mistakes to Avoid
- Incorrect order of operations: Remember PEMDAS/BODMAS.
- Errors in signs: Be careful with positive and negative numbers.
- Forgetting to apply operations to both sides: Always maintain the balance of the equation.
- Incorrectly simplifying expressions: Double-check your algebra.
Frequently Asked Questions (FAQ)
Q: What if the equation has no solution for b?
A: Some equations have no solution. This means there's no value of 'b' that will satisfy the equation. For example, an equation like 2b + 2 = 2b + 5 has no solution, as the '2b' terms cancel out, leaving a false statement (2 = 5).
Q: What if the equation has multiple solutions for b?
A: Some equations, particularly those with higher-order terms (like quadratic equations), can have multiple solutions for 'b'. This is common when dealing with even-numbered exponents.
Q: How can I check my answer?
A: Once you've solved for 'b', substitute your solution back into the original equation. If the equation holds true, your answer is correct.
Conclusion
Solving for 'b' is a fundamental algebraic skill that builds a strong foundation for more advanced mathematical concepts. By mastering the techniques outlined in this guide, you'll be well-equipped to tackle a wide range of algebraic problems, building confidence and proficiency in your mathematical abilities. Remember to practice regularly, work through different types of equations, and always double-check your work. With consistent effort and attention to detail, you will become a proficient solver of algebraic equations.
Latest Posts
Latest Posts
-
How Can Density Be Used As A Conversion Factor
Sep 15, 2025
-
How To Factor X 3 125
Sep 15, 2025
-
What Does Without Bound Mean In Math
Sep 15, 2025
-
What Is The Area Of This Circle In Square Centimeters
Sep 15, 2025
-
How Much Is 5 G Of Sugar
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about A Bh 2 Solve For B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.