A 1 2 B1 B2 H Solve For B1
faraar
Sep 08, 2025 · 5 min read
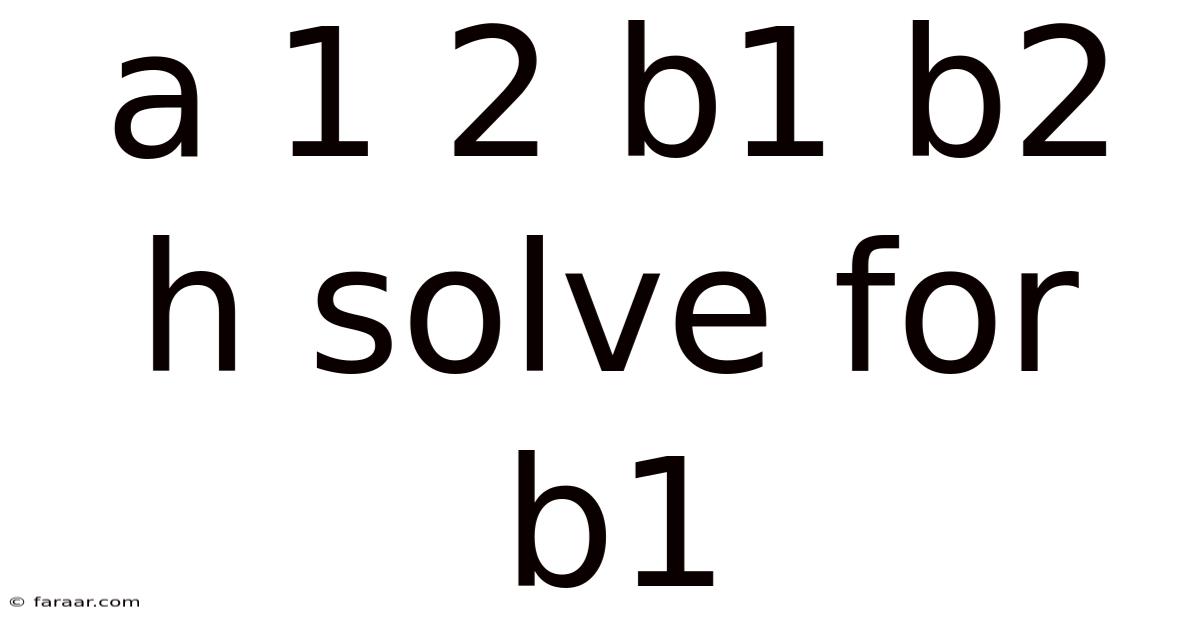
Table of Contents
Solving for b1: A Deep Dive into Algebraic Manipulation
This article provides a comprehensive guide on how to solve for b1 in the equation a = 1/2(b1 + b2)h, a formula commonly used in geometry to calculate the area of a trapezoid. We will explore the algebraic steps involved, provide a step-by-step solution, address potential confusion points, and delve into the underlying mathematical principles. Understanding this seemingly simple equation unlocks a deeper appreciation for algebraic manipulation and its applications in various fields.
Understanding the Trapezoid Area Formula
Before we dive into solving for b1, let's understand the context of the equation: a = 1/2(b1 + b2)h. This formula calculates the area (a) of a trapezoid. Let's break down each component:
- a: Represents the area of the trapezoid. This is the value we often want to find, but in our case, it's given.
- b1: Represents the length of one of the parallel sides of the trapezoid (the bases). This is the variable we are solving for.
- b2: Represents the length of the other parallel side of the trapezoid. This value is usually given.
- h: Represents the height of the trapezoid – the perpendicular distance between the two parallel sides. This value is also usually given.
Step-by-Step Solution for b1
Now, let's tackle the core of the article: solving for b1. Our goal is to isolate b1 on one side of the equation. We'll do this using a series of algebraic manipulations.
1. Eliminate the Fraction:
The equation begins with a fraction (1/2). To simplify, we can multiply both sides of the equation by 2:
2a = (b1 + b2)h
2. Expand the Parentheses:
While not strictly necessary, expanding the parentheses can improve clarity:
2a = b1h + b2h
3. Isolate the Term Containing b1:
Our goal is to get b1 by itself. To do this, we need to move the term 'b2h' to the other side of the equation. We can achieve this by subtracting b2h from both sides:
2a - b2h = b1h
4. Solve for b1:
Finally, to completely isolate b1, we divide both sides of the equation by 'h':
(2a - b2h) / h = b1
Therefore, the solution for b1 is:
b1 = (2a - b2h) / h
Illustrative Example
Let's solidify our understanding with a numerical example. Suppose we have a trapezoid with the following dimensions:
- a (area) = 30 square units
- b2 (base 2) = 8 units
- h (height) = 5 units
We can plug these values into our solved equation:
b1 = (2 * 30 - 8 * 5) / 5
b1 = (60 - 40) / 5
b1 = 20 / 5
b1 = 4 units
Therefore, the length of the other base (b1) is 4 units.
Understanding the Algebraic Principles Involved
The solution process utilizes fundamental algebraic principles:
- The distributive property: Used when expanding the parentheses in step 2. This property states that a(b + c) = ab + ac.
- The addition and subtraction property of equality: Used in step 3. This property states that adding or subtracting the same value from both sides of an equation maintains equality.
- The multiplication and division property of equality: Used in steps 1 and 4. This property states that multiplying or dividing both sides of an equation by the same non-zero value maintains equality.
Addressing Common Mistakes and Confusion
Several common mistakes can arise when solving for b1:
- Incorrect order of operations: Remember to follow the order of operations (PEMDAS/BODMAS) correctly. Parentheses, exponents, multiplication and division (from left to right), addition and subtraction (from left to right).
- Errors in algebraic manipulation: Carefully track your signs and ensure you're performing the correct operations on both sides of the equation. Double-check each step.
- Dividing by zero: Avoid dividing by zero. If 'h' is zero, the trapezoid has no height, and the formula is undefined.
Frequently Asked Questions (FAQ)
Q1: What if I'm given the area and the lengths of both bases, and I need to solve for the height (h)?
A1: Rearrange the original formula to solve for h. Start with the formula 2a = (b1 + b2)h and divide both sides by (b1 + b2):
h = 2a / (b1 + b2)
Q2: Can this formula be used for other shapes?
A2: No, this specific formula is exclusively for trapezoids. Other shapes have different area formulas.
Q3: What happens if b1 and b2 are equal?
A3: If b1 and b2 are equal, the trapezoid becomes a parallelogram, and the formula simplifies to a = b1 * h (or a = b2 * h, since they are equal).
Q4: Why is it important to understand this algebraic manipulation?
A4: Mastering algebraic manipulation is crucial for problem-solving in various fields, including mathematics, physics, engineering, and computer science. It enables us to solve for unknown variables and extract meaningful insights from mathematical models. This specific example demonstrates a practical application of these skills in a geometric context.
Conclusion
Solving for b1 in the trapezoid area formula, a = 1/2(b1 + b2)h, provides a practical illustration of fundamental algebraic principles. By systematically applying algebraic manipulation techniques, we can successfully isolate the desired variable and obtain a solution. Understanding this process enhances problem-solving skills and strengthens our grasp of algebraic concepts. Remember to always double-check your work, follow the order of operations, and be mindful of potential pitfalls like division by zero. With practice, solving for b1 (and other variables in similar equations) becomes a straightforward and rewarding exercise. The ability to manipulate equations efficiently is a valuable asset in numerous academic and professional endeavors.
Latest Posts
Latest Posts
-
How To Solve Slope Word Problems
Sep 09, 2025
-
A Parallelogram With 4 Congruent Sides
Sep 09, 2025
-
Which Ordered Pair Comes From The Table Apex
Sep 09, 2025
-
What Is 35 In A Fraction
Sep 09, 2025
-
Writing The Half Reactions Of A Single Displacement Reaction
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about A 1 2 B1 B2 H Solve For B1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.