9 Less Than Six Times A Number
faraar
Sep 12, 2025 · 6 min read
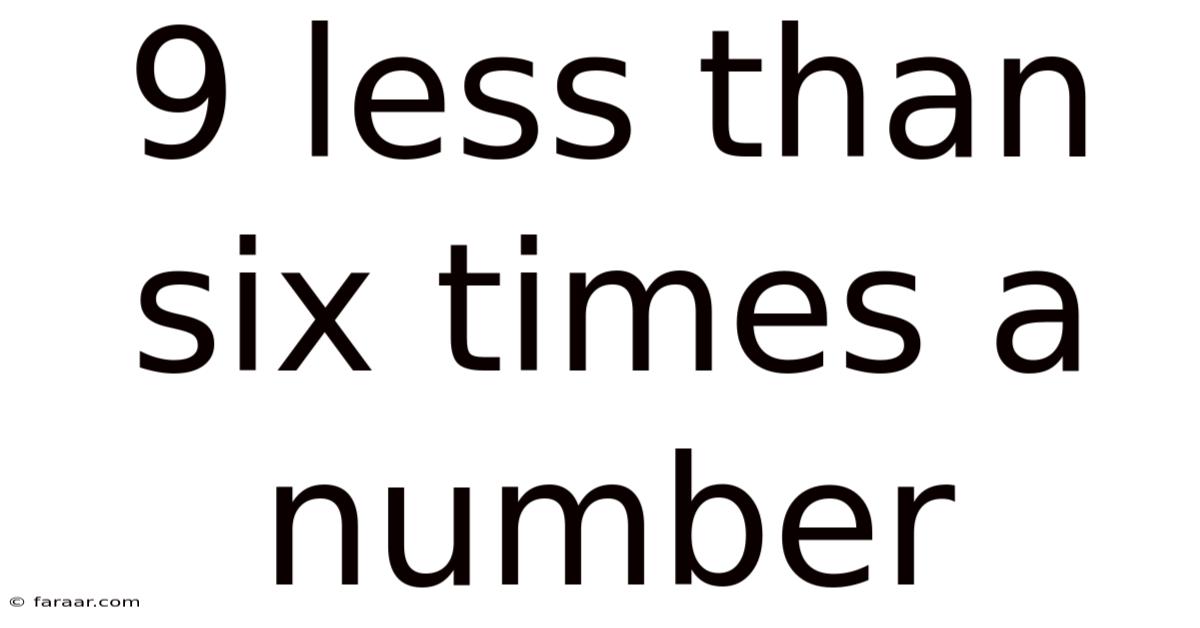
Table of Contents
Decoding "9 Less Than Six Times a Number": A Comprehensive Guide to Algebraic Expressions
This article explores the algebraic expression "9 less than six times a number," breaking down its meaning, demonstrating how to translate it into mathematical notation, and solving various problems based on this expression. We'll delve into the underlying concepts, providing a comprehensive guide suitable for students of all levels, from those just beginning their algebra journey to those looking to solidify their understanding of algebraic manipulation. This exploration will cover translating word problems into equations, solving equations, and understanding the importance of order of operations.
Introduction: Understanding the Language of Algebra
Algebra, at its core, is about using symbols and letters to represent unknown quantities. This allows us to express relationships and solve problems that would be difficult or impossible to solve using only arithmetic. The phrase "9 less than six times a number" is a classic example of a word problem that needs to be translated into algebraic notation. This translation process is crucial for solving any problem involving this expression. We'll learn how to break down this phrase step-by-step, identifying the key components and their mathematical representations.
Breaking Down the Phrase: Identifying Key Components
Let's dissect the phrase "9 less than six times a number" to understand its individual parts:
- "a number": This represents an unknown value, which we typically denote with a variable, often x.
- "six times a number": This translates directly to 6 multiplied by x, or 6x.
- "9 less than": This indicates subtraction. It means we're taking 9 away from something. Crucially, the order matters. "9 less than" implies that the subtraction of 9 occurs after the multiplication of 6 and x.
Translating into Algebraic Notation
Combining these elements, the phrase "9 less than six times a number" is correctly represented by the algebraic expression: 6x - 9. This expression uses the variable x to represent the unknown number, incorporates the multiplication ("six times"), and correctly represents the subtraction ("9 less than"). Understanding the order of operations (PEMDAS/BODMAS) is crucial here: multiplication (6x) is performed before subtraction (-9).
Solving Equations Involving the Expression
Now that we understand the algebraic representation, let's explore how to solve equations involving this expression. This will involve different scenarios, ranging from finding the value of x given the result of the expression to forming and solving equations based on contextual problems.
Scenario 1: Finding x Given the Value of the Expression
Let's say the expression 6x - 9 equals 21. To find the value of x, we set up and solve the equation:
6x - 9 = 21
-
Add 9 to both sides: This isolates the term with x. 6x - 9 + 9 = 21 + 9 6x = 30
-
Divide both sides by 6: This solves for x. 6x / 6 = 30 / 6 x = 5
Therefore, if "9 less than six times a number" is 21, then the number (x) is 5.
Scenario 2: Word Problems Involving the Expression
Let's consider a real-world example: "John earns six times as much as his brother, but after paying $9 in taxes, he has $21 left. How much does John's brother earn?"
-
Translate the problem into an algebraic equation: Let y represent the amount John's brother earns. John earns 6y. After taxes, John has 6y - 9 = 21.
-
Solve the equation: This equation is identical to the one we solved in Scenario 1. Following the same steps, we find that y = 5.
Therefore, John's brother earns $5.
Scenario 3: More Complex Equations
Let's consider a slightly more complex scenario: "The sum of '9 less than six times a number' and twice the number is 37. Find the number."
-
Translate the problem into an equation: The expression "9 less than six times a number" is 6x - 9. Twice the number is 2x. The sum of these is 37, so the equation is: (6x - 9) + 2x = 37
-
Simplify and solve: 8x - 9 = 37 8x = 46 x = 46/8 = 23/4 = 5.75
In this case, the number is 5.75.
Scenario 4: Inequalities Involving the Expression
We can also explore inequalities. For example, "9 less than six times a number is greater than 15". This translates to:
6x - 9 > 15
-
Add 9 to both sides: 6x > 24
-
Divide by 6: x > 4
This means that the number must be greater than 4.
Explanation of the Underlying Mathematical Principles
The problems above illustrate fundamental algebraic concepts:
- Variables: Using letters (like x or y) to represent unknown quantities.
- Expressions: Combinations of variables, numbers, and operations (like 6x - 9).
- Equations: Statements showing that two expressions are equal (e.g., 6x - 9 = 21).
- Inequalities: Statements comparing two expressions using inequality symbols (>, <, ≥, ≤).
- Order of Operations: The order in which operations are performed (PEMDAS/BODMAS). Multiplication and division are performed before addition and subtraction.
- Solving Equations: Manipulating equations to isolate the variable and find its value. This involves using inverse operations (addition/subtraction, multiplication/division).
Frequently Asked Questions (FAQ)
-
Q: What if the phrase was "six times a number less 9"?
- A: This would also be written as 6x - 9. The order of "less than" implies the subtraction happens after the multiplication.
-
Q: Can "9 less than six times a number" be written differently?
- A: While 6x - 9 is the most concise and accurate representation, you could also write it as 6x + (-9) to emphasize the addition of a negative number.
-
Q: What if the number is negative?
- A: The expression works perfectly with negative numbers. For instance, if x = -2, then 6x - 9 = 6(-2) - 9 = -12 - 9 = -21.
-
Q: How can I improve my skills in solving these types of problems?
- A: Practice is key! Work through various word problems, focusing on translating words into algebraic expressions and then solving the resulting equations or inequalities.
Conclusion: Mastering Algebraic Translations
Understanding how to translate word problems into algebraic expressions is a cornerstone of success in algebra and beyond. The phrase "9 less than six times a number," while seemingly simple, provides a rich opportunity to practice these crucial skills. By carefully breaking down the phrase, understanding the order of operations, and practicing solving different types of equations and inequalities, you can build a strong foundation in algebraic manipulation and confidently tackle more complex problems. Remember, the key is consistent practice and careful attention to detail. With dedication and practice, you can master the art of translating word problems into mathematical language and unlock the power of algebra.
Latest Posts
Latest Posts
-
How To Find An Equation Of A Line Parallel
Sep 12, 2025
-
How Many Real Solutions Does The System Of Equations Have
Sep 12, 2025
-
What Is The Probability Of Spinning An Even Number
Sep 12, 2025
-
Reading Tutoring For Kids Near Me
Sep 12, 2025
-
Why Dont Planets Fall Into The Sun
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 9 Less Than Six Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.