9 Is 36 Of What Number
faraar
Aug 26, 2025 · 5 min read
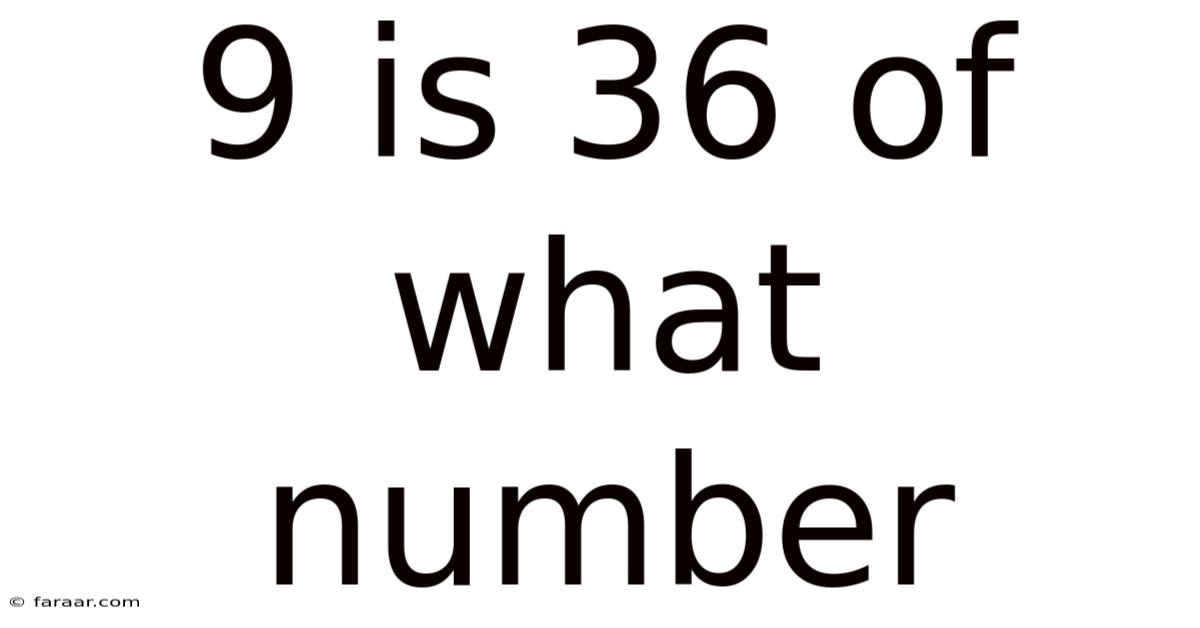
Table of Contents
9 is 36% of What Number? Unraveling the World of Percentages
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to analyzing financial data and understanding statistical information. This article will delve into the seemingly simple question, "9 is 36% of what number?", demonstrating various methods to solve this problem and expanding upon the broader concepts of percentage calculations. We'll explore different approaches, from basic algebraic solutions to more intuitive methods, ensuring a comprehensive understanding for all readers. By the end, you'll not only know the answer but also possess a solid foundation in percentage calculations.
Understanding the Problem: Deconstructing the Question
The question, "9 is 36% of what number?", essentially presents us with a percentage problem where we need to find the base value. We know the part (9) and the percentage (36%), and our goal is to determine the whole number. This type of problem frequently appears in various contexts, from simple arithmetic exercises to complex real-world applications in finance, statistics, and more. Let's break it down step-by-step to understand the underlying mathematical relationship.
Method 1: The Algebraic Approach
This method utilizes the fundamental formula for calculating percentages:
Part = Percentage × Whole
In our case:
- Part = 9
- Percentage = 36% = 0.36 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole = x (This is the unknown value we need to find)
Substituting these values into the formula, we get:
9 = 0.36x
To solve for x, we divide both sides of the equation by 0.36:
x = 9 / 0.36
x = 25
Therefore, 9 is 36% of 25.
Method 2: The Proportion Method
This method uses the concept of proportions to solve the problem. We can set up a proportion as follows:
9 / x = 36 / 100
Here, 9 represents the part, x represents the whole, 36 represents the percentage, and 100 represents the total percentage (100%). To solve this proportion, we can cross-multiply:
9 * 100 = 36 * x
900 = 36x
Now, divide both sides by 36:
x = 900 / 36
x = 25
Again, we find that 9 is 36% of 25.
Method 3: The Unitary Method
The unitary method focuses on finding the value of 1% first, then scaling it up to find the value of the whole.
If 36% of a number is 9, then 1% of that number would be:
9 / 36 = 0.25
Since 1% is 0.25, then 100% (the whole number) would be:
0.25 * 100 = 25
Thus, we arrive at the same answer: 9 is 36% of 25.
Method 4: Using a Calculator
Most modern calculators have a percentage function. You can use this function directly to solve the problem. While this is the quickest method, it's crucial to understand the underlying mathematical principles, as demonstrated in the previous methods. The process would generally involve using the inverse percentage function or a series of calculations to isolate the unknown value.
Practical Applications: Real-World Examples
Understanding percentage calculations like this one has numerous practical applications. Consider these examples:
- Sales and Discounts: A store offers a 36% discount on an item, and the discount amount is $9. Using the methods above, you can determine the original price of the item ($25).
- Financial Analysis: If a company's profits increased by 36% and the increase was $9 million, you can calculate the previous year's profit ($25 million).
- Statistical Data: In statistical analysis, understanding percentages is crucial for interpreting data, making comparisons, and drawing conclusions. This type of calculation would form the basis for many such analyses.
- Grade Calculations: If a student scored 9 points out of a possible 36, their percentage score would be 25%, representing the proportion of the total points achieved.
Expanding on Percentage Concepts: Beyond the Basics
While we've solved the initial problem, let's further explore the world of percentages:
- Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values, dividing it by the original value, and multiplying by 100%.
- Compound Interest: This involves calculating interest not only on the principal amount but also on accumulated interest. Understanding percentages is crucial for understanding how compound interest works over time.
- Proportional Reasoning: This is a broader mathematical concept that encompasses percentage calculations. It involves understanding the relationships between different quantities and using ratios and proportions to solve problems.
Frequently Asked Questions (FAQ)
Q: What if the percentage was greater than 100%?
A: If the percentage is greater than 100%, it means the "part" is larger than the "whole." This often arises in scenarios like population growth or investment returns exceeding the initial amount. The same mathematical principles apply; you would simply solve the equation as before.
Q: Can I use this method for other percentage problems?
A: Absolutely! The methods outlined above – algebraic, proportion, and unitary – are applicable to a wide range of percentage problems, regardless of the specific numbers involved. The key is to identify the known values (part and percentage) and the unknown value (whole) and apply the appropriate method.
Q: Are there any online tools or calculators that can help with this?
A: Yes, numerous online calculators and tools are readily available to assist with percentage calculations. These tools can often handle more complex scenarios and provide a quick solution, but it's still beneficial to understand the underlying mathematical concepts.
Conclusion: Mastering Percentages
This article explored the problem of finding the number of which 9 is 36%, utilizing multiple methods to arrive at the solution of 25. However, the true value lies not just in finding the answer but in grasping the fundamental principles of percentage calculations. By understanding these principles and the various approaches to solving percentage problems, you'll be equipped to handle a wide range of mathematical challenges in various real-world situations. Remember the core formula (Part = Percentage × Whole) and practice applying the different methods to solidify your understanding and build your confidence in tackling percentage problems. Mastering percentages is a crucial step towards becoming more proficient in mathematics and its numerous applications.
Latest Posts
Latest Posts
-
Give Exact Values Not Decimal Approximations
Aug 26, 2025
-
What Is 4 Percent Of 80
Aug 26, 2025
-
The Pythagorean Theorem Is Derived From The Distance Formula
Aug 26, 2025
-
Is 31 A Prime Number Or A Composite Number
Aug 26, 2025
-
How To Help My Son Read Better
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about 9 Is 36 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.