9 Is 25 Of What Number
faraar
Sep 16, 2025 · 5 min read
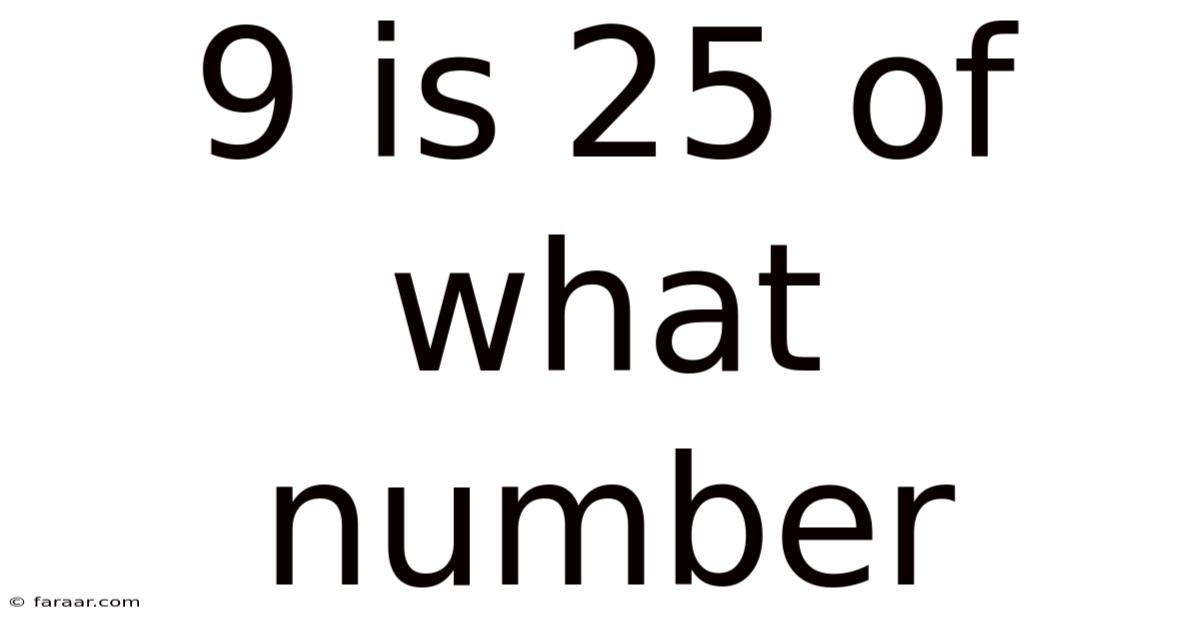
Table of Contents
9 is 25% of What Number? Unlocking the Power of Percentages
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing financial data and understanding statistical information. This article will delve into the seemingly simple question, "9 is 25% of what number?", providing a comprehensive explanation of the solution, exploring different approaches, and expanding upon the broader concept of percentage calculations. We'll equip you with the tools to confidently tackle similar problems and appreciate the versatility of percentages in various contexts.
Understanding the Problem: Breaking Down the Question
The core of the problem lies in translating the statement "9 is 25% of what number?" into a mathematical equation. The phrase "25% of what number" indicates an unknown value that, when multiplied by 25%, results in 9. This unknown value is what we need to find.
Method 1: Using the Percentage Formula
The most straightforward method involves using the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part: 9 (this is the portion we know)
- Percentage: 25% (or 0.25 as a decimal)
- Whole: This is the unknown value we need to determine (let's represent it with 'x')
Substituting these values into the formula, we get:
9 = 0.25 × x
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.25:
x = 9 ÷ 0.25
x = 36
Therefore, 9 is 25% of 36.
Method 2: Working with Fractions
Percentages can also be expressed as fractions. 25% is equivalent to 25/100, which simplifies to 1/4. We can rewrite the problem as:
9 = (1/4) × x
To solve for x, we multiply both sides by 4:
x = 9 × 4
x = 36
This method reinforces the connection between fractions and percentages, offering an alternative approach to reach the same solution.
Method 3: Using Proportions
Proportions offer another elegant way to solve percentage problems. We can set up a proportion:
9/x = 25/100
This proportion states that the ratio of 9 to the unknown number (x) is equal to the ratio of 25 to 100 (which represents 25%). To solve for x, we cross-multiply:
9 × 100 = 25 × x
900 = 25x
Divide both sides by 25:
x = 900 ÷ 25
x = 36
The proportional method highlights the relationship between the parts and the whole, providing a visual representation of the problem.
Expanding on Percentages: Key Concepts and Applications
The ability to solve problems like "9 is 25% of what number?" is crucial for understanding and applying percentages in numerous real-world situations. Let's explore some key concepts and applications:
-
Understanding Percentage Increase and Decrease: Percentages are frequently used to represent changes in quantities. For example, a 10% increase in price means the new price is 110% of the original price. Conversely, a 10% decrease means the new value is 90% of the original.
-
Calculating Discounts and Sales Tax: Retail stores often advertise discounts as percentages. If an item is 30% off, you're effectively paying 70% of its original price. Sales tax is added as a percentage of the purchase price.
-
Analyzing Financial Data: Percentages are essential for interpreting financial statements. Profit margins, interest rates, and rates of return are all expressed as percentages. Understanding these percentages helps make informed financial decisions.
-
Understanding Statistics and Probability: Percentages are widely used in statistics to represent proportions and probabilities. For instance, a survey might report that 60% of respondents prefer a certain product.
-
Converting Percentages to Decimals and Fractions: Fluency in converting between percentages, decimals, and fractions is vital for solving percentage problems efficiently. Remember that to convert a percentage to a decimal, divide by 100. To convert a decimal to a percentage, multiply by 100.
Real-World Examples: Applying Percentage Calculations
Let's illustrate how these concepts apply in real-world scenarios:
Scenario 1: Retail Discount
A shirt is on sale for $27, which is 75% of its original price. What was the original price?
Using the formula: Part = Percentage × Whole, we have:
27 = 0.75 × x
x = 27 ÷ 0.75
x = $36
The original price of the shirt was $36.
Scenario 2: Investment Return
An investment increased by 15% over a year, resulting in a profit of $1200. What was the initial investment amount?
The $1200 represents 15% of the original investment. Let's use the proportion method:
1200/x = 15/100
1200 × 100 = 15 × x
120000 = 15x
x = 120000 ÷ 15
x = $8000
The initial investment was $8000.
Frequently Asked Questions (FAQ)
Q1: What if the percentage is greater than 100%?
A percentage greater than 100% indicates that the part is larger than the whole. This often happens when representing growth or increases exceeding the original value. The same formulas apply; however, the solution will be a value larger than the given part.
Q2: How can I check my answer?
To verify your answer, plug the calculated value back into the original equation. If the equation holds true, your solution is correct. For example, in our initial problem, we found x = 36. Plugging this back in: 0.25 × 36 = 9. The equation is true, confirming our answer.
Q3: Are there any other methods to solve percentage problems?
Yes, various methods exist, including using ratios, proportions, and even algebraic manipulations depending on the complexity of the problem. The best method often depends on personal preference and the specifics of the problem.
Q4: What are some common mistakes to avoid when working with percentages?
Common mistakes include misinterpreting the problem, incorrectly converting percentages to decimals or fractions, and overlooking the order of operations. Always carefully read the problem and double-check your calculations.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a valuable life skill with far-reaching implications. By mastering the techniques and concepts presented in this article, you'll be well-equipped to tackle various percentage-related problems confidently. Whether you're calculating discounts, analyzing financial data, or interpreting statistical information, a strong grasp of percentages will enhance your ability to make informed decisions and succeed in many aspects of life. Remember the fundamental formula, explore different solution methods, and practice regularly to strengthen your understanding and build your mathematical proficiency. The ability to quickly and accurately calculate percentages is a skill that will serve you well throughout your academic and professional journeys.
Latest Posts
Latest Posts
-
How To Find The Volume Of A Half Circle
Sep 16, 2025
-
If A Dog Cell Has 72 Chromosomes
Sep 16, 2025
-
How Many Pounds Is 600 G
Sep 16, 2025
-
Find The Area Of The Region Bounded By The
Sep 16, 2025
-
How To Identify Zero Force Members In A Truss
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 9 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.