9 3 1 1/3 What's Next
faraar
Aug 25, 2025 · 5 min read
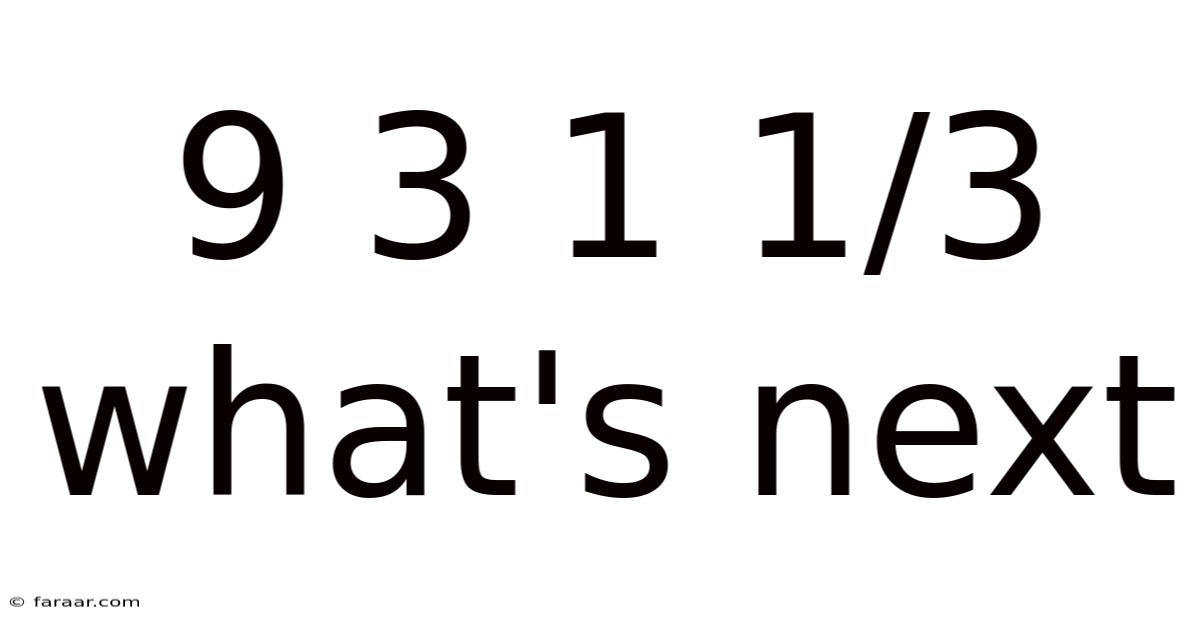
Table of Contents
Decoding the Sequence: 9, 3, 1, 1/3 – What Comes Next?
This article delves into the fascinating world of number sequences and explores the seemingly simple, yet intellectually stimulating, progression: 9, 3, 1, 1/3. We'll unravel the pattern behind this sequence, understand the underlying mathematical principles, and explore different approaches to predicting the next number. This journey will not only reveal the answer but also enhance your understanding of mathematical reasoning and pattern recognition.
Introduction: The Allure of Number Sequences
Number sequences are fundamental to mathematics, appearing in various fields from algebra and calculus to computer science and cryptography. They challenge us to identify underlying rules, develop logical thinking, and apply our mathematical knowledge. The sequence 9, 3, 1, 1/3 presents an excellent case study for exploring these principles. While seemingly straightforward, it introduces a subtle shift that requires careful observation and analysis. The ability to decipher such patterns is crucial for problem-solving across numerous disciplines.
Identifying the Pattern: Division by Three
The most apparent pattern in the sequence 9, 3, 1, 1/3 is the consistent division by three. Let's break it down:
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- 1 ÷ 3 = 1/3
This simple observation is the key to understanding the sequence. Each subsequent number is obtained by dividing the previous number by 3. This consistent operation forms the basis of a geometric progression.
Understanding Geometric Progressions
A geometric progression (or geometric sequence) is a sequence where each term is found by multiplying the previous term by a constant value, known as the common ratio. In our case, the common ratio is 1/3. This means we're dealing with a decreasing geometric progression, as the terms become smaller with each iteration. The formula for the nth term of a geometric progression is:
- a<sub>n</sub> = a<sub>1</sub> * r<sup>(n-1)</sup>
Where:
- a<sub>n</sub> is the nth term in the sequence
- a<sub>1</sub> is the first term in the sequence
- r is the common ratio
- n is the term number
Applying the Formula: Predicting the Next Number
Using the formula for a geometric progression, we can predict the next number in our sequence. In our case:
- a<sub>1</sub> = 9
- r = 1/3
- n = 5 (since we want to find the 5th term)
Therefore:
- a<sub>5</sub> = 9 * (1/3)<sup>(5-1)</sup> = 9 * (1/3)<sup>4</sup> = 9 * (1/81) = 1/9
Thus, the next number in the sequence is 1/9.
Extending the Sequence: Exploring Further Terms
We can continue extending the sequence using the same principle:
- 1/9 ÷ 3 = 1/27
- 1/27 ÷ 3 = 1/81
- 1/81 ÷ 3 = 1/243
And so on. The sequence continues infinitely, with each term becoming progressively smaller, approaching zero.
Beyond the Obvious: Alternative Perspectives
While the division by three is the most apparent pattern, it's crucial to explore alternative perspectives. Mathematical sequences can often exhibit multiple patterns or interpretations. While unlikely in this specific instance, considering other potential patterns helps develop a more holistic understanding. For instance, one might initially try adding or subtracting values, but this would not yield a consistent relationship throughout the sequence. The consistent nature of the division by 3 strongly suggests that it is the primary pattern at play.
Mathematical Explanation: Recursive Definition
The sequence can also be defined recursively. A recursive definition describes a sequence by specifying the first term and a rule for obtaining subsequent terms from the preceding ones. For this sequence, the recursive definition would be:
- a<sub>1</sub> = 9
- a<sub>n</sub> = a<sub>n-1</sub> / 3 for n > 1
This recursive definition clearly illustrates the process of repeatedly dividing by 3 to generate each subsequent term.
Real-World Applications: Geometric Progressions in Action
Geometric progressions, like the one demonstrated here, are not merely abstract mathematical concepts. They have numerous real-world applications. Examples include:
- Compound Interest: The growth of money invested with compound interest follows a geometric progression.
- Exponential Decay: The decay of radioactive materials, or the decrease in the value of an asset, can be modeled using geometric progressions.
- Population Growth/Decline: Under specific circumstances, population growth or decline can exhibit geometric progression-like characteristics.
- Computer Algorithms: Certain algorithms and data structures involve geometric progressions in their design and analysis.
Frequently Asked Questions (FAQ)
-
Q: Is there only one solution to this sequence? A: For this particular sequence, the consistent division by 3 points to a single, highly probable solution. While creatively exploring other potential patterns is encouraged for learning, the logical and consistent nature of the division by 3 makes it the most likely solution.
-
Q: What if the sequence started with a different number? A: The underlying principle of division by 3 would still apply. Changing the starting number would simply scale the entire sequence proportionally.
-
Q: Can this sequence be represented graphically? A: Yes, it can be represented graphically using a decreasing exponential curve.
Conclusion: The Power of Pattern Recognition
The sequence 9, 3, 1, 1/3, offers a concise yet powerful illustration of geometric progressions and the importance of pattern recognition in mathematics. By understanding the underlying principles, we can not only determine the next number in the sequence (1/9) but also extrapolate to future terms and appreciate the widespread applications of geometric progressions in various fields. This exercise highlights the intellectual satisfaction derived from solving mathematical puzzles and underscores the beauty of logical reasoning and pattern identification. The seemingly simple task of finding the next number in this sequence serves as a stepping stone to a deeper understanding of mathematical structures and their real-world applications. It encourages us to look beyond the surface, to seek underlying patterns, and to appreciate the elegance and power of mathematical thinking. The exploration of this sequence goes beyond a simple answer; it's an exploration of the fundamental principles that govern the world around us.
Latest Posts
Latest Posts
-
How Do You Find The Magnitude Of The Acceleration
Aug 25, 2025
-
J Is 14 Less Than 22
Aug 25, 2025
-
Homework 10 Projectile Motion And Quadratic Regression
Aug 25, 2025
-
Find The Value Of X In The Diagram
Aug 25, 2025
-
A Way To Start A Speech
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about 9 3 1 1/3 What's Next . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.