8 9 Divided By 2 3
faraar
Sep 23, 2025 · 6 min read
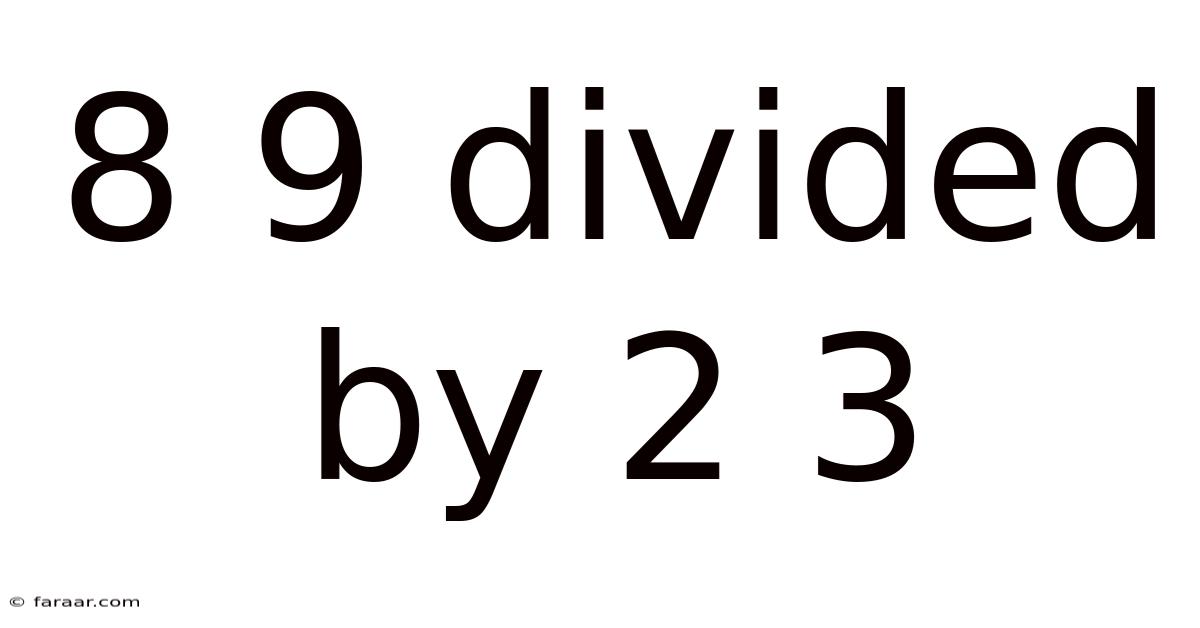
Table of Contents
Decoding the Math: A Deep Dive into 89 ÷ 23
This article explores the seemingly simple mathematical problem of 89 divided by 23, delving far beyond the immediate answer. We'll unpack the process using various methods, explaining the underlying mathematical concepts and providing insights into how to approach similar division problems with confidence. Understanding this seemingly simple calculation unlocks a deeper comprehension of arithmetic operations, crucial for more advanced mathematical endeavors.
Introduction: Why This Calculation Matters
At first glance, 89 ÷ 23 appears straightforward. However, this problem serves as a fantastic gateway to understanding fundamental arithmetic principles, including long division, estimation, and the concept of remainders. Mastering these concepts isn't just about solving this specific problem; it's about developing a robust mathematical foundation. This understanding extends to various real-world applications, from budgeting and cooking to engineering and computer science.
Method 1: Long Division – The Classic Approach
Long division is a tried-and-true method for solving division problems, especially when dealing with larger numbers. Let's break down 89 ÷ 23 step-by-step:
-
Setup: Write the problem in the standard long division format:
23 | 89 -
Estimate: How many times does 23 go into 89? A good estimation is crucial. Since 23 x 4 = 92 (slightly more than 89), let's try 3.
-
Multiply: Multiply the divisor (23) by our estimate (3): 23 x 3 = 69.
-
Subtract: Subtract the result (69) from the dividend (89): 89 - 69 = 20.
-
Remainder: The result (20) is our remainder. Since 20 is smaller than the divisor (23), we've reached the end of the long division process.
Therefore, 89 ÷ 23 = 3 with a remainder of 20. This can be expressed as 3 R20 or, more formally, as a mixed number: 3 20/23.
Method 2: Estimation and Approximation
Before jumping into complex calculations, estimation provides a quick way to get a sense of the answer's magnitude. Rounding numbers can simplify the process. We can round 23 to 20 and 89 to 90. 90 ÷ 20 = 4.5. This suggests our answer should be around 4, confirming our initial estimate in the long division method was reasonable, even if slightly lower. Estimation is a valuable skill, improving accuracy and reducing errors in more complex calculations.
Method 3: Repeated Subtraction
A less common but equally valid method is repeated subtraction. This involves subtracting the divisor (23) repeatedly from the dividend (89) until the result is less than the divisor.
- 89 - 23 = 66
- 66 - 23 = 43
- 43 - 23 = 20
We subtracted 23 three times before reaching a number (20) less than 23. This indicates that 89 ÷ 23 = 3 with a remainder of 20, mirroring our previous results. Repeated subtraction provides a concrete visualization of the division process, particularly beneficial for visual learners.
Understanding Remainders
The remainder (20 in this case) signifies the portion of the dividend that wasn't fully divisible by the divisor. In the context of 89 ÷ 23, it means that if we had 89 items to divide into groups of 23, we'd have 3 full groups and 20 items left over. Remainders are essential in many real-world applications, especially when dealing with discrete quantities. They highlight that division doesn't always result in a whole number.
Decimal Representation
The result can also be expressed as a decimal. To achieve this, we continue the division process beyond the remainder. We add a decimal point to the quotient (3) and a zero to the remainder (20), making it 200. We then continue the division:
- 200 ÷ 23. The closest whole number is 8 (23 x 8 = 184).
- Subtract: 200 - 184 = 16
- Add another zero: 160
- 160 ÷ 23 ≈ 6 (23 x 6 = 138)
- Subtract: 160 - 138 = 22
- Add another zero: 220 and so on.
This process can continue indefinitely, resulting in a non-terminating decimal. After several iterations, we get approximately 3.869565... Therefore, 89 divided by 23 is approximately 3.87. The accuracy of the decimal representation depends on how many decimal places are used.
Applications in Real-World Scenarios
Understanding division, including remainders and decimal representations, is crucial for various real-world scenarios:
- Sharing Resources: Dividing 89 candies among 23 children results in 3 candies per child with 20 candies remaining.
- Budgeting: If you need to spend $89 and each item costs $23, you can afford 3 items with $20 left over.
- Measurement: Converting units often involves division with remainders (e.g., converting inches to feet).
- Programming: Remainders are used in programming for tasks such as generating patterns and determining even/odd numbers.
Beyond the Basics: Exploring Related Concepts
This seemingly simple division problem opens doors to several more advanced mathematical concepts:
- Modular Arithmetic: The remainder (20) in 89 ÷ 23 is central to modular arithmetic, a branch of number theory with applications in cryptography and computer science.
- Fractions and Decimals: The mixed number representation (3 20/23) and the decimal approximation (3.87) highlight the relationship between fractions and decimals, crucial for understanding rational numbers.
- Algebraic Expressions: This problem could be represented algebraically as 89 = 23x + r, where 'x' is the quotient and 'r' is the remainder. Solving for 'x' and 'r' reinforces algebraic skills.
Frequently Asked Questions (FAQ)
-
Q: Why are there different methods for solving this problem? A: Different methods cater to different learning styles and provide different insights into the underlying mathematical processes. Some methods, like estimation, are faster, while others, like long division, are more systematic.
-
Q: Is there a single "correct" answer? A: While the whole number quotient (3) and the remainder (20) are fixed, the decimal representation can be rounded to different levels of accuracy.
-
Q: How do I know which method to use? A: The best method depends on the context and your comfort level. For quick estimations, rounding is useful. For precise answers, long division is recommended. Repeated subtraction can be helpful for visualizing the process.
-
Q: What if the numbers were much larger? A: The principles remain the same, although the calculations might become more tedious. Calculators and computer software are valuable tools for handling very large numbers.
Conclusion: Mastering Division, Mastering Math
The seemingly simple calculation of 89 ÷ 23 serves as a valuable learning experience. It highlights fundamental concepts in arithmetic, showcasing the importance of long division, estimation, remainders, and decimal representation. Understanding these concepts isn't merely about getting the correct answer; it's about developing a deeper understanding of mathematical processes that underpin countless real-world applications. By mastering the nuances of division, we build a strong foundation for more complex mathematical challenges ahead. The journey of understanding mathematics begins with such seemingly simple problems, progressively building toward a more comprehensive and fulfilling mathematical literacy.
Latest Posts
Latest Posts
-
Is The Oceanic Crust Denser Than The Continental
Sep 23, 2025
-
Which Of The Following Is An Example Of A Paradox
Sep 23, 2025
-
Which Sentence Correctly Uses Punctuation To Separate Coordinating Adjectives
Sep 23, 2025
-
Word Problems With Multi Step Equations
Sep 23, 2025
-
A Line That Intersects A Circle In Exactly One Point
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 8 9 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.