72 Is 80 Of What Number
faraar
Sep 19, 2025 · 4 min read
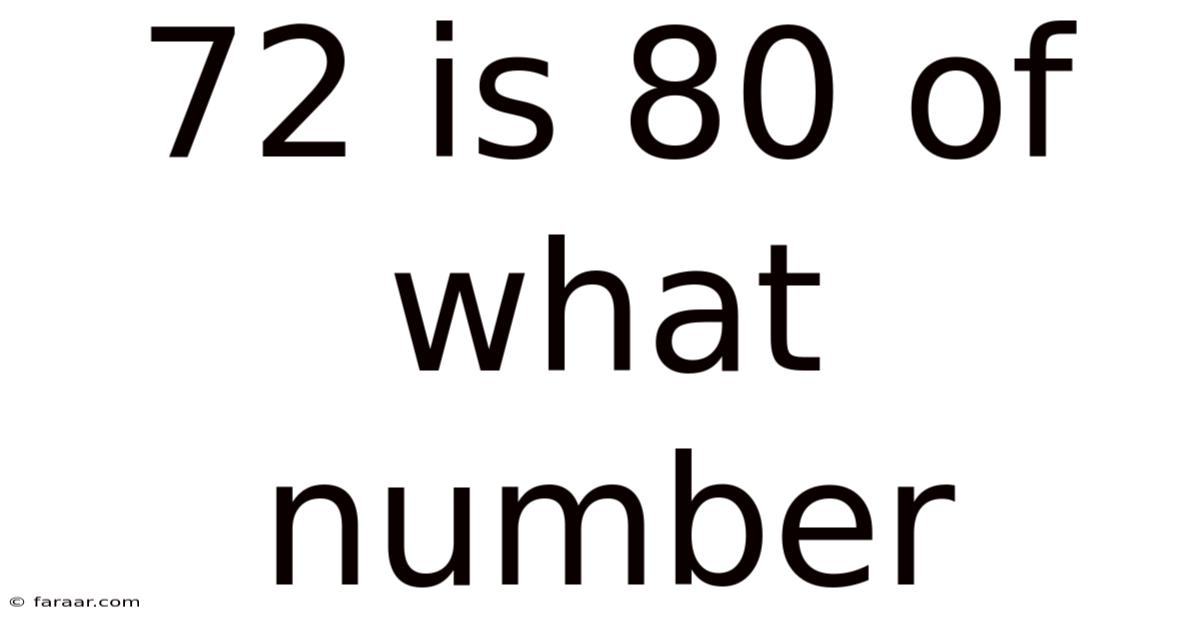
Table of Contents
72 is 80% of What Number? Unraveling the Mystery of Percentages
Finding a number when you know a percentage of it is a common problem encountered in various fields, from simple everyday calculations to complex financial modeling. This article will guide you through the process of solving the equation "72 is 80% of what number?", explaining the steps involved, the underlying mathematical principles, and providing practical examples to solidify your understanding. We'll also explore different methods to solve this type of percentage problem, ensuring you're equipped to tackle similar challenges confidently.
Understanding the Problem: Deconstructing the Percentage Equation
The core of this problem lies in understanding the relationship between a percentage, a part of a whole, and the whole itself. The statement "72 is 80% of what number?" can be translated into a mathematical equation:
72 = 0.80 * x
Where:
- 72 represents the part (80% of the unknown number).
- 0.80 (or 80/100) represents the percentage, expressed as a decimal.
- x represents the unknown number we're trying to find.
Method 1: Solving using Algebraic Manipulation
This is the most straightforward method, relying on basic algebraic principles. Our goal is to isolate 'x' on one side of the equation.
-
Rewrite the equation: We start with our equation: 72 = 0.80 * x
-
Divide both sides by 0.80: To isolate 'x', we need to divide both sides of the equation by 0.80. This maintains the balance of the equation.
72 / 0.80 = (0.80 * x) / 0.80
-
Simplify: This simplifies to:
x = 90
Therefore, 72 is 80% of 90.
Method 2: Using the Percentage Formula
The percentage formula provides a more structured approach to solving percentage problems. The formula is:
(Part / Whole) * 100% = Percentage
In our case, we know the part (72) and the percentage (80%). We need to find the whole (x). Let's substitute the known values:
(72 / x) * 100% = 80%
-
Simplify the equation: We can simplify this by dividing both sides by 100%:
72 / x = 0.80
-
Solve for x: Now, we can cross-multiply or rearrange the equation to solve for x:
72 = 0.80 * x x = 72 / 0.80 x = 90
Again, we arrive at the solution: x = 90
Method 3: Using Proportions
Proportions offer another effective method for solving percentage problems. We can set up a proportion based on the relationship between the part and the whole:
Part / Whole = Percentage / 100%
Substituting our known values:
72 / x = 80 / 100
-
Cross-multiply: Cross-multiplying gives us:
72 * 100 = 80 * x
-
Solve for x: Simplifying and solving for x:
7200 = 80x x = 7200 / 80 x = 90
Once more, the solution is x = 90.
Illustrative Examples: Applying the Concepts
Let's explore a few real-world examples to demonstrate the practical application of these methods:
-
Example 1: Sales Commission: A salesperson earns a commission of 80% on each sale. If they earned $72 in commission on a particular sale, what was the total value of that sale? Using the methods described above, the answer is $90.
-
Example 2: Grade Calculation: A student scored 72 points on a test, which represents 80% of the total possible points. What was the total number of points possible on the test? Again, the solution is 90 points.
-
Example 3: Discount Calculation: An item is on sale for $72 after an 80% discount. What was the original price of the item? In this case, $72 represents 20% (100% - 80%) of the original price. Applying the same principles, the original price was $360.
Explaining the Math: A Deeper Dive into Percentages
Percentages are essentially fractions expressed as a part of 100. When we say 80%, we mean 80 out of 100, or 80/100, which simplifies to 0.80 as a decimal. Understanding this fraction-to-decimal conversion is crucial in solving percentage problems. The methods outlined above all rely on this fundamental concept, manipulating the equation to isolate the unknown variable.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve these problems? A: Absolutely! Calculators are highly useful for performing the calculations, particularly when dealing with larger numbers or more complex percentages.
-
Q: What if the percentage is less than 100%? A: The methods remain the same. You'll still use the same equations and algebraic manipulations, just with a decimal representation of the percentage less than 1.
-
Q: What if the percentage is greater than 100%? A: This indicates that the "part" is larger than the "whole," often representing growth or increase. The mathematical processes are similar, but the result will be a number greater than the given "part."
Conclusion: Mastering Percentage Calculations
Solving percentage problems like "72 is 80% of what number?" may seem challenging at first, but with a clear understanding of the underlying concepts and the application of simple algebraic techniques, it becomes manageable. Whether you use algebraic manipulation, the percentage formula, or proportions, the key is to systematically translate the word problem into a mathematical equation and then solve for the unknown variable. By mastering these techniques, you'll gain a valuable skill applicable in numerous contexts, from everyday budgeting to advanced statistical analysis. Practice makes perfect; work through several examples to build your confidence and proficiency in tackling percentage problems.
Latest Posts
Latest Posts
-
How Big Is 20 Sq Meters
Sep 19, 2025
-
1 Teaspoon Sugar How Many Grams
Sep 19, 2025
-
Should The Comma Go Inside The Quotation Marks
Sep 19, 2025
-
How Do The Numbers On The Ph Scale Compare
Sep 19, 2025
-
The 3 Parts Of A Nucleotide Are A 5 Carbon
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 72 Is 80 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.