60 Of What Number Is 54
faraar
Aug 28, 2025 · 5 min read
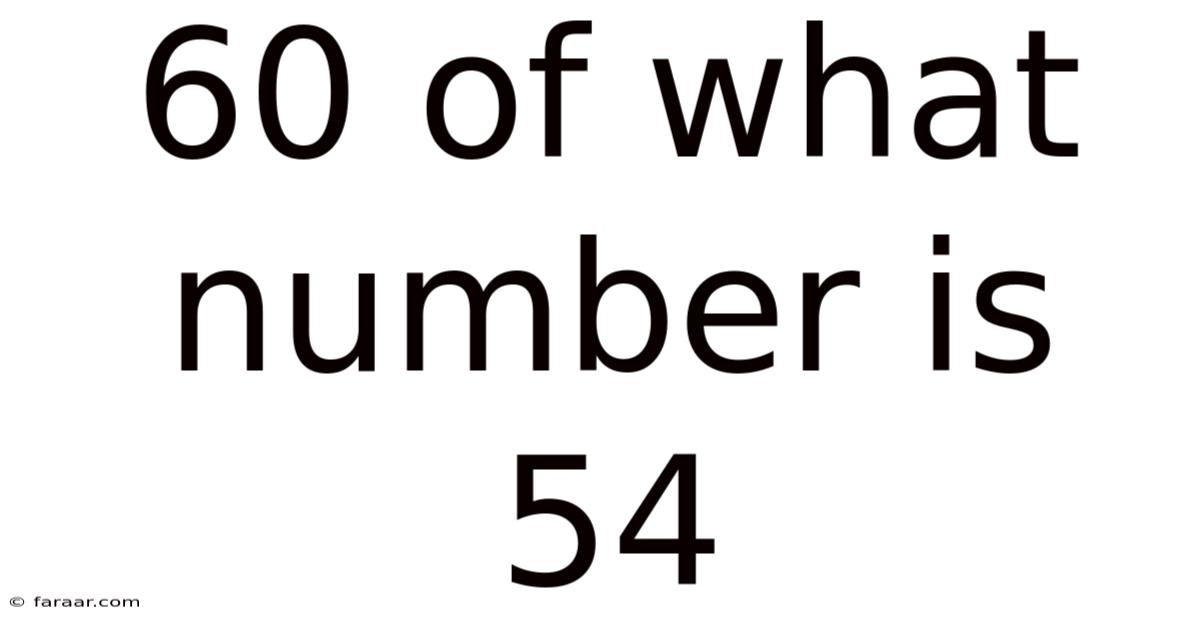
Table of Contents
Unveiling the Mystery: 60% of What Number is 54? A Deep Dive into Percentages and Problem-Solving
Finding the answer to "60% of what number is 54?" might seem like a simple math problem at first glance. However, understanding the underlying concepts and exploring different approaches to solving this problem opens a window into the world of percentages, ratios, and algebraic equations – crucial skills in many aspects of life. This article will not only provide the solution but also delve deeper into the methodologies, offering a comprehensive understanding of percentage calculations and their real-world applications.
Introduction: Understanding Percentages and Ratios
Percentages are a way of expressing a number as a fraction of 100. They're used extensively in everyday life, from calculating discounts and sales tax to understanding statistical data and financial reports. The core concept involves understanding the relationship between a part and a whole. A percentage represents the part relative to the whole, expressed as a portion of 100.
Ratios, on the other hand, express the relationship between two or more quantities. While percentages are always relative to 100, ratios can compare any two quantities. Understanding ratios is vital for solving percentage problems, as percentages can be expressed as ratios (e.g., 60% is equivalent to the ratio 60:100, or simplified to 3:5).
Method 1: Using the Equation Method (Algebra)
This method utilizes algebraic equations to solve for the unknown number. Let's represent the unknown number as 'x'. The problem "60% of what number is 54?" can be translated into the following equation:
0.60x = 54
To solve for 'x', we need to isolate it on one side of the equation. We can do this by dividing both sides by 0.60:
x = 54 / 0.60
x = 90
Therefore, 60% of 90 is 54.
Method 2: Using the Ratio Method (Proportion)
This method leverages the relationship between ratios. We know that 60% can be expressed as the ratio 60/100 or 3/5. We can set up a proportion to solve the problem:
3/5 = 54/x
To solve for 'x', we can cross-multiply:
3x = 5 * 54
3x = 270
x = 270 / 3
x = 90
Again, we arrive at the same answer: 60% of 90 is 54. This method highlights the interchangeable nature of percentages and ratios, emphasizing the core concept of proportional relationships.
Method 3: Using the Percentage Formula (Direct Calculation)
The basic percentage formula is:
Percentage = (Part / Whole) * 100
In our problem, we know the percentage (60%) and the part (54). We need to find the whole (x). Let's rearrange the formula:
Whole = (Part / Percentage) * 100
Substituting the values:
x = (54 / 60) * 100
x = 0.9 * 100
x = 90
Once more, the solution confirms that 60% of 90 equals 54. This method directly applies the fundamental percentage formula, reinforcing the core concepts involved.
Explanation: Why Does This Work?
The success of each method hinges on the underlying principle of proportional relationships. Whether you use an algebraic equation, ratios, or the direct percentage formula, you are essentially manipulating the relationship between the part (54), the whole (x), and the percentage (60%). The core idea is that these three values are intrinsically linked through a consistent proportional relationship.
The different methods simply offer various ways to express and solve this inherent relationship. The choice of method often depends on individual preference and the context of the problem. For complex problems involving multiple percentages or variables, the algebraic approach often provides a more structured and efficient solution.
Real-World Applications: Percentages in Everyday Life
Understanding percentage calculations is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all heavily rely on percentage calculations.
-
Sales and Marketing: Determining sales targets, analyzing market share, and calculating conversion rates all necessitate the use of percentages.
-
Science and Statistics: Analyzing data, interpreting experimental results, and expressing probability often involves percentages.
-
Everyday Shopping: Calculating discounts, comparing prices, and understanding value for money are all based on percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem?
- A: Absolutely! Calculators are excellent tools for performing percentage calculations efficiently. However, understanding the underlying methods is equally important to ensure you can solve similar problems without relying solely on a calculator.
-
Q: What if the percentage is not a whole number (e.g., 60.5%)?
- A: The methods described above work equally well with non-whole numbers. Simply substitute the decimal equivalent of the percentage (0.605 in this case) into the equation or ratio.
-
Q: Are there other ways to solve this type of percentage problem?
- A: Yes, there are other advanced mathematical techniques, particularly involving logarithms and exponential functions, that can also be applied to solve more complex percentage problems. However, the methods described above are sufficient for most everyday scenarios.
-
Q: What if I want to find what percentage 54 is of 90?
- A: This is a reverse percentage problem. You would use the formula: (Part / Whole) * 100 = Percentage. In this case, (54/90) * 100 = 60%.
Conclusion: Mastering Percentages for a Brighter Future
Solving the problem "60% of what number is 54?" is more than just finding the answer (90). It's about gaining a deeper understanding of percentages, ratios, and problem-solving techniques. These skills are essential for navigating various aspects of life, from personal finance and shopping to professional careers in fields that utilize mathematical analysis. By mastering these concepts, you equip yourself with valuable tools for critical thinking and effective problem-solving. The journey of understanding percentage calculations doesn't end with this single problem; it's the beginning of a broader exploration into the world of mathematics and its practical applications. Practice makes perfect, so continue exploring different percentage problems to solidify your understanding and build confidence in your abilities.
Latest Posts
Latest Posts
-
Books For Sophomores In High School
Aug 28, 2025
-
How To Find The C Value In A Sinusoidal Function
Aug 28, 2025
-
Calculate The Energy Of The Photon Emitted For Transition A
Aug 28, 2025
-
Maggi Buys 3 4 Pound Of Blueberries
Aug 28, 2025
-
A Pentagon With Two Right Angles
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about 60 Of What Number Is 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.