60 Is What Percent Of 75
faraar
Aug 28, 2025 · 5 min read
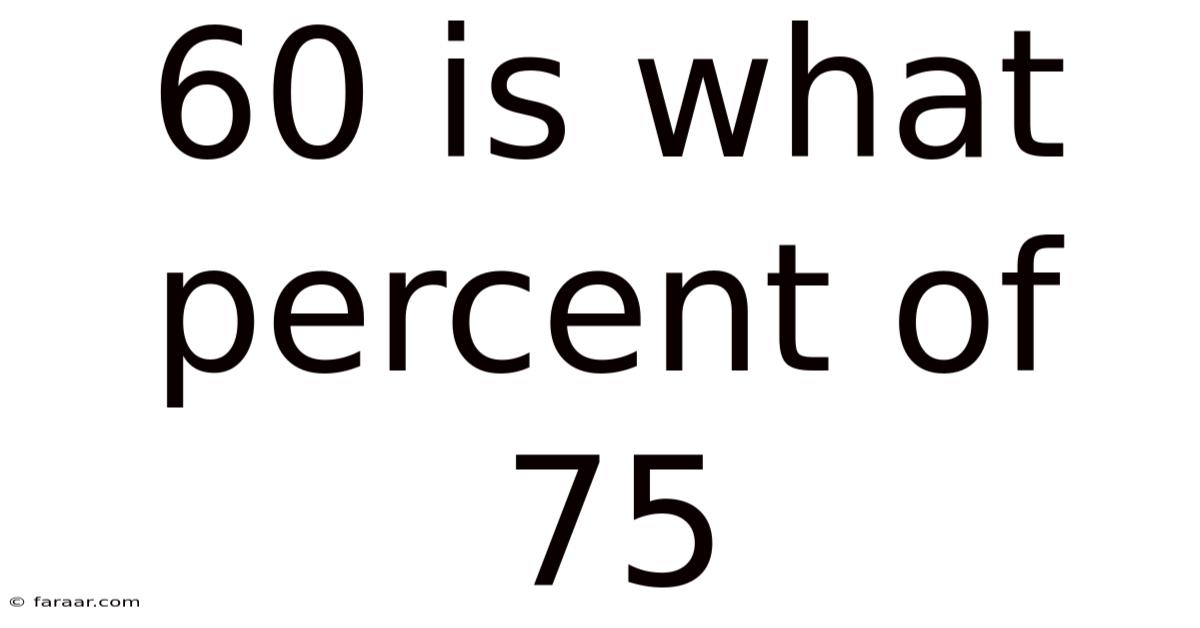
Table of Contents
60 is What Percent of 75? Understanding Percentages and Proportions
Calculating percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article will thoroughly explore how to determine what percentage 60 represents of 75, offering multiple approaches to solving this problem and expanding on the underlying concepts of percentages and proportions. We'll also delve into practical examples and address frequently asked questions to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" ( per centum in Latin). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Using the Percentage Formula
The most straightforward method to calculate what percentage 60 is of 75 is to use the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 60 (the number we want to express as a percentage)
- Whole: 75 (the total number)
Substituting these values into the formula:
(60 / 75) x 100% = 0.8 x 100% = 80%
Therefore, 60 is 80% of 75.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve for the unknown percentage (x):
60/75 = x/100
To solve for x, we can cross-multiply:
60 * 100 = 75 * x
6000 = 75x
x = 6000 / 75
x = 80
Therefore, x = 80%. This confirms our result from the previous method.
Method 3: Using Decimal Conversion
We can also solve this problem by first converting the fraction 60/75 into a decimal and then multiplying by 100% to express it as a percentage.
60/75 = 0.8
0.8 x 100% = 80%
This method demonstrates the direct relationship between decimals and percentages. Every decimal can be expressed as a percentage by multiplying by 100%.
Practical Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world situations. Here are a few examples:
- Sales and Discounts: If a store offers a 20% discount on an item originally priced at $75, you can calculate the discount amount and the final price using percentage calculations.
- Tax Calculations: Determining the amount of sales tax or income tax payable requires understanding percentages.
- Financial Analysis: Percentage changes in stock prices, interest rates, and other financial indicators are fundamental to investment decisions and economic analysis.
- Grade Calculations: Many grading systems rely on percentages to represent student performance. For instance, achieving 80% on a test often represents a high grade.
- Statistical Analysis: Percentages are frequently used to represent proportions and probabilities in statistical data analysis, helping to draw conclusions and make predictions.
Understanding Proportions in Depth
Proportions are a crucial mathematical concept closely linked to percentages. They express the relationship between two ratios. A ratio is a comparison of two quantities, often expressed as a fraction. For instance, the ratio of boys to girls in a class might be 3:2. Proportions are especially useful when dealing with problems involving scaling or comparing relative sizes.
In the problem "60 is what percent of 75," we essentially compare the ratio of 60 to 75 with the ratio of the unknown percentage (x) to 100. This forms the basis of our proportion: 60/75 = x/100.
Expanding on the Concept of Ratios
Ratios can be simplified just like fractions. For example, the ratio 60:75 can be simplified by dividing both numbers by their greatest common divisor (GCD), which is 15. Simplifying gives us the ratio 4:5. This means that for every 4 parts of one quantity, there are 5 parts of the other. Understanding ratio simplification helps in solving more complex percentage problems more efficiently.
Further Applications of Ratios and Proportions
Beyond percentages, ratios and proportions have numerous applications:
- Scaling Recipes: Adjusting the ingredients in a recipe to make a larger or smaller portion involves using ratios and proportions.
- Map Scales: Maps use ratios to represent distances on the ground compared to distances on the map.
- Model Building: Creating models of buildings, cars, or other objects involves using ratios and proportions to maintain accurate scaling.
- Engineering and Design: Engineers and designers frequently use ratios and proportions in various aspects of their work, from structural design to creating blueprints.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this type of problem?
A: Yes, absolutely! Calculators can quickly perform the necessary divisions and multiplications to determine the percentage. However, understanding the underlying principles is crucial for applying these calculations in different contexts and troubleshooting potential errors.
Q: What if I want to find what percentage 75 is of 60?
A: You would use the same formula, but the values of the 'Part' and 'Whole' would be reversed: (75/60) x 100% = 125%. This means 75 is 125% of 60.
Q: Are there other ways to solve percentage problems?
A: Yes, there are several other methods, including using the unitary method (finding the value of 1% and then multiplying) and using algebraic equations. The best method often depends on the specific problem and individual preference.
Conclusion
Determining that 60 is 80% of 75 is a straightforward calculation, but understanding the underlying concepts of percentages and proportions is essential for solving more complex problems. Mastering these concepts not only helps you solve mathematical problems efficiently but also equips you with vital skills applicable across various fields, from finance and statistics to everyday life situations. By understanding different methods of solving percentage problems and recognizing their practical applications, you can build a strong foundation in mathematical reasoning and problem-solving. Remember that practice is key to mastering percentage calculations, so try working through various examples to strengthen your skills.
Latest Posts
Latest Posts
-
An Angle Measures What Is The Measure Of Its Complement
Aug 29, 2025
-
What Is The Enthalpy Of Combustion Per Mole Of Butane
Aug 29, 2025
-
Net Ionic Equation For Acid Base Reaction
Aug 29, 2025
-
A Negative Divided By A Positive Is A
Aug 29, 2025
-
Finding The Equation Of A Secant Line
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about 60 Is What Percent Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.