6 More Than The Cube Of A Number.
faraar
Sep 13, 2025 · 6 min read
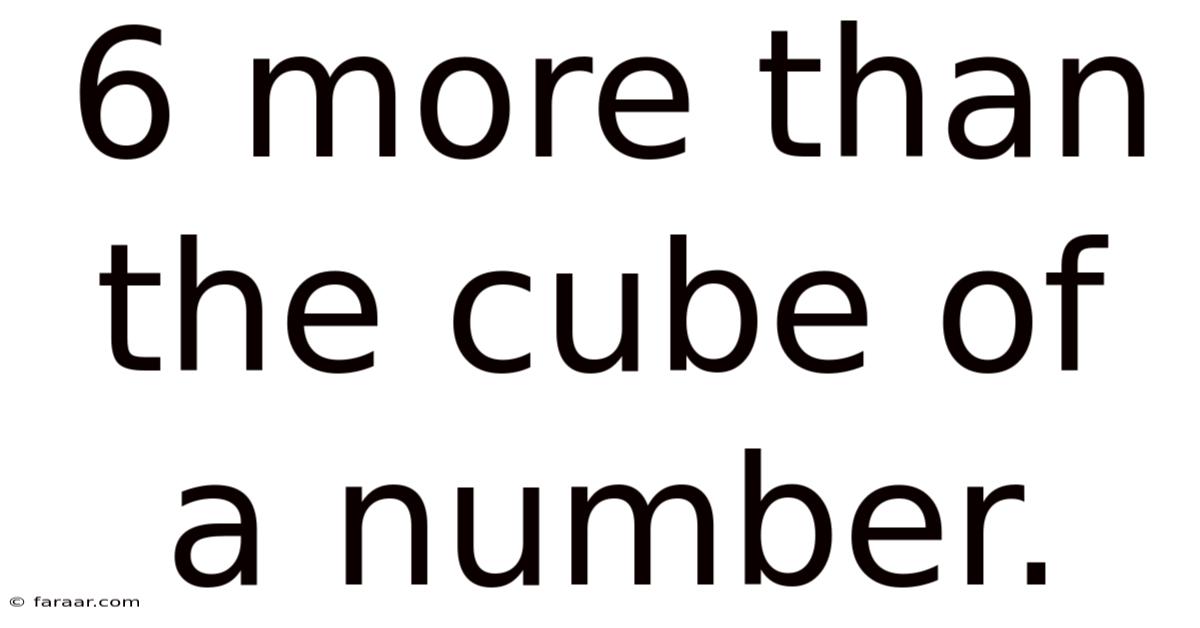
Table of Contents
6 More Than the Cube of a Number: Exploring Cubic Equations and Their Applications
This article delves into the mathematical expression "6 more than the cube of a number," exploring its representation, solving techniques for related cubic equations, and real-world applications. We will examine how this seemingly simple phrase translates into algebraic equations, the methods used to find solutions, and the significance of these solutions in various fields. Understanding this concept lays a crucial foundation for more advanced mathematical studies and problem-solving.
Understanding the Expression: From Words to Algebra
The phrase "6 more than the cube of a number" can be easily translated into algebraic notation. Let's represent the "number" with the variable x. The cube of this number is x³. Adding 6 to this gives us the expression x³ + 6. This simple algebraic representation is the key to unlocking a wide range of mathematical possibilities.
This expression forms the basis for various types of equations. For example, if we set this expression equal to a specific value, say y, we obtain a cubic equation: x³ + 6 = y. Solving this equation means finding the value(s) of x that satisfy the equation for a given y. The nature of the solutions – whether they are real numbers, complex numbers, or a combination of both – depends heavily on the value of y.
Solving Cubic Equations: Methods and Techniques
Solving cubic equations, like x³ + 6 = y, can be more challenging than solving linear or quadratic equations. There isn't one single, universally easy method, and the approach often depends on the specific form of the equation. Let's explore some common techniques:
1. Direct Solution by Subtraction:
The simplest scenario occurs when the equation is in the form x³ + 6 = y. To solve for x, we simply subtract 6 from both sides:
x³ = y - 6
Then, we take the cube root of both sides:
x = ³√(y - 6)
This method provides a direct solution, but it's only applicable when the equation is in this straightforward form. It also assumes we are looking for real number solutions.
2. Factoring:
If the cubic equation can be factored, solving becomes significantly easier. Factoring involves expressing the polynomial as a product of simpler expressions. For example, if our equation were x³ - x² - 6x = 0, we could factor it as:
x(x² - x - 6) = 0
This further factors to:
x(x - 3)(x + 2) = 0
The solutions are then x = 0, x = 3, and x = -2. However, this method relies on the cubic equation having easily identifiable factors, which is not always the case.
3. The Cubic Formula:
For general cubic equations of the form ax³ + bx² + cx + d = 0, a more complex solution method exists—the cubic formula. Similar to the quadratic formula for solving quadratic equations, the cubic formula provides a direct, albeit significantly more intricate, way to find the roots (solutions). The formula itself is quite lengthy and involves complex calculations, often requiring the use of numerical methods for approximation. While powerful, its complexity makes it less practical for hand calculations in most instances.
4. Numerical Methods:
For many cubic equations, particularly those that are not easily factored or have complex coefficients, numerical methods are often the most efficient approach. These methods involve iterative processes to approximate the roots of the equation. Common numerical methods include:
- Newton-Raphson Method: This iterative method refines an initial guess to approach a root with increasing accuracy.
- Bisection Method: This method repeatedly divides an interval containing a root in half, narrowing down the search until a desired level of accuracy is achieved.
- Secant Method: Similar to the Newton-Raphson method, but it approximates the derivative using the slope of a secant line.
These numerical techniques are crucial for solving complex cubic equations, often implemented using computer software or programming languages.
Real-World Applications of Cubic Equations
The concept of "6 more than the cube of a number," and the resulting cubic equations, has surprisingly broad applications in various fields:
1. Engineering and Physics:
Cubic equations frequently arise in solving problems related to:
- Fluid dynamics: Calculating fluid flow in pipes or channels often involves solving cubic equations.
- Structural mechanics: Analyzing the stresses and strains in structures sometimes leads to cubic equations.
- Electrical engineering: Designing circuits can involve solving cubic equations related to voltage and current relationships.
- Projectile motion: While often simplified to quadratic equations, more precise models of projectile motion may involve cubic equations to account for factors like air resistance.
2. Geometry:
Cubic equations can appear in geometric problems involving:
- Volumes of solids: Calculating the volume of certain three-dimensional shapes, especially those with non-uniform cross-sections, may require solving a cubic equation.
- Determining lengths and areas: Certain geometric constructions can lead to cubic relationships between dimensions.
3. Economics and Finance:
Cubic functions are sometimes used in:
- Modeling economic growth: Complex growth models may utilize cubic equations to capture non-linear relationships.
- Investment analysis: Certain investment models might employ cubic equations to represent the relationship between variables such as investment amount, time, and return.
4. Computer Graphics and Animation:
Cubic curves, defined by cubic equations, are commonly used in computer graphics and animation to create smooth and realistic curves for modeling shapes and creating animations. Bezier curves, for example, are widely used in these fields and are based on cubic polynomial functions.
Frequently Asked Questions (FAQs)
Q1: Can a cubic equation have more than one solution?
A1: Yes, a cubic equation can have up to three real solutions, but it may also have complex solutions (involving the imaginary unit i). The number of real solutions depends on the specific coefficients of the equation.
Q2: Are there any shortcuts for solving specific types of cubic equations?
A2: While the cubic formula works for all cubic equations, certain types of equations might offer shortcuts. For example, if the equation is easily factorable, factoring is a much simpler method. Recognizing patterns and special forms can significantly reduce the effort required to find solutions.
Q3: What if I get a negative value under the cube root?
A3: If you obtain a negative value under the cube root while solving a cubic equation using the direct method (³√(y - 6)), this indicates the existence of a real negative solution. The cube root of a negative number is a real number; for example, ³√(-8) = -2.
Q4: How can I solve cubic equations if I don’t have a calculator or computer?
A4: For simple cubic equations, direct subtraction and factoring are feasible. However, for more complex equations without readily available computational tools, numerical methods become extremely challenging to implement by hand. Approximation techniques might yield an estimate, but precise solutions would be difficult to obtain manually.
Q5: Are there any online tools or software packages available to solve cubic equations?
A5: Many online calculators and mathematical software packages (like MATLAB, Mathematica, or specialized online tools) are available that can efficiently solve cubic equations, often employing numerical methods for more complex cases.
Conclusion: The Significance of Cubic Equations
The seemingly simple phrase "6 more than the cube of a number" opens up a world of mathematical possibilities. Understanding how to translate this phrase into algebraic notation, the different techniques available for solving resulting cubic equations, and their wide-ranging applications in various disciplines emphasizes the importance of this fundamental mathematical concept. Whether tackling straightforward equations or complex problems in engineering, physics, or other fields, a solid grasp of cubic equations and their solutions is essential for successful problem-solving and deeper mathematical comprehension. The journey from simple words to complex solutions highlights the power and beauty of mathematics and its influence across diverse aspects of our world.
Latest Posts
Latest Posts
-
Can You Use Calculator On Ged
Sep 13, 2025
-
How To Tell If A Triangle Is Acute
Sep 13, 2025
-
What Is The Difference Between Literal Language And Figurative Language
Sep 13, 2025
-
How Big Is 200 Square Meters
Sep 13, 2025
-
Find The Quotient And Remainder Using Synthetic Division
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 6 More Than The Cube Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.