6 Divided By 1 1 2
faraar
Aug 25, 2025 · 5 min read
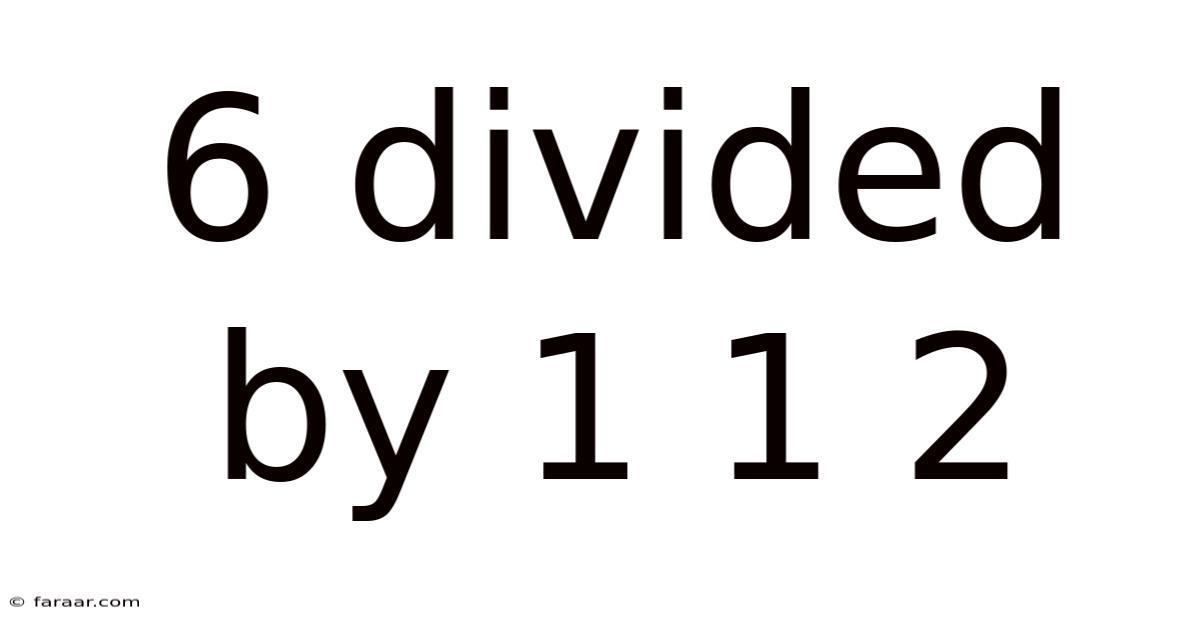
Table of Contents
Decoding 6 Divided by 1 1/2: A Comprehensive Guide
Dividing fractions and mixed numbers can seem daunting, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will thoroughly explain how to solve 6 divided by 1 1/2, providing a step-by-step guide, exploring the underlying mathematical concepts, and answering frequently asked questions. Understanding this seemingly simple problem unlocks a deeper understanding of fraction manipulation and lays the groundwork for more complex mathematical operations. The keywords throughout this article will include division, fractions, mixed numbers, improper fractions, and reciprocals.
Understanding the Problem: 6 ÷ 1 1/2
Before diving into the solution, let's break down the problem: 6 ÷ 1 1/2. This represents six whole units being divided into groups of one and a half units each. The goal is to determine how many groups of 1 1/2 can be formed from 6. This requires converting the mixed number into an improper fraction and then applying the rules of fraction division.
Step-by-Step Solution
Step 1: Convert the Mixed Number to an Improper Fraction
The first step involves converting the mixed number 1 1/2 into an improper fraction. A mixed number combines a whole number and a fraction. To convert it, we multiply the whole number (1) by the denominator of the fraction (2), add the numerator (1), and keep the same denominator.
1 1/2 = (1 * 2 + 1) / 2 = 3/2
Now our problem becomes 6 ÷ 3/2.
Step 2: Convert the Whole Number to a Fraction
To divide fractions, it's helpful to express all numbers as fractions. We can represent the whole number 6 as a fraction by placing it over 1: 6/1. Therefore, our problem is now: 6/1 ÷ 3/2
Step 3: Apply the Rule of Fraction Division
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by switching the numerator and the denominator. The reciprocal of 3/2 is 2/3.
So, 6/1 ÷ 3/2 becomes 6/1 * 2/3
Step 4: Multiply the Fractions
Now we simply multiply the numerators together and the denominators together:
(6 * 2) / (1 * 3) = 12/3
Step 5: Simplify the Result
The fraction 12/3 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 3:
12/3 = 4
Therefore, 6 divided by 1 1/2 equals 4.
Visualizing the Solution
Imagine you have 6 pizzas, and you want to divide them into servings of 1 1/2 pizzas each. You can clearly see that you can make four servings of 1 1/2 pizzas from 6 pizzas. This visual representation reinforces the numerical solution.
The Mathematical Explanation: Reciprocals and Division
The core principle behind dividing fractions lies in the concept of reciprocals. When we divide by a fraction, we are essentially asking, "How many times does this fraction fit into the whole number or other fraction?" Multiplying by the reciprocal provides the answer. This is because division is the inverse operation of multiplication.
Let's consider a simpler example: 1/2 ÷ 1/4. This asks, "How many 1/4s are there in 1/2?" Visually, we can see that there are two 1/4s in 1/2. Multiplying 1/2 by the reciprocal of 1/4 (which is 4/1 or 4) gives us: (1/2) * (4/1) = 4/2 = 2. This confirms our visual observation.
The same principle applies to our original problem, 6 ÷ 1 1/2. We convert to fractions, find the reciprocal, multiply, and simplify to arrive at the answer, 4.
Working with Different Units
The concept of division with mixed numbers extends beyond simple numerical problems. Consider a scenario where you have 6 meters of fabric, and each garment requires 1.5 meters. Applying the same method, you'd find you can make 4 garments. The underlying mathematical principle remains consistent regardless of the units involved. This versatility underscores the power of understanding fraction division.
Expanding the Concept: More Complex Problems
The techniques discussed here can be applied to more complex problems involving multiple fractions and mixed numbers. The key is always to:
- Convert mixed numbers to improper fractions.
- Convert whole numbers to fractions (numerator over 1).
- Find the reciprocal of the divisor (the number you are dividing by).
- Multiply the fractions.
- Simplify the result.
This systematic approach ensures accuracy and efficiency when solving any division problem involving fractions and mixed numbers.
Frequently Asked Questions (FAQ)
Q1: Why do we use reciprocals when dividing fractions?
A1: Dividing by a fraction is equivalent to multiplying by its reciprocal because division and multiplication are inverse operations. Multiplying by the reciprocal essentially "flips" the division problem into a multiplication problem that is easier to solve.
Q2: Can I solve this problem using decimals instead of fractions?
A2: Yes, you can. 1 1/2 is equivalent to 1.5. Therefore, the problem becomes 6 ÷ 1.5 = 4. Using decimals can be quicker for some, but understanding the fraction method provides a more fundamental grasp of the mathematical concepts involved.
Q3: What if I have a larger or smaller number being divided by 1 1/2?
A3: The method remains the same. Regardless of the size of the dividend (the number being divided), you would follow the steps outlined above: convert to fractions, find the reciprocal, multiply, and simplify.
Q4: Are there any other methods to solve this type of problem?
A4: While the method described above is the most common and generally efficient, you could also visually represent the problem (as with the pizza example) or use long division, though long division with fractions is less straightforward. The fraction method remains the most mathematically sound and widely applicable approach.
Conclusion: Mastering Fraction Division
Understanding how to solve 6 divided by 1 1/2 isn't merely about getting the correct answer (which is 4). It's about grasping the fundamental principles of fraction manipulation, reciprocals, and the relationship between division and multiplication. This understanding forms the basis for tackling more complex mathematical problems involving fractions and lays a solid foundation for advanced mathematical studies. Mastering this seemingly simple problem unlocks a wealth of mathematical possibilities. By consistently practicing and applying these principles, you will build confidence and proficiency in working with fractions, a crucial skill in various fields of study and practical applications.
Latest Posts
Latest Posts
-
How To Write Complex Numbers In Standard Form
Aug 25, 2025
-
How Do You Find The Magnitude Of The Acceleration
Aug 25, 2025
-
J Is 14 Less Than 22
Aug 25, 2025
-
Homework 10 Projectile Motion And Quadratic Regression
Aug 25, 2025
-
Find The Value Of X In The Diagram
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.