59 8 As A Mixed Number.
faraar
Sep 17, 2025 · 6 min read
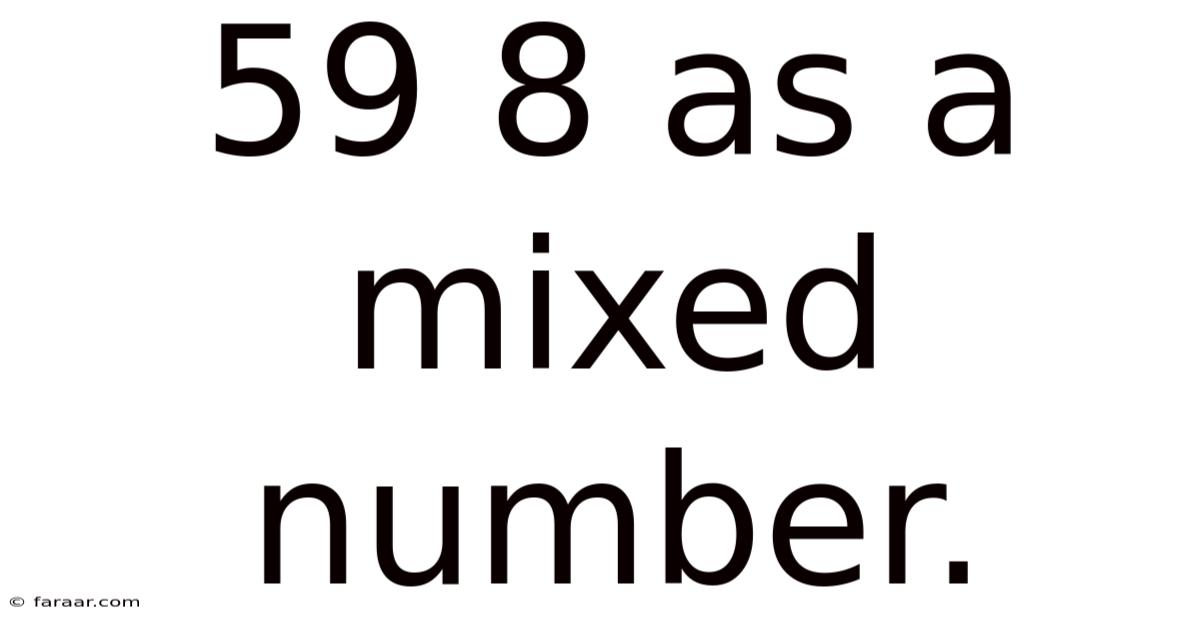
Table of Contents
Converting 59/8 to a Mixed Number: A Comprehensive Guide
Understanding how to convert improper fractions, like 59/8, into mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 59/8 but will also delve into the underlying principles, provide practical examples, and explore the broader context of working with fractions. This article aims to equip you with a thorough understanding of this essential mathematical concept, making it easy to understand and apply in various situations.
Introduction: Understanding Fractions and Mixed Numbers
Before we dive into the conversion of 59/8, let's clarify the terminology. A fraction represents a part of a whole. It's composed of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator tells you how many equal parts the whole is divided into, while the numerator indicates how many of those parts you have.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 59/8). This indicates you have more than one whole.
A mixed number combines a whole number and a proper fraction (e.g., 7 3/8). It represents a quantity that is greater than one. Converting improper fractions to mixed numbers is a way to express the same value in a more easily understandable format.
Converting 59/8 to a Mixed Number: Step-by-Step Guide
The process of converting an improper fraction to a mixed number involves dividing the numerator by the denominator. Here's how to convert 59/8:
Step 1: Divide the numerator by the denominator.
Divide 59 by 8. This can be done using long division:
7
8 | 59
-56
3
Step 2: Identify the whole number.
The quotient (the result of the division) is 7. This represents the whole number part of our mixed number.
Step 3: Identify the remainder.
The remainder is 3. This represents the numerator of the fractional part of our mixed number.
Step 4: Construct the mixed number.
The denominator of the fractional part remains the same as the original denominator (8). Therefore, the mixed number is 7 3/8.
This means that 59/8 is equivalent to 7 and 3/8. You have seven whole units and three-eighths of another unit.
Visualizing the Conversion: A Practical Example
Imagine you have 59 equally sized pieces of pizza. Each whole pizza is cut into 8 slices. To determine how many whole pizzas you have and how many slices are left over, we perform the conversion:
- Divide the total number of slices (59) by the number of slices per pizza (8).
- The quotient (7) represents the number of complete pizzas.
- The remainder (3) represents the number of slices left over, which is 3/8 of a pizza.
Therefore, you have 7 whole pizzas and 3/8 of a pizza left, perfectly illustrating the mixed number 7 3/8.
Converting Mixed Numbers Back to Improper Fractions
It's useful to understand the reverse process as well. Let's say we want to convert the mixed number 7 3/8 back to an improper fraction. Here's how:
Step 1: Multiply the whole number by the denominator.
7 x 8 = 56
Step 2: Add the numerator.
56 + 3 = 59
Step 3: Keep the denominator the same.
The denominator remains 8.
Step 4: Construct the improper fraction.
The resulting improper fraction is 59/8. This demonstrates the equivalence between the mixed number and the improper fraction.
The Importance of Understanding Mixed Numbers
Understanding mixed numbers is crucial for several reasons:
-
Real-world applications: Many everyday scenarios involve quantities that are greater than one but not a whole number. Think about measuring ingredients for a recipe (e.g., 2 1/2 cups of flour), measuring lengths (e.g., 3 3/4 inches), or dividing resources amongst people.
-
Simplification of calculations: Mixed numbers often provide a more intuitive and manageable format for calculations compared to improper fractions, particularly when adding, subtracting, multiplying, or dividing fractions.
-
Foundation for advanced mathematics: A strong grasp of fractions and mixed numbers forms the basis for understanding more complex mathematical concepts such as decimals, percentages, ratios, and proportions.
Further Exploration: Working with Other Improper Fractions
The process outlined above applies universally to converting any improper fraction to a mixed number. Let's consider some other examples:
-
17/5: Dividing 17 by 5 gives a quotient of 3 and a remainder of 2. Thus, 17/5 = 3 2/5.
-
23/4: Dividing 23 by 4 gives a quotient of 5 and a remainder of 3. Thus, 23/4 = 5 3/4.
-
31/6: Dividing 31 by 6 gives a quotient of 5 and a remainder of 1. Thus, 31/6 = 5 1/6.
These examples highlight the consistent application of the division process to obtain the whole number and fractional parts of the mixed number.
Frequently Asked Questions (FAQ)
Q1: What if the remainder is 0?
A1: If the remainder is 0, it means the improper fraction is a whole number. For example, 16/4 = 4, where the quotient is 4 and the remainder is 0. There is no fractional part in the mixed number.
Q2: Can I convert any fraction to a mixed number?
A2: No. Only improper fractions (where the numerator is greater than or equal to the denominator) can be converted to mixed numbers. Proper fractions (where the numerator is less than the denominator) cannot be converted to mixed numbers because they represent less than one whole unit.
Q3: Is there a faster way to convert improper fractions to mixed numbers?
A3: While the long division method is thorough and easy to understand, with practice you may find it quicker to perform the division mentally. Understanding the underlying principles allows for efficient calculations.
Q4: Why is it important to learn this conversion?
A4: This conversion is crucial for understanding and working with fractions in various mathematical applications. It provides a more manageable representation of quantities exceeding one unit and is essential for future mathematical learning.
Conclusion: Mastering Fraction Conversion
Converting improper fractions to mixed numbers is a core skill in arithmetic with broad applications in daily life and advanced mathematical studies. By understanding the underlying principle of division and applying the step-by-step process, you can confidently convert any improper fraction to its equivalent mixed number representation. This skill simplifies calculations and allows for a more intuitive understanding of quantities represented by fractions. Remember to practice regularly to build proficiency and solidify your understanding of this essential mathematical concept. The more you practice, the quicker and more comfortable you will become with converting fractions and working with mixed numbers.
Latest Posts
Latest Posts
-
Dilation By A Scale Factor Of 3
Sep 17, 2025
-
1 4 Divided By 3 In Fraction
Sep 17, 2025
-
What Happens When Kcl Is Dissolved In Water
Sep 17, 2025
-
Rewrite The Equation In Terms Of U
Sep 17, 2025
-
Pre Algebra Math Problems And Answers
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 59 8 As A Mixed Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.