5 X 2 3 4x 5
faraar
Sep 06, 2025 · 6 min read
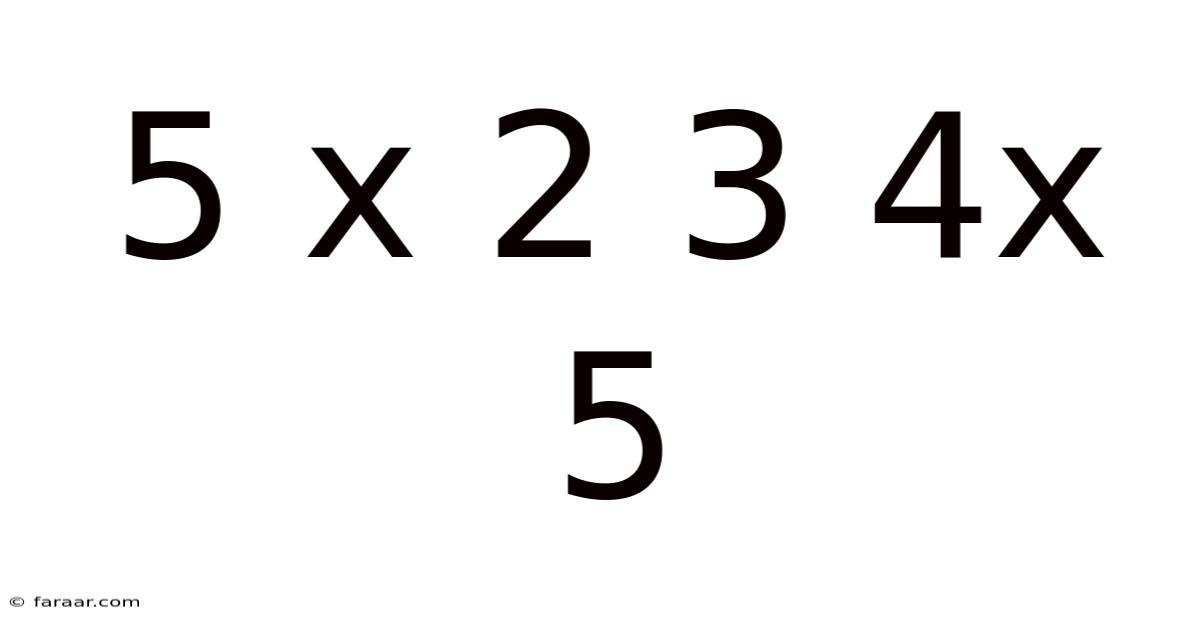
Table of Contents
Decoding the Mathematical Enigma: 5 x 2 3 4 x 5
This article delves into the seemingly simple yet surprisingly complex mathematical expression: 5 x 2 3 4 x 5. At first glance, it might appear straightforward, but the lack of explicit operators introduces ambiguity and opens the door to exploring different interpretations and the crucial role of the order of operations (PEMDAS/BODMAS). We will unravel this expression, exploring various possible solutions and the underlying mathematical principles. Understanding this will enhance your comprehension of fundamental arithmetic and the importance of precise notation.
Introduction: The Ambiguity of Implicit Operations
The expression "5 x 2 3 4 x 5" presents a challenge due to its implicit nature. The absence of clearly defined operators (+, -, ×, ÷) between the numbers leaves room for multiple interpretations. This ambiguity highlights the critical importance of using parentheses or other unambiguous notation when writing mathematical expressions. Without explicit operators, different individuals might interpret the expression differently, leading to varying results. This is why understanding the order of operations is paramount.
Order of Operations: PEMDAS/BODMAS
To resolve the ambiguity, we must apply the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same fundamental principle: operations are performed in a specific order. Let's break it down:
-
Parentheses/Brackets: Calculations within parentheses or brackets are performed first. Since our expression lacks parentheses, we move to the next step.
-
Exponents/Orders: Exponents (powers) are evaluated next. Again, our expression doesn't involve exponents.
-
Multiplication and Division: Multiplication and division are performed from left to right. This is where the interpretation becomes crucial in our expression.
-
Addition and Subtraction: Finally, addition and subtraction are carried out from left to right.
Possible Interpretations and Solutions
Given the absence of parentheses and exponents, we can explore several plausible interpretations based on different assumptions about the implicit operations:
Interpretation 1: All Multiplications
The simplest interpretation assumes all the spaces represent multiplication. In this case, the expression becomes:
5 × 2 × 3 × 4 × 5 = 600
This interpretation prioritizes multiplication as the only operation present and performs it sequentially from left to right. This yields a straightforward and easily calculable result.
Interpretation 2: Grouping based on proximity
Another approach involves grouping numbers based on their proximity. One might interpret the expression as:
(5 × 2) (3 × 4) × 5 = 10 × 12 × 5 = 600
This interpretation groups the numbers into pairs based on their adjacency. It still leads to the same result as Interpretation 1, highlighting that the sequential order of multiplication might yield the same result despite differences in grouping.
Interpretation 3: Introducing Implicit Addition
Let’s explore the possibility of implicit addition. This would require rewriting the expression with assumed plus signs. For example:
5 + 2 + 3 + 4 + 5 = 19
Or we could try a combination of multiplication and addition, leading to an array of different solutions. The variability emphasizes the critical need for explicit notation.
Interpretation 4: Alternative Grouping Strategies
Various groupings are possible. For instance:
5 × (2 + 3 + 4) × 5 = 5 × 9 × 5 = 225
or
5 × (2 × 3 × 4 × 5) = 5 × 120 = 600
These demonstrate that the absence of explicit operators renders the expression susceptible to multiple valid interpretations, depending on how the implicit operations are understood.
The Importance of Explicit Notation in Mathematics
The ambiguity of the expression "5 x 2 3 4 x 5" underscores the critical importance of precise mathematical notation. Ambiguous expressions can lead to misinterpretations, errors, and inconsistencies. Using parentheses, brackets, and explicitly stating all operators prevents confusion and ensures that the intended mathematical operation is correctly understood. Good mathematical notation is crucial for clear communication and avoids ambiguity. Mathematical conventions are not arbitrary; they are designed to facilitate unambiguous expression and correct interpretation.
Advanced Considerations: Beyond Basic Arithmetic
While the examples above focus on basic arithmetic, the principles of order of operations extend to more complex mathematical expressions involving exponents, roots, logarithms, and other functions. In such cases, adhering strictly to the order of operations becomes even more crucial to ensure accurate calculations. The use of parentheses or brackets remains essential to guide the order of operations explicitly. For example, in expressions involving multiple levels of parentheses, the innermost parentheses are evaluated first, then the next outer layer, and so on.
Illustrative Examples with Explicit Notation
To illustrate the importance of explicit notation, let's rewrite the ambiguous expression with clearly defined operators:
- Example 1: (5 × 2) × (3 × 4) × 5 = 600
- Example 2: 5 × (2 + 3 + 4) × 5 = 225
- Example 3: 5 × 2 × 3 × 4 × 5 = 600
- Example 4: 5 × (2 × (3 + 4)) × 5 = 175
These examples show that even with simple numbers, the use of brackets or parentheses significantly alters the order of operations, producing drastically different results. Always prioritize clarity and explicitness in your mathematical writing.
Frequently Asked Questions (FAQ)
Q: What is the correct answer to 5 x 2 3 4 x 5?
A: There is no single "correct" answer without clarifying the intended operations. The expression is ambiguous. The answer depends on how the implicit operations are interpreted, as demonstrated by the various solutions presented above.
Q: Why is it important to use parentheses in mathematical expressions?
A: Parentheses remove ambiguity and ensure that the intended order of operations is followed consistently. This prevents errors and ensures that everyone understands the calculation correctly.
Q: Does the order of multiplication always matter?
A: In standard arithmetic, the order of multiplication doesn't affect the result (commutative property). However, in matrix multiplication, for example, the order does matter.
Conclusion: The Value of Precision in Mathematics
The analysis of the expression "5 x 2 3 4 x 5" provides a valuable lesson in the importance of precise mathematical notation. The ambiguity inherent in the expression highlights the crucial role of explicit operators and the consistent application of the order of operations. Without clear notation, different interpretations are possible, leading to varied results. Mastering the order of operations and employing unambiguous notation are essential skills for anyone working with mathematical expressions, regardless of their complexity. This understanding will serve you well whether you're tackling simple arithmetic problems or more complex mathematical equations. Always strive for clarity and precision in your mathematical work to avoid potential errors and misunderstandings. The seemingly simple expression serves as a powerful reminder of the importance of precise communication in mathematics.
Latest Posts
Latest Posts
-
How Does Odysseus Trick The Cyclops
Sep 07, 2025
-
What Is The Volume Of Water In A Graduated Cylinder
Sep 07, 2025
-
Which Of The Following Is True About Dna
Sep 07, 2025
-
Angles That Form A Linear Pair Add Up To
Sep 07, 2025
-
The Si Base Unit Of Mass Is The
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 5 X 2 3 4x 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.