5 X 1/2 As A Fraction
faraar
Sep 10, 2025 · 5 min read
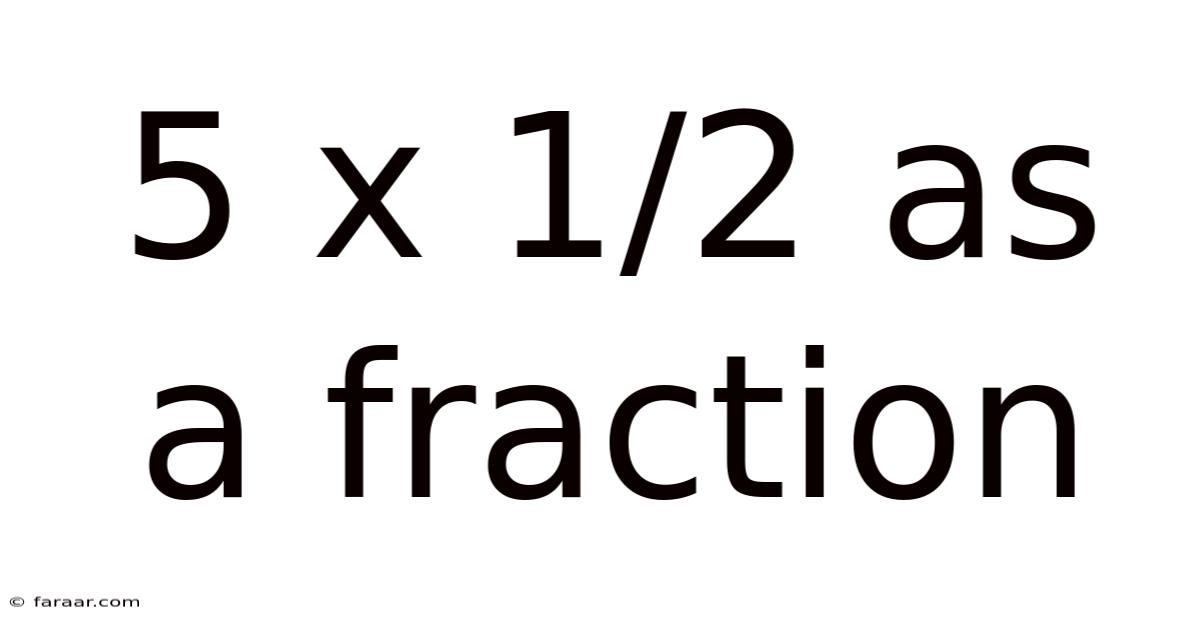
Table of Contents
5 x 1/2 as a Fraction: A Comprehensive Guide
Understanding fractions is a fundamental building block in mathematics. This article will delve into the seemingly simple problem of calculating 5 x 1/2 as a fraction, but in doing so, we'll explore the underlying principles of fraction multiplication, provide multiple approaches to solving the problem, and extend the understanding to more complex scenarios. By the end, you’ll not only know the answer but also possess a deeper understanding of how fractions work, empowering you to tackle similar problems with confidence.
Understanding the Basics: Fractions and Multiplication
Before diving into the calculation of 5 x 1/2, let's review the fundamentals. A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator is 1 and the denominator is 2. This represents one out of two equal parts. Multiplying fractions involves multiplying the numerators together and the denominators together.
Method 1: Direct Multiplication
The most straightforward approach to solving 5 x 1/2 is to treat the whole number 5 as a fraction itself. Any whole number can be expressed as a fraction by placing it over 1. Therefore, 5 can be written as 5/1.
Now, our problem becomes: (5/1) x (1/2)
Following the rule for multiplying fractions, we multiply the numerators: 5 x 1 = 5
And we multiply the denominators: 1 x 2 = 2
This gives us the resulting fraction: 5/2
Therefore, 5 x 1/2 = 5/2
This fraction, 5/2, is an improper fraction because the numerator (5) is larger than the denominator (2).
Method 2: Repeated Addition
Another way to visualize 5 x 1/2 is to consider it as repeated addition. We are essentially adding 1/2 to itself five times:
1/2 + 1/2 + 1/2 + 1/2 + 1/2
Since the denominators are the same, we can simply add the numerators: 1 + 1 + 1 + 1 + 1 = 5
Keeping the denominator the same, we get: 5/2
This method reinforces the concept that multiplication is repeated addition. It's a helpful approach for understanding the underlying meaning of the calculation, especially for those who are still developing their understanding of fraction multiplication.
Converting to Mixed Number
The improper fraction 5/2 is perfectly valid, but it's often more convenient to express it as a mixed number. A mixed number combines a whole number and a fraction. To convert 5/2 to a mixed number, we perform division:
5 ÷ 2 = 2 with a remainder of 1
The quotient (2) becomes the whole number part, and the remainder (1) becomes the numerator of the fraction. The denominator remains the same (2). Therefore, 5/2 as a mixed number is 2 1/2.
So, 5 x 1/2 = 5/2 = 2 1/2
Method 3: Visual Representation
Visualizing the problem can be extremely helpful, especially for beginners. Imagine a pizza cut into two equal slices (representing the denominator of 1/2). We want to find the total amount of pizza if we have five of those half-slices.
If you draw five half-pizzas, you'll see that you have 2 whole pizzas and one half-pizza remaining. This visually confirms that 5 x 1/2 = 2 1/2. This visual approach makes the concept more tangible and easier to grasp.
Extending the Understanding: Multiplying Fractions with Larger Numbers
The principles discussed above apply equally to multiplying fractions with larger numbers. Let's consider a more complex example:
7 x 3/4
First, we express 7 as a fraction: 7/1
Then, we multiply the fractions: (7/1) x (3/4) = (7 x 3) / (1 x 4) = 21/4
This improper fraction can be converted to a mixed number:
21 ÷ 4 = 5 with a remainder of 1
Therefore, 21/4 = 5 1/4. So, 7 x 3/4 = 5 1/4.
Simplifying Fractions
After multiplying fractions, it's often necessary to simplify the resulting fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. For example:
12/18
The GCD of 12 and 18 is 6. Dividing both numerator and denominator by 6 gives:
12/6 = 2 and 18/6 = 3
Therefore, 12/18 simplifies to 2/3. Always simplify your fractions to their simplest form for clarity and accuracy.
Frequently Asked Questions (FAQ)
Q: Why do we multiply the numerators and denominators separately?
A: This stems from the definition of multiplication. When you multiply fractions, you're essentially finding a portion of a portion. Multiplying the numerators gives you the total number of parts you have, while multiplying the denominators gives you the total number of parts the whole is divided into.
Q: What if I have a whole number multiplied by a mixed number?
A: First, convert the mixed number to an improper fraction. Then, treat the whole number as a fraction over 1 and multiply as usual. For example:
3 x 2 1/2 = 3 x (5/2) = 15/2 = 7 1/2
Q: Can I always convert an improper fraction to a mixed number?
A: Yes, you can always convert an improper fraction to a mixed number. It often makes the result easier to understand and visualize.
Q: Is there a way to avoid improper fractions entirely?
A: While you can sometimes perform the calculation in a way that avoids improper fractions initially, they are a natural part of fraction multiplication and often simplify the process. Understanding how to work with improper fractions is crucial.
Conclusion
Mastering fraction multiplication is a cornerstone of mathematical proficiency. While the calculation of 5 x 1/2 might seem simple at first glance, it provides a solid foundation for understanding more complex fractional operations. By understanding the various methods – direct multiplication, repeated addition, visual representation, and conversion to mixed numbers – you gain a deeper and more versatile understanding of fraction manipulation. Remember to always simplify your answers to their lowest terms for clarity and accuracy. With consistent practice and a grasp of the underlying principles, you'll become confident and proficient in handling any fraction-related problem.
Latest Posts
Latest Posts
-
Do You Have To Indent Dialogue
Sep 10, 2025
-
Write 35 As A Fraction In Simplest Form
Sep 10, 2025
-
A Student Needs To Prepare 250 Ml Of A
Sep 10, 2025
-
How To Find The Sum Of An Alternating Series
Sep 10, 2025
-
How Much Is 1 3 Pound
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5 X 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.