5 Of 20 Is What Percent
faraar
Sep 08, 2025 · 5 min read
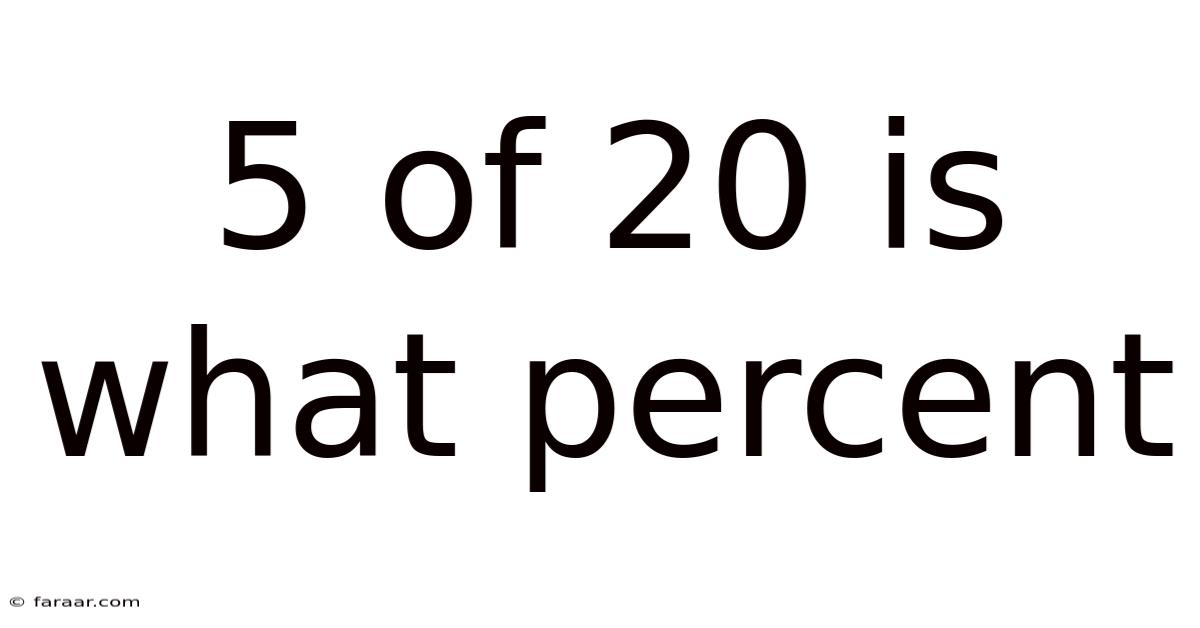
Table of Contents
5 out of 20 is What Percent? Understanding Percentages and Their Applications
Knowing how to calculate percentages is a fundamental skill in many aspects of life, from understanding sales discounts and calculating grades to comprehending financial statements and interpreting statistical data. This article will thoroughly explore how to determine what percentage 5 out of 20 represents, and then delve deeper into the underlying concepts and practical applications of percentage calculations. We'll cover the basics, explore different calculation methods, and provide examples to solidify your understanding. By the end, you'll not only know the answer to "5 out of 20 is what percent?" but you'll also have a strong grasp of percentages and their widespread utility.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 25%, for example, means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this fundamental relationship is key to calculating percentages.
Calculating "5 out of 20 is What Percent?"
The question "5 out of 20 is what percent?" can be solved using several methods. Let's explore the most common and straightforward approaches:
Method 1: Using the Fraction Method
This method involves expressing the given numbers as a fraction and then converting that fraction to a percentage.
-
Form a fraction: The phrase "5 out of 20" directly translates to the fraction 5/20.
-
Simplify the fraction (optional): To simplify the fraction, find the greatest common divisor (GCD) of the numerator (5) and the denominator (20). The GCD of 5 and 20 is 5. Divide both the numerator and the denominator by 5: 5/20 = 1/4. Simplifying makes the next step easier.
-
Convert the fraction to a decimal: Divide the numerator by the denominator: 1 ÷ 4 = 0.25
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percent sign (%): 0.25 × 100 = 25%.
Therefore, 5 out of 20 is 25%.
Method 2: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion to find the unknown percentage:
- Let x be the unknown percentage.
- We know that 5 out of 20 is equivalent to x out of 100.
This can be expressed as the proportion: 5/20 = x/100
To solve for x, we can cross-multiply:
20x = 500
Now, divide both sides by 20:
x = 500/20 = 25
Therefore, x = 25%, confirming that 5 out of 20 is 25%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 5 by 20 (5 ÷ 20 = 0.25) and then multiply the result by 100 (0.25 × 100 = 25). The calculator will automatically give you the answer as 25%.
Beyond the Basics: A Deeper Dive into Percentages
Understanding how to calculate percentages is just the beginning. Let's explore some more advanced concepts and their practical applications:
1. Percentage Increase and Decrease:
Percentages are frequently used to represent increases or decreases in values. For instance, if a product's price increases from $100 to $120, the percentage increase is calculated as follows:
- Find the difference: $120 - $100 = $20
- Divide the difference by the original value: $20 / $100 = 0.2
- Multiply by 100 to express as a percentage: 0.2 × 100 = 20%
Therefore, the price increased by 20%. Similar calculations can be done for percentage decreases.
2. Percentage Change:
Percentage change is a versatile tool used to compare values over time or across different categories. The formula is:
[(New Value - Old Value) / Old Value] × 100%
A positive result indicates an increase, while a negative result indicates a decrease. This is crucial for analyzing trends in various fields, such as finance, economics, and demographics.
3. Percentage Points:
It's important to distinguish between percentage points and percentages. If something increases from 20% to 30%, the increase is 10 percentage points, not 10%. The percentage increase is actually 50% [(30-20)/20 * 100%]. Understanding this distinction avoids misinterpretations.
4. Applications of Percentages in Real Life:
Percentages are ubiquitous in everyday life. Here are just a few examples:
- Sales and discounts: Stores frequently advertise discounts as percentages (e.g., 20% off).
- Grades and scores: Academic performance is often expressed as percentages.
- Taxes: Sales tax, income tax, and other taxes are calculated as percentages.
- Interest rates: Interest earned on savings accounts or paid on loans is expressed as a percentage.
- Statistics and data analysis: Percentages are essential for summarizing and interpreting data.
- Financial statements: Financial reports heavily rely on percentages to represent ratios and trends.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage of a number?
To calculate a percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to find 20% of 50, multiply 50 by 0.20 (50 × 0.20 = 10).
Q2: What is the difference between a percentage and a proportion?
A proportion is a ratio that compares two quantities. A percentage is a specific type of proportion where the second quantity is always 100. In essence, a percentage is a way of expressing a proportion out of 100.
Q3: How can I improve my understanding of percentages?
Practice is key! Try solving various percentage problems using different methods. You can find plenty of practice exercises online or in textbooks. Start with simpler problems and gradually increase the difficulty. Understanding the underlying concepts (fractions, decimals, proportions) is also crucial.
Q4: Are there any online tools or calculators to help with percentage calculations?
Yes, many online calculators and tools are available to assist with percentage calculations. These can be helpful for quick calculations or for verifying your own work.
Conclusion
In conclusion, 5 out of 20 is equal to 25%. This article has not only answered the initial question but also provided a comprehensive understanding of percentages, various methods for calculation, and their diverse applications in real-world scenarios. Mastering percentage calculations is a valuable skill that enhances your ability to interpret data, analyze information, and make informed decisions across many aspects of life and work. Remember that consistent practice and a firm grasp of the fundamental concepts will solidify your understanding and make you more confident in tackling percentage-related problems in the future.
Latest Posts
Latest Posts
-
How Many Atoms Are In A Body Centered Unit Cell
Sep 08, 2025
-
Verify That F And G Are Inverse Functions Algebraically
Sep 08, 2025
-
Does A Triangle Have Perpendicular Sides
Sep 08, 2025
-
Left Handed Guitar Lessons Near Me
Sep 08, 2025
-
Is The Experimental Group The Independent Variable
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 5 Of 20 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.