5 Less Than 3.1 Times A Number N
faraar
Sep 10, 2025 · 5 min read
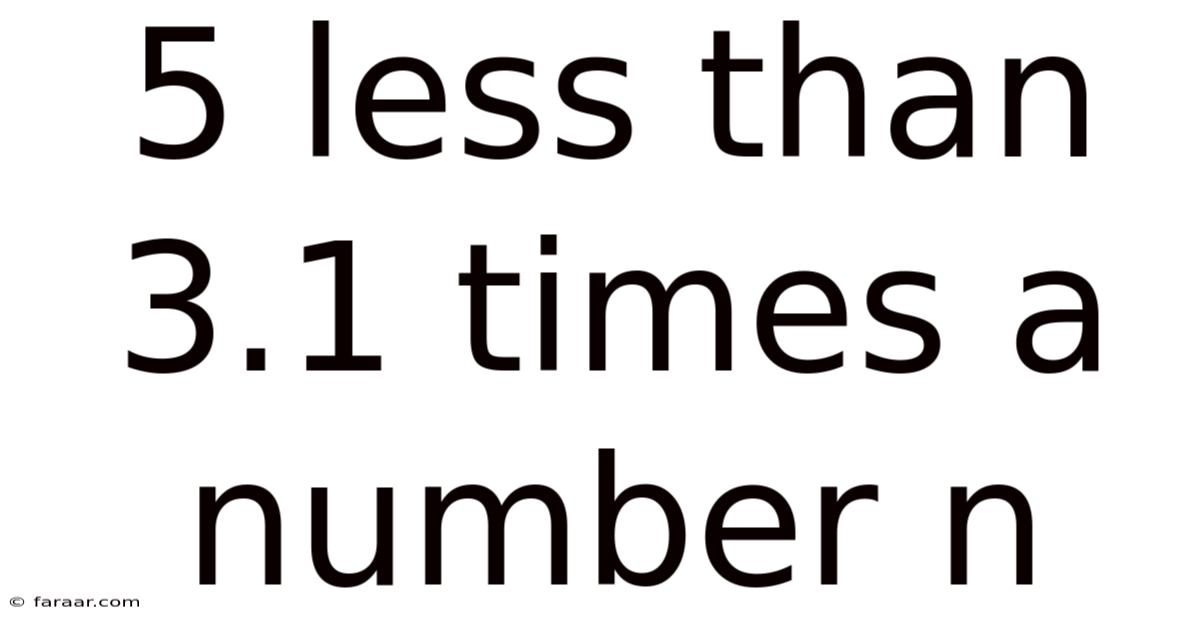
Table of Contents
Decoding "5 Less Than 3.1 Times a Number n": A Deep Dive into Algebraic Expressions
Understanding algebraic expressions is fundamental to success in mathematics and beyond. This article delves into the seemingly simple phrase "5 less than 3.1 times a number n," breaking down its meaning, exploring its practical applications, and tackling potential difficulties students might encounter. We will cover everything from translating the phrase into an algebraic equation to solving equations involving this expression and even exploring its relevance in real-world scenarios. By the end, you'll not only understand this specific expression but also gain a stronger grasp of algebraic concepts in general.
Introduction: Translating Words into Math
The phrase "5 less than 3.1 times a number n" is a verbal description of an algebraic expression. The key to understanding it lies in translating the words into mathematical symbols. Let's break it down step-by-step:
-
"a number n": This simply represents an unknown value, which we denote as the variable n.
-
"3.1 times a number n": This translates to 3.1 * n, or more concisely, 3.1n. This represents the multiplication of 3.1 and the variable n.
-
"5 less than 3.1 times a number n": This means we are subtracting 5 from the result of 3.1n. Therefore, the complete algebraic expression is 3.1n - 5.
This seemingly simple expression forms the basis for many mathematical problems. Understanding its construction is crucial for solving equations and tackling more complex algebraic concepts.
Understanding the Components: Variables and Coefficients
Let's examine the components of the expression 3.1n - 5:
-
Variable (n): A variable is a symbol (usually a letter) that represents an unknown quantity. In this case, n represents the unknown number. The value of n can change, making it a variable.
-
Coefficient (3.1): A coefficient is the numerical factor of a variable. Here, 3.1 is the coefficient of n. It indicates that the variable n is multiplied by 3.1.
-
Constant (-5): A constant is a term that has a fixed numerical value and does not contain any variables. In our expression, -5 is the constant term.
Understanding these components is essential to working with algebraic expressions. They allow us to manipulate and solve equations effectively.
Constructing and Solving Equations
The expression 3.1n - 5 can be part of a larger equation. For example, we might have an equation like:
3.1n - 5 = 10.3
To solve for n, we need to isolate the variable using algebraic techniques:
-
Add 5 to both sides: This cancels out the -5 on the left side, resulting in:
3.1n = 15.3
-
Divide both sides by 3.1: This isolates n:
n = 15.3 / 3.1 = 4.93548... (approximately 4.94)
Therefore, the solution to the equation 3.1n - 5 = 10.3 is approximately n = 4.94. Remember that depending on the context, you may need to round your answer to a specific number of decimal places.
Practical Applications: Real-World Scenarios
This seemingly simple algebraic expression has several real-world applications. Let's explore a few examples:
-
Calculating Earnings: Imagine you earn $3.10 per item sold, and you have fixed expenses of $5.00. The expression 3.1n - 5 would represent your profit (n being the number of items sold). If you sold 10 items, your profit would be 3.1(10) - 5 = $26.00.
-
Calculating Distance: Suppose you travel at an average speed of 3.1 miles per hour and you start 5 miles from your destination. The expression 3.1n - 5 could represent your distance from your destination after n hours of travel.
-
Analyzing Costs: In business, many cost calculations involve a fixed cost and a variable cost per unit. This expression could model the total cost, where the fixed cost is represented by -5 and the variable cost is represented by 3.1n (where n is the number of units).
These examples illustrate the practical relevance of algebraic expressions in various situations. Understanding how to translate real-world problems into mathematical expressions is a key skill in many fields.
Addressing Potential Challenges: Common Mistakes
Students often encounter difficulties when working with algebraic expressions like this. Here are some common pitfalls and how to avoid them:
-
Order of Operations: Remember the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). Failing to follow this order can lead to incorrect calculations.
-
Negative Numbers: Make sure you understand how to work with negative numbers, particularly in subtraction. Subtracting a negative number is equivalent to adding a positive number.
-
Decimal Arithmetic: Be careful when performing arithmetic with decimals. Use a calculator if necessary, but ensure you understand the steps involved.
-
Variable Misinterpretation: Clearly identify the variable and its meaning within the problem context.
Frequently Asked Questions (FAQ)
-
Q: What if the phrase was "5 less than n times 3.1"? A: This would translate to n(3.1) - 5, or equivalently, 3.1n - 5 – the same expression. The order of multiplication doesn't change the result.
-
Q: Can the number 3.1 be a different value? A: Absolutely! The expression can be generalized to "5 less than a times a number n", which translates to an - 5, where a represents any number.
-
Q: How do I solve equations involving more complex expressions including 3.1n - 5? A: You'll use the same principles of algebra: isolate the variable (n) by applying inverse operations (addition, subtraction, multiplication, division) to both sides of the equation. The complexity increases with the number of terms and operations, but the fundamental principles remain the same.
-
Q: Are there other ways to write this expression? A: While 3.1n - 5 is the most straightforward and commonly used form, it's mathematically equivalent to -5 + 3.1n. The order of the constant and variable term doesn't affect the result.
Conclusion: Mastering Algebraic Expressions
The seemingly simple phrase "5 less than 3.1 times a number n" encapsulates fundamental algebraic concepts. By understanding the translation of words into mathematical symbols, identifying the components of an algebraic expression (variable, coefficient, constant), and applying appropriate algebraic techniques, you can solve equations and tackle more complex problems. Remember to practice regularly, pay attention to the order of operations, and address any misconceptions about negative numbers and decimals. The ability to work confidently with algebraic expressions is a cornerstone of mathematical proficiency, opening doors to more advanced concepts and applications in various fields. Mastering this fundamental skill will undoubtedly benefit you in your future mathematical endeavors.
Latest Posts
Latest Posts
-
Each Pair Of Figures Is Similar Find The Missing Side
Sep 10, 2025
-
The Population Of A Town Increased From 7800 To 8775
Sep 10, 2025
-
What Is The Molar Mass Of Aspirin
Sep 10, 2025
-
How To Say Weeks In Spanish
Sep 10, 2025
-
How Many 1 3 Cups Equal 2 3 Cups
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5 Less Than 3.1 Times A Number N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.