5/9 + 5/9 As A Fraction
faraar
Sep 23, 2025 · 6 min read
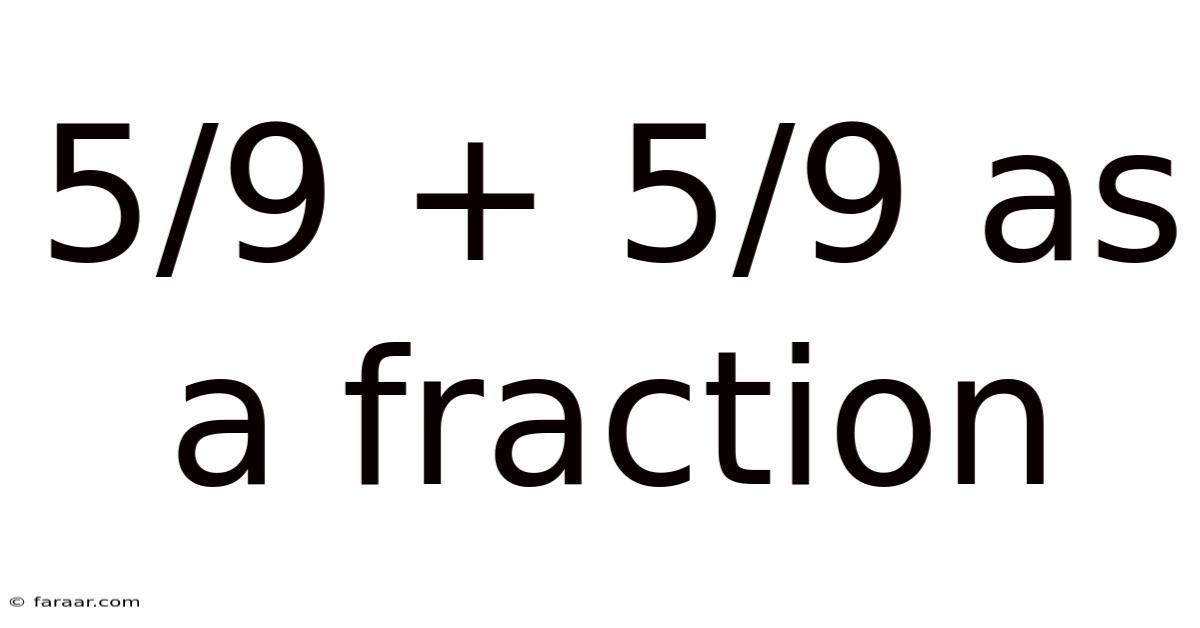
Table of Contents
Mastering Fractions: A Deep Dive into 5/9 + 5/9
Adding fractions might seem simple at first glance, but a thorough understanding of the underlying principles is crucial for mastering more complex mathematical concepts. This comprehensive guide will walk you through the process of adding 5/9 + 5/9, not just providing the answer but also exploring the fundamental concepts of fractions and demonstrating various approaches to solve similar problems. This will equip you with the skills to confidently tackle fraction addition in any context.
Understanding Fractions: Building Blocks of Arithmetic
Before diving into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 5/9, 9 represents the total number of equal parts, and 5 represents the number of parts we're interested in.
Adding Fractions with the Same Denominator: A Simple Approach
The beauty of adding fractions with the same denominator, like 5/9 and 5/9, lies in its simplicity. When the denominators are identical, we simply add the numerators and keep the denominator unchanged. This is because we're dealing with the same-sized parts of the whole.
Let's apply this to our problem: 5/9 + 5/9
- Add the numerators: 5 + 5 = 10
- Keep the denominator the same: The denominator remains 9.
Therefore, 5/9 + 5/9 = 10/9
This is an improper fraction because the numerator (10) is larger than the denominator (9).
Converting Improper Fractions to Mixed Numbers
Improper fractions are perfectly valid, but they are often expressed as mixed numbers for better understanding and readability. A mixed number combines a whole number and a proper fraction. To convert 10/9 to a mixed number:
- Divide the numerator by the denominator: 10 ÷ 9 = 1 with a remainder of 1.
- The quotient becomes the whole number: The quotient 1 is the whole number part of the mixed number.
- The remainder becomes the numerator of the proper fraction: The remainder 1 becomes the numerator.
- The denominator remains the same: The denominator remains 9.
Therefore, 10/9 is equivalent to 1 1/9.
Visualizing Fraction Addition: A Concrete Approach
Imagine you have two pizzas, each cut into 9 equal slices. In the first pizza, you eat 5 slices (5/9). In the second pizza, you eat another 5 slices (5/9). In total, you've eaten 10 slices (10/9) out of a possible 18 slices (considering both pizzas as a whole). This visually demonstrates that 5/9 + 5/9 = 10/9 or 1 1/9. This visual representation makes the concept more intuitive and easier to grasp, especially for beginners.
Adding Fractions with Different Denominators: A More Challenging Scenario
While our example dealt with fractions sharing the same denominator, let's briefly touch upon adding fractions with different denominators. This requires finding a common denominator, which is a multiple of both denominators. Once you have a common denominator, you convert each fraction to an equivalent fraction with that denominator and then add the numerators.
For instance, let's add 1/2 + 1/3.
- Find the least common multiple (LCM) of the denominators: The LCM of 2 and 3 is 6.
- Convert each fraction to an equivalent fraction with the common denominator:
- 1/2 = 3/6 (multiply numerator and denominator by 3)
- 1/3 = 2/6 (multiply numerator and denominator by 2)
- Add the numerators: 3/6 + 2/6 = 5/6
Therefore, 1/2 + 1/3 = 5/6
Practical Applications of Fraction Addition
Understanding fraction addition is not just an academic exercise; it has numerous real-world applications. Consider the following examples:
- Baking: Recipes often call for fractional amounts of ingredients. Adding fractions helps determine the total amount needed.
- Construction: Measurements in construction frequently involve fractions of inches or feet. Adding fractions is essential for accurate calculations.
- Finance: Working with budgets and calculating portions of a whole often involves fraction addition.
- Data analysis: Many statistical calculations rely on fractions and their addition for meaningful interpretations.
Simplifying Fractions: Reducing to Lowest Terms
After adding fractions, it's often necessary to simplify the result to its lowest terms. This means reducing the fraction to its simplest form where the numerator and denominator have no common factors other than 1. For instance, 10/9 is already in its simplest form (as an improper fraction), but 1 1/9 is similarly simplified as a mixed number.
To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator and divide both by the GCD. For example, let's simplify 6/12:
- Find the GCD of 6 and 12: The GCD is 6.
- Divide both numerator and denominator by the GCD: 6 ÷ 6 = 1 and 12 ÷ 6 = 2.
- The simplified fraction is: 1/2
Frequently Asked Questions (FAQ)
Q: What if I have more than two fractions to add?
A: Follow the same principles. If the denominators are the same, add the numerators. If the denominators are different, find a common denominator before adding.
Q: Can I add fractions and whole numbers together?
A: Yes, convert the whole number into a fraction with the same denominator as the fraction you are adding it to. For example, to add 2 + 1/3, convert 2 to 6/3, then add 6/3 + 1/3 = 7/3 or 2 1/3
Q: What if I get a negative fraction?
A: Negative fractions are handled the same way as positive fractions, but remember to keep track of the signs. The rules for adding integers apply (adding two negative numbers results in a negative number; adding a positive and a negative number involves subtracting the smaller absolute value from the larger and keeping the sign of the larger).
Q: Are there any online tools or calculators to help with fraction addition?
A: Yes, many online calculators and resources can assist with fraction addition. These tools can be particularly helpful for more complex fraction problems. However, understanding the underlying principles remains vital for effective problem-solving.
Conclusion: Mastering Fractions—A Stepping Stone to Success
Adding 5/9 + 5/9, resulting in 10/9 or 1 1/9, is more than just a simple arithmetic problem; it's a stepping stone toward a deeper understanding of fractions and their applications. By grasping the fundamental principles of adding fractions—whether they have the same denominator or not—you build a solid foundation for tackling more advanced mathematical concepts. Remember to visualize the process, practice regularly, and explore different approaches to solidify your understanding. This mastery will not only improve your mathematical skills but also enhance your problem-solving abilities in various aspects of life. The ability to manipulate fractions confidently will undoubtedly serve you well throughout your academic journey and beyond.
Latest Posts
Latest Posts
-
Find A Unit Vector That Is Orthogonal To Both And
Sep 23, 2025
-
How Do I Figure Out What To Major In
Sep 23, 2025
-
What Is The Sum Of 4 And 4
Sep 23, 2025
-
How To Find Ph At The Equivalence Point
Sep 23, 2025
-
The Quotient Of C And 8
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5/9 + 5/9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.