5 - 5 X 5 + 5
faraar
Sep 01, 2025 · 5 min read
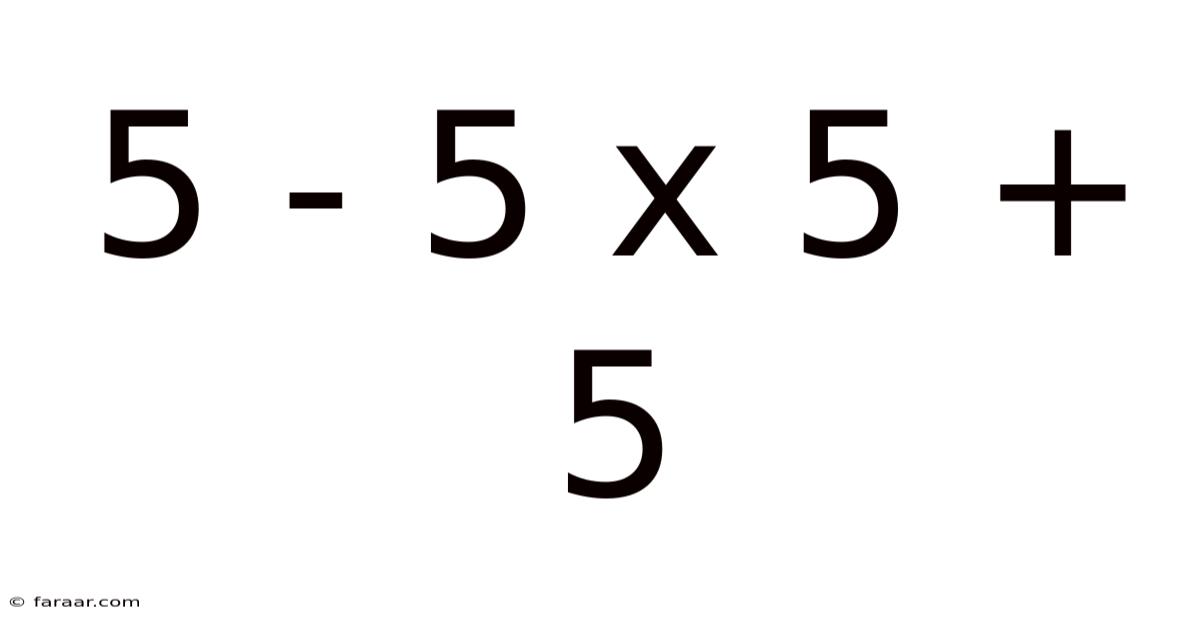
Table of Contents
Unraveling the Mystery: A Deep Dive into 5 - 5 x 5 + 5
This seemingly simple mathematical expression, 5 - 5 x 5 + 5, often trips up even those comfortable with basic arithmetic. The key to solving it lies not in complex formulas, but in understanding the fundamental order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). This article will not only provide the solution but also explore the underlying principles, common mistakes, and the broader significance of order of operations in mathematics. We’ll also delve into practical applications and frequently asked questions surrounding this seemingly simple equation.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before we tackle our equation, let's solidify our understanding of PEMDAS (or BODMAS, which stands for Brackets, Orders, Division and Multiplication, Addition and Subtraction). This mnemonic device dictates the sequence in which mathematical operations should be performed:
-
Parentheses/Brackets: Calculations within parentheses or brackets are always performed first. This ensures that any grouped operations are completed before moving to the rest of the equation.
-
Exponents/Orders: Exponents (or orders, representing powers and roots) are evaluated next. This means any numbers raised to a power are calculated before other operations.
-
Multiplication and Division: Multiplication and division have equal precedence. If an equation contains both, they are performed from left to right.
-
Addition and Subtraction: Similarly, addition and subtraction have equal precedence and are performed from left to right if both appear in the equation.
Solving 5 - 5 x 5 + 5 Step-by-Step
Now, let's apply PEMDAS to solve 5 - 5 x 5 + 5:
-
Multiplication: The first operation according to PEMDAS is multiplication. Therefore, we calculate 5 x 5 = 25. Our equation now becomes: 5 - 25 + 5
-
Addition and Subtraction: Next, we perform addition and subtraction from left to right. First, 5 - 25 = -20. Then, -20 + 5 = -15.
Therefore, the solution to 5 - 5 x 5 + 5 is -15.
Common Mistakes and Misinterpretations
A frequent mistake is performing the operations from left to right without considering the order of operations. This would lead to an incorrect answer:
5 - 5 = 0; 0 x 5 = 0; 0 + 5 = 5. This is wrong!
This highlights the critical importance of adhering to PEMDAS. Ignoring the order of operations can lead to significantly different, and incorrect, results.
The Importance of Order of Operations in Real-World Applications
The order of operations isn't just an abstract mathematical concept; it's fundamental to numerous real-world applications. Consider these examples:
-
Programming: Computer programming languages strictly adhere to the order of operations. Incorrectly ordering operations in a program can lead to bugs and unexpected results. Understanding PEMDAS is essential for writing accurate and functional code.
-
Engineering and Physics: Engineering and physics calculations frequently involve multiple operations. The correct application of the order of operations is crucial for accurate calculations in areas such as structural design, circuit analysis, and trajectory prediction.
-
Finance and Accounting: Financial calculations, such as compound interest calculations, rely on the order of operations to accurately determine returns and balances. Mistakes in these calculations can have significant financial repercussions.
-
Everyday Calculations: Even in everyday situations, understanding order of operations can prevent errors. Consider a scenario where you're calculating the total cost of items after applying discounts and taxes. The order in which these operations are performed will directly impact the final result.
Expanding the Understanding: Beyond Basic Arithmetic
While the equation 5 - 5 x 5 + 5 demonstrates a basic application of PEMDAS, the principles extend to more complex mathematical expressions involving parentheses, exponents, and other operations. Let's explore a slightly more complex example:
(10 + 5) / 5 - 2^2 + 3 x 2
-
Parentheses: First, we solve the expression inside the parentheses: 10 + 5 = 15. The equation becomes: 15 / 5 - 2^2 + 3 x 2
-
Exponents: Next, we calculate the exponent: 2^2 = 4. The equation becomes: 15 / 5 - 4 + 3 x 2
-
Multiplication and Division (from left to right): First, 15 / 5 = 3. Then, 3 x 2 = 6. The equation is now: 3 - 4 + 6
-
Addition and Subtraction (from left to right): 3 - 4 = -1; -1 + 6 = 5
The solution to (10 + 5) / 5 - 2^2 + 3 x 2 is 5.
This example shows how PEMDAS extends beyond simple addition, subtraction, multiplication, and division to include more advanced operations. Consistent application of the order of operations remains crucial for accurate calculations.
Frequently Asked Questions (FAQ)
Q: What happens if there are multiple operations with the same precedence in an equation?
A: If an equation contains multiple operations with the same precedence (e.g., multiple multiplications or divisions), they are performed from left to right.
Q: Can I use a calculator to solve equations like this?
A: Most scientific calculators are programmed to follow the order of operations automatically. However, it's still crucial to understand PEMDAS to ensure you are interpreting the results correctly and to avoid potential errors from improperly entering the equation into the calculator. Simple calculators may not correctly interpret the order of operations, leading to incorrect results.
Q: Are there any exceptions to PEMDAS?
A: While PEMDAS is a widely accepted standard, context is always key. In certain specialized mathematical notations or contexts, there might be variations or additions to the standard order. However, for the vast majority of general mathematical expressions, PEMDAS provides the correct approach.
Q: Why is it so important to learn PEMDAS?
A: Mastering PEMDAS is essential for accurate and reliable mathematical calculations. It's a fundamental concept that underpins more advanced mathematical concepts and has practical applications across various fields. Understanding and applying it correctly prevents errors and ensures consistency in results.
Conclusion: Mastering the Order of Operations
The seemingly simple equation 5 - 5 x 5 + 5 serves as a potent reminder of the crucial role of the order of operations in mathematics. While the solution (-15) might seem straightforward once the principles of PEMDAS are applied, the frequent mistakes made highlight the importance of understanding and adhering to this fundamental mathematical rule. By mastering PEMDAS, we not only solve equations accurately but also develop a deeper understanding of the structure and logic that underpin mathematical calculations, proving invaluable across various disciplines and real-world scenarios. Remember, it's not just about getting the right answer; it's about understanding why that answer is correct. This understanding builds a stronger foundation for more advanced mathematical concepts and problem-solving in the future.
Latest Posts
Latest Posts
-
How To Find The Length Of Angle Bisector
Sep 02, 2025
-
What Is The Tension In The Rope
Sep 02, 2025
-
What Percentage Is 8 Hours In A Day
Sep 02, 2025
-
7 6 Rounded To The Nearest Tenth
Sep 02, 2025
-
How Do You Write 1 12 As A Decimal
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about 5 - 5 X 5 + 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.