40 Of What Number Is 46
faraar
Aug 28, 2025 · 5 min read
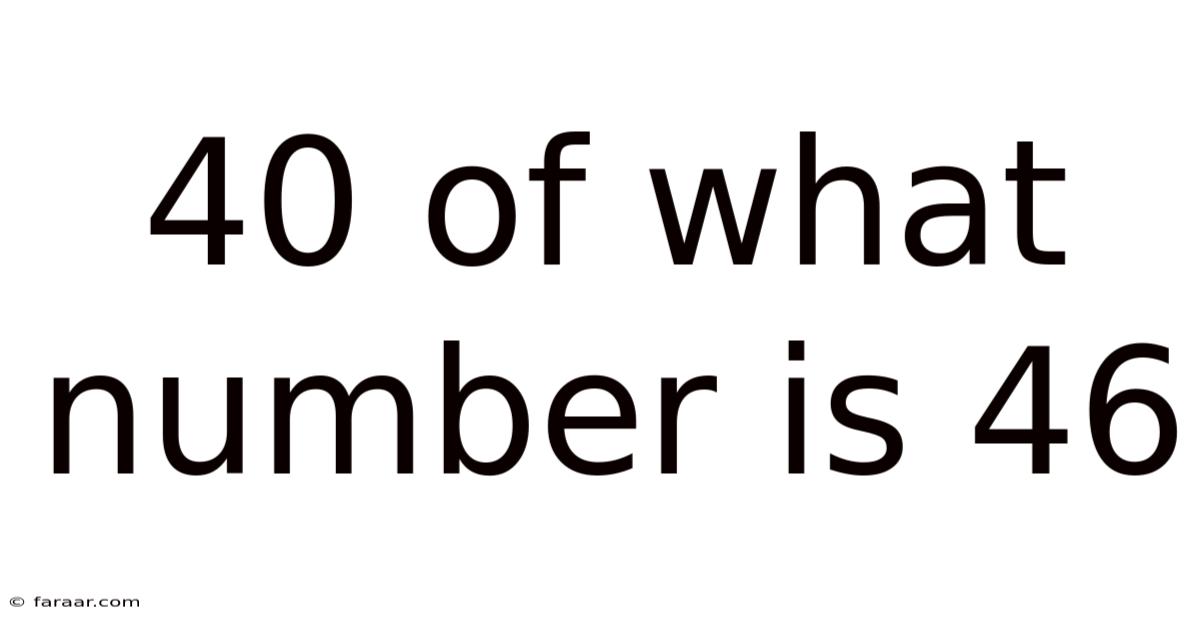
Table of Contents
Decoding the Mystery: 40% of What Number is 46? A Comprehensive Guide
This article unravels the solution to the mathematical problem: "40% of what number is 46?" We'll explore the problem-solving process step-by-step, providing a clear understanding of the underlying concepts of percentages, proportions, and algebraic equations. This guide caters to learners of all levels, from those just beginning to grasp percentages to those seeking a deeper understanding of mathematical problem-solving strategies. We'll cover multiple approaches, ensuring you'll grasp the core principles and confidently tackle similar problems in the future. This comprehensive explanation will cover not only the solution but also the broader mathematical context and practical applications.
Understanding the Problem: Percentages and Proportions
Before diving into the solution, let's solidify our understanding of the core concepts. The problem "40% of what number is 46?" essentially asks us to find an unknown number (let's call it 'x') such that 40% of that number equals 46. This problem involves two key mathematical ideas:
-
Percentages: A percentage is a way of expressing a number as a fraction of 100. For example, 40% can be written as 40/100, or its simplified form, 2/5. Percentages are extensively used to represent proportions, rates, and changes in various fields, from finance and statistics to everyday life.
-
Proportions: A proportion is a statement that two ratios are equal. In this problem, we have an implicit proportion: 40/100 = 46/x. This proportion equates the ratio of 40 to 100 (representing 40%) to the ratio of 46 to the unknown number x. Solving for x allows us to find the number that satisfies this proportion.
Method 1: Solving using Proportions
This method uses the direct relationship between percentages and proportions to solve the problem. We set up the proportion as follows:
40/100 = 46/x
To solve for x, we cross-multiply:
40 * x = 46 * 100
40x = 4600
Now, we isolate x by dividing both sides of the equation by 40:
x = 4600 / 40
x = 115
Therefore, 40% of 115 is 46.
Method 2: Solving using a Percentage Equation
This method uses the equation that directly represents the relationship between the percentage, the whole number, and the resulting part. We can express the problem as an equation:
0.40 * x = 46
Here, 0.40 represents 40% expressed as a decimal (40/100 = 0.40). To solve for x, we divide both sides of the equation by 0.40:
x = 46 / 0.40
x = 115
Again, we find that x = 115.
Method 3: Solving using the Unitary Method
The unitary method involves finding the value of one unit (in this case, 1%) and then scaling it up to find the value of the required percentage.
First, we find the value of 1% of the unknown number:
If 40% of x = 46, then
1% of x = 46 / 40
1% of x = 1.15
Now, to find the value of 100% (the whole number x), we multiply the value of 1% by 100:
x = 1.15 * 100
x = 115
Verifying the Solution
It's crucial to verify our solution to ensure accuracy. We can do this by substituting x = 115 back into the original problem:
40% of 115 = (40/100) * 115 = 0.40 * 115 = 46
This confirms that our solution, x = 115, is correct.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Retail: Determining sale prices, markups, and discounts.
- Statistics: Analyzing data, representing proportions, and understanding distributions.
- Science: Measuring concentrations, expressing experimental results, and analyzing data.
- Everyday Life: Calculating tips, comparing prices, and understanding proportions in recipes.
Expanding on Percentage Concepts: More Complex Problems
The problem "40% of what number is 46?" serves as a foundation for understanding more complex percentage problems. These might involve:
- Multiple percentages: For example, finding a number after successive percentage increases or decreases.
- Compound interest: Calculating interest that accumulates over time, including interest earned on previously earned interest.
- Percentage change: Determining the percentage increase or decrease between two values.
- Percentage points: Distinguishing between percentage change and percentage points, which are often confused.
Understanding the fundamental principles demonstrated in this article will provide a solid base for tackling these more advanced percentage calculations.
Frequently Asked Questions (FAQ)
Q1: What if the percentage is more than 100%?
A1: If the percentage is over 100%, it means the resulting value is greater than the original number. The same principles apply; you would simply solve the equation as before, and the answer will be greater than the known part. For example, "150% of what number is 75?" would lead to a smaller original number.
Q2: Can I use a calculator to solve percentage problems?
A2: Absolutely! Calculators are incredibly useful for solving percentage problems, especially when dealing with complex numbers or multiple calculations. Most calculators have a percentage function (%) that simplifies the process.
Q3: What if the problem involved a different percentage and a different resulting value?
A3: The same methods outlined above can be applied. Simply replace the given percentage and the resulting value in the equations or proportions, and follow the steps to solve for the unknown number.
Q4: Are there any other methods to solve percentage problems?
A4: Yes, depending on the complexity and specific context of the problem, other methods may be more efficient. These might include using ratios, algebraic manipulations, or spreadsheet software.
Conclusion: Mastering Percentage Calculations
This article has provided a thorough explanation of how to solve the problem "40% of what number is 46?", employing various methods to reinforce understanding. We've explored the fundamental concepts of percentages and proportions and shown how to apply them practically. Remember, the key to mastering percentage calculations lies in understanding the underlying principles and choosing the most appropriate method for each problem. By practicing these methods and tackling various problems, you'll build confidence and proficiency in solving percentage-related questions, empowering you to apply these skills effectively in various academic and real-world contexts. The ability to understand and calculate percentages is a crucial skill that extends far beyond basic mathematics and into many facets of everyday life.
Latest Posts
Latest Posts
-
Which Fraction Is Equal To 4 5
Aug 28, 2025
-
Ethos In The Declaration Of Independence
Aug 28, 2025
-
180 Degree Rotation About The Origin
Aug 28, 2025
-
How Many Cubes With Side Lengths Of 1 3
Aug 28, 2025
-
Spanish Tutors Near Me For Adults
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about 40 Of What Number Is 46 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.