4 5 Divided By 3 7
faraar
Sep 14, 2025 · 5 min read
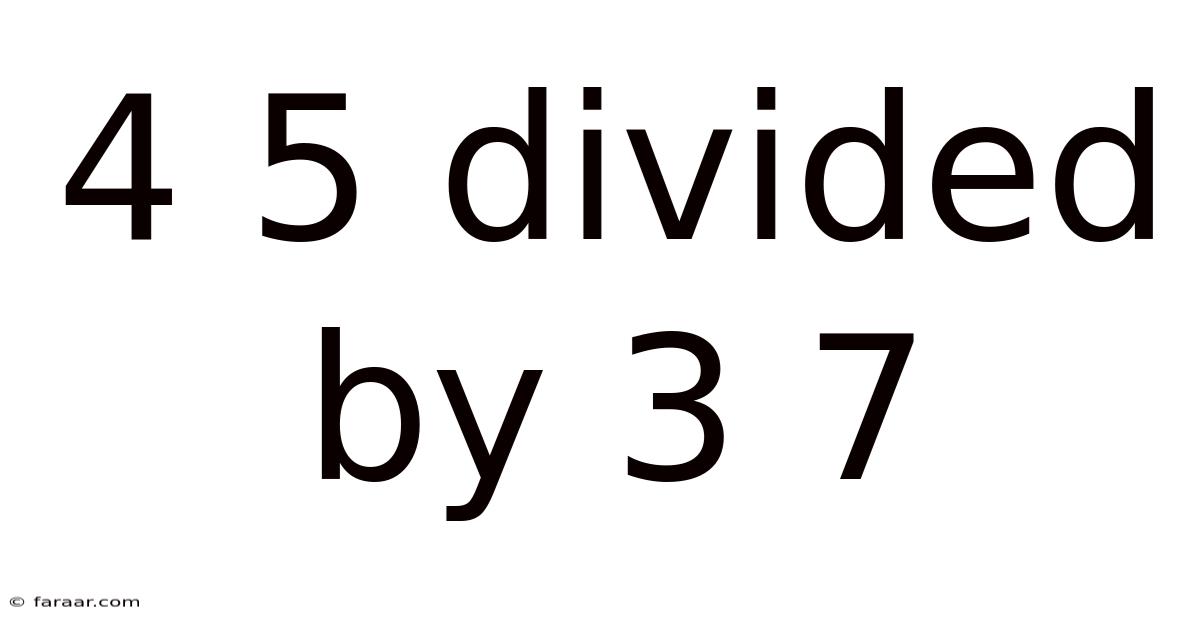
Table of Contents
Diving Deep into the Division: 45 ÷ 37
This article explores the division problem 45 ÷ 37, going beyond a simple answer to understand the underlying mathematical concepts and practical applications. We'll examine different methods of solving this problem, including long division, decimal representation, and the concept of remainders. This exploration is valuable not just for understanding basic arithmetic, but for building a stronger foundation in mathematics and problem-solving skills. We'll also delve into the related concepts of fractions, decimals, and the significance of remainders in various real-world contexts.
Understanding the Problem: 45 ÷ 37
At its core, 45 ÷ 37 asks: "How many times does 37 fit into 45?". This is a classic division problem where 45 is the dividend (the number being divided), and 37 is the divisor (the number dividing the dividend). The answer we're seeking is the quotient. Since 37 is larger than 45, we anticipate a quotient less than 1, with a remainder representing the portion of 45 that's left over after dividing by 37.
Method 1: Long Division
Long division is a systematic method for performing division, particularly useful when dealing with larger numbers. Let's work through 45 ÷ 37 using this method:
1
------
37 | 45
-37
---
8
- We start by seeing how many times 37 goes into 45. It goes in once (1 x 37 = 37).
- We subtract 37 from 45, resulting in 8. This 8 is the remainder.
Therefore, 45 ÷ 37 = 1 with a remainder of 8. This can be written as 1 R8.
Method 2: Decimal Representation
While the remainder provides a clear answer, we can also express the result as a decimal. To do this, we continue the long division process by adding a decimal point and zeros to the dividend:
1.216...
------
37 | 45.000
-37
---
80
-74
---
60
-37
---
230
-222
---
8
We can continue this process indefinitely, adding more zeros and performing the subtraction. However, this division produces a repeating decimal, approximately 1.216.
Method 3: Fractional Representation
Another way to represent the result is as a fraction. The remainder (8) becomes the numerator, and the divisor (37) becomes the denominator:
45 ÷ 37 = 1 + 8/37
This fraction, 8/37, represents the portion of 45 that doesn't divide evenly by 37. This fractional representation is particularly useful in certain mathematical contexts and provides a precise representation of the division's result.
Understanding Remainders
The remainder, in this case, 8, signifies the portion of the dividend (45) that is left over after the division. It’s a crucial part of the result and holds practical significance in various scenarios:
- Real-World Applications: Imagine you have 45 apples and want to distribute them equally among 37 people. Each person would receive one apple (the quotient), and you would have 8 apples left over (the remainder).
- Measurement and Conversions: When converting units, remainders can represent the excess amount. For example, converting 45 inches into feet (12 inches per foot) would result in 3 feet with a remainder of 9 inches.
- Computer Science: Remainders are fundamental in computer algorithms like modular arithmetic, used extensively in cryptography and data processing.
Exploring Related Concepts
The problem 45 ÷ 37 touches upon several key mathematical concepts:
- Divisibility: This explores the relationship between a dividend and a divisor and whether the division results in a whole number (no remainder) or a remainder. 45 is not divisible by 37.
- Factors and Multiples: Understanding factors and multiples helps us predict divisibility. Since 37 is a prime number (only divisible by 1 and itself), it's less likely to be a factor of most numbers.
- Prime Numbers and Composite Numbers: The divisor, 37, is a prime number, while 45 is a composite number (meaning it has factors other than 1 and itself). The interaction between prime and composite numbers affects the outcome of division.
- Rational and Irrational Numbers: The result, when expressed as a decimal (approximately 1.216...), is a rational number (it can be expressed as a fraction).
Frequently Asked Questions (FAQ)
-
Q: Why is the decimal representation of 45 ÷ 37 a repeating decimal?
- A: Because the fraction 8/37 cannot be simplified to a fraction with a denominator that is a power of 10. When the long division is performed, the remainder repeats, leading to a repeating decimal pattern.
-
Q: What if I round the decimal answer?
- A: Rounding introduces an approximation. While convenient for certain applications, it's essential to remember that the rounded value is not exactly equal to the true value of 45 ÷ 37.
-
Q: How is this division used in advanced mathematics?
- A: The principles underlying this division, including remainders and fractional representations, are crucial in fields like calculus, linear algebra, and number theory. Understanding the basics is a foundational step in more advanced mathematical studies.
-
Q: Are there other ways to solve this problem?
- A: While long division and calculator methods are common, other techniques, such as using algorithms or computer programming, can also be employed to solve division problems.
Conclusion: Beyond the Numbers
Solving 45 ÷ 37 is more than just performing a calculation; it's about understanding the underlying mathematical concepts. By exploring the different methods, understanding remainders, and connecting this problem to broader mathematical principles, we gain a deeper appreciation for the power and versatility of division. This understanding serves as a stepping stone for tackling more complex mathematical problems and applying mathematical thinking to various real-world situations. The seemingly simple problem of 45 ÷ 37 becomes a gateway to a wider understanding of numbers, their relationships, and their applications in diverse contexts. The journey from a simple division problem to a comprehensive understanding of related concepts highlights the beauty and depth of mathematics.
Latest Posts
Latest Posts
-
Does Mg Lose Or Gain Electrons
Sep 14, 2025
-
What Never Asks Questions But Answers
Sep 14, 2025
-
How To Calculate Upper And Lower Limits
Sep 14, 2025
-
Can An Object Have A Negative Acceleration While Speeding Up
Sep 14, 2025
-
How Long Would It Take To Drive 250 Miles
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4 5 Divided By 3 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.