4 1 2 X 4 1 2
faraar
Aug 27, 2025 · 6 min read
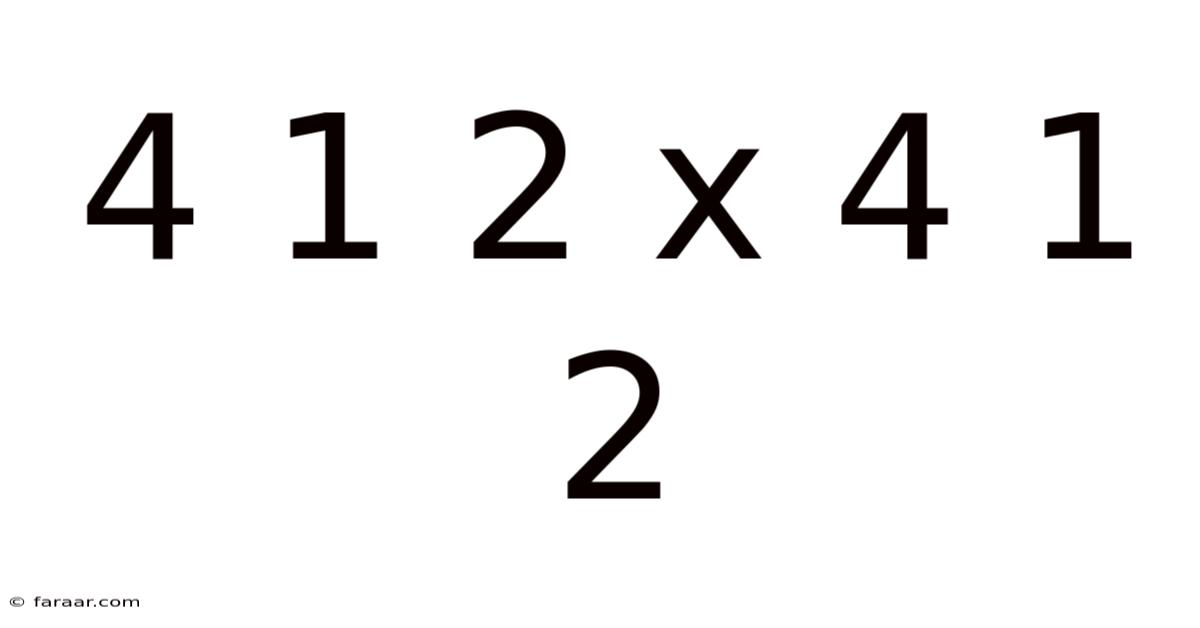
Table of Contents
Decoding 4 1/2 x 4 1/2: A Deep Dive into Fractions, Area, and Volume
This article explores the seemingly simple calculation of 4 1/2 x 4 1/2, expanding beyond the basic arithmetic to delve into its practical applications in geometry, particularly concerning area and volume calculations. We will cover the fundamental principles of fraction multiplication, demonstrate different methods of solving the problem, and discuss real-world scenarios where such calculations are crucial. This comprehensive guide is designed for students, educators, and anyone interested in gaining a deeper understanding of fractions and their relevance in everyday life.
I. Understanding the Fundamentals: Fractions and Multiplication
Before we tackle 4 1/2 x 4 1/2, let's solidify our understanding of fraction multiplication. A fraction, represented as a/b, signifies a part of a whole. The number 'a' is the numerator (the top number), representing the number of parts you have, and 'b' is the denominator (the bottom number), representing the total number of equal parts the whole is divided into.
Multiplying fractions is straightforward: you multiply the numerators together to get the new numerator, and you multiply the denominators together to get the new denominator. For example:
(a/b) x (c/d) = (a x c) / (b x d)
However, our problem involves mixed numbers – numbers that combine a whole number and a fraction (e.g., 4 1/2). To multiply mixed numbers, we must first convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: 4 x 2 = 8
- Add the numerator to the result: 8 + 1 = 9
- Keep the same denominator: 2
Therefore, 4 1/2 becomes 9/2.
II. Solving 4 1/2 x 4 1/2: Step-by-Step Calculation
Now, armed with this knowledge, let's solve 4 1/2 x 4 1/2:
-
Convert mixed numbers to improper fractions: 4 1/2 = 9/2. Our problem becomes (9/2) x (9/2).
-
Multiply the numerators: 9 x 9 = 81
-
Multiply the denominators: 2 x 2 = 4
-
Simplify the resulting improper fraction: We now have 81/4. To convert this back to a mixed number, divide the numerator by the denominator: 81 ÷ 4 = 20 with a remainder of 1.
-
Express the answer as a mixed number: The final answer is 20 1/4.
Therefore, 4 1/2 x 4 1/2 = 20 1/4.
III. Alternative Methods: Decimal Conversion
Another approach involves converting the mixed numbers to decimals before multiplying. 4 1/2 is equivalent to 4.5. Therefore, the calculation becomes 4.5 x 4.5. Using a calculator or manual multiplication:
4.5 x 4.5 = 20.25
Notice that 20.25 is the decimal equivalent of 20 1/4. Both methods yield the same result, demonstrating the interchangeability of fractions and decimals.
IV. Practical Applications: Area and Volume Calculations
The result of 4 1/2 x 4 1/2 finds significant practical application in geometry, specifically in calculating the area of squares and the volume of cubes.
-
Area of a Square: The area of a square is calculated by multiplying the length of one side by itself (side x side). If a square has sides of 4 1/2 units (e.g., feet, meters, inches), its area is (4 1/2) x (4 1/2) = 20.25 square units. This could represent the area of a room, a plot of land, or any square-shaped surface.
-
Volume of a Cube: The volume of a cube is calculated by multiplying the length of one side by itself three times (side x side x side). A cube with sides of 4 1/2 units would have a volume of (4 1/2) x (4 1/2) x (4 1/2) = (20.25) x 4.5 = 91.125 cubic units. This could represent the volume of a container, a box, or any cube-shaped object.
V. Expanding the Concept: Beyond Squares and Cubes
The principles of fraction multiplication and area/volume calculations extend far beyond simple squares and cubes. Consider these examples:
-
Rectangles: If a rectangle has dimensions of 4 1/2 units by 6 units, its area would be calculated as (4 1/2) x 6 = 27 square units. This is a direct application of the same principles.
-
Other Polygons: More complex shapes can be broken down into simpler shapes (squares, rectangles, triangles) whose areas can be individually calculated and then summed to find the total area.
-
Three-Dimensional Shapes: Similarly, more complex three-dimensional shapes can be broken down into simpler shapes (cubes, rectangular prisms, pyramids) to calculate the total volume.
VI. Error Analysis and Troubleshooting
When working with fractions, several common errors can occur:
-
Incorrect Conversion to Improper Fractions: Carefully follow the steps for converting mixed numbers to improper fractions. An incorrect conversion will lead to an incorrect final answer.
-
Errors in Multiplication: Double-check your multiplication of both the numerators and denominators. Using a calculator can help reduce the risk of simple arithmetic errors.
-
Failure to Simplify: Always simplify your final answer to its lowest terms. An improper fraction should be converted to a mixed number for easier interpretation.
VII. Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this directly? A: While you can convert the mixed numbers to decimals and use a calculator, understanding the underlying principles of fraction multiplication is crucial for more complex problems.
-
Q: What if the mixed numbers had different denominators? A: You would need to find a common denominator before adding or subtracting, but for multiplication, you simply multiply the numerators and denominators directly.
-
Q: Are there other ways to visualize this multiplication? A: Yes, you could use area models to visually represent the multiplication. Imagine a square with sides of 4.5 units. Dividing it into smaller squares and rectangles can help visualize the calculation.
-
Q: What are some real-world examples beyond the ones mentioned? A: Calculating the amount of fabric needed for a project, determining the area of a wall to be painted, calculating the volume of a storage container, etc.
VIII. Conclusion:
The seemingly simple calculation of 4 1/2 x 4 1/2 serves as a gateway to understanding fundamental mathematical concepts related to fractions, area, and volume. Mastering these concepts is crucial for solving more complex problems in various fields, including geometry, engineering, and construction. By understanding the different methods of solving this problem and appreciating its practical applications, we gain a broader understanding of how mathematical principles are interwoven into our daily lives. Remember to practice regularly and apply these principles to real-world scenarios to further enhance your understanding and problem-solving abilities. The journey of mathematical learning is a continuous one, and every step, however small, contributes to a larger comprehension of the world around us.
Latest Posts
Latest Posts
-
Some Whole Numbers Are Irrational Numbers
Aug 27, 2025
-
Anatomy And Physiology Tutors Near Me
Aug 27, 2025
-
A Salesman Receives A Fixed Salary Of 500 Per Week
Aug 27, 2025
-
How To Find Perimeter Of An Octagon
Aug 27, 2025
-
15 Percent As A Fraction In Simplest Form
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about 4 1 2 X 4 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.