3x 4y 8 Solve For Y
faraar
Sep 08, 2025 · 6 min read
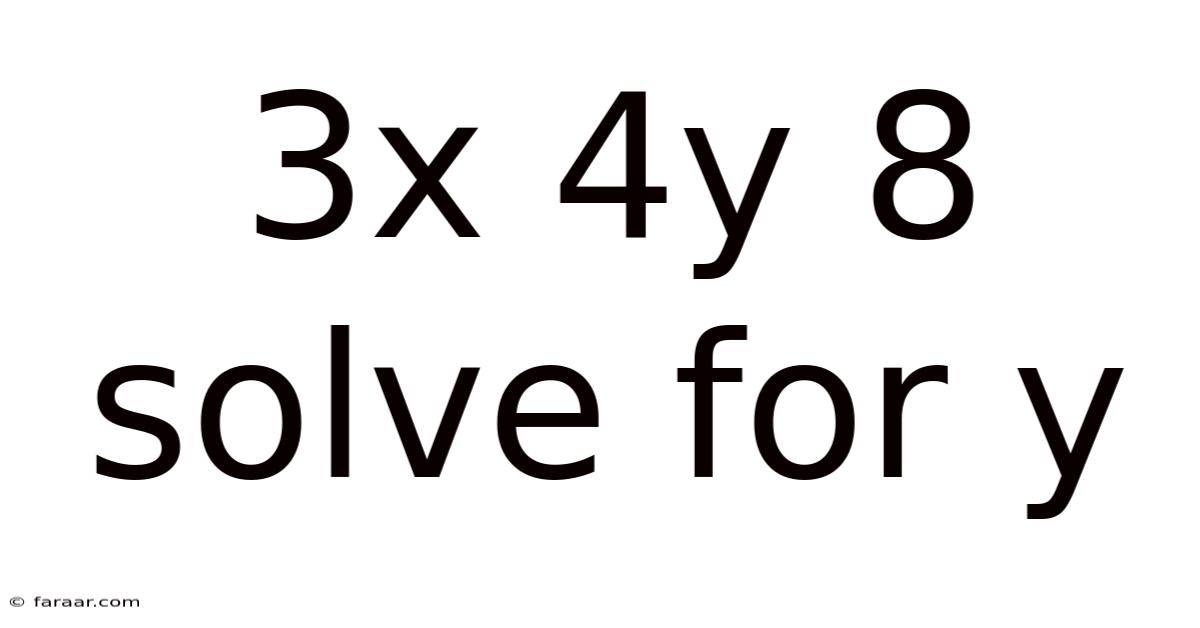
Table of Contents
Solving for Y: A Comprehensive Guide to 3x + 4y = 8
This article provides a detailed explanation of how to solve the equation 3x + 4y = 8 for y. We'll cover the fundamental algebraic steps, explore different approaches, and delve into the broader mathematical concepts involved. Understanding this seemingly simple equation unlocks a deeper understanding of linear equations, which are crucial in various fields, from physics and engineering to economics and computer science. By the end, you'll not only know how to solve for y but also grasp the underlying principles and be able to tackle similar problems with confidence.
Introduction: Understanding Linear Equations
The equation 3x + 4y = 8 is a linear equation in two variables, x and y. A linear equation represents a straight line when graphed on a coordinate plane. The goal of solving for y is to isolate y on one side of the equation, expressing it in terms of x. This gives us the equation of the line in slope-intercept form, which is typically written as y = mx + b, where m is the slope and b is the y-intercept.
Step-by-Step Solution: Isolating Y
Let's break down the process of solving 3x + 4y = 8 for y step-by-step:
-
Subtract 3x from both sides: Our first goal is to move the term containing x to the right side of the equation. To do this, we subtract 3x from both sides, maintaining the balance of the equation. This gives us:
4y = -3x + 8
-
Divide both sides by 4: Now, we need to isolate y. Since y is multiplied by 4, we divide both sides of the equation by 4:
y = (-3/4)x + 2
And there we have it! We've successfully solved for y. The equation is now in slope-intercept form (y = mx + b), where the slope (m) is -3/4 and the y-intercept (b) is 2.
Graphical Representation: Visualizing the Solution
The equation y = (-3/4)x + 2 represents a straight line. The y-intercept (2) means the line crosses the y-axis at the point (0, 2). The slope (-3/4) indicates that for every 4 units we move to the right along the x-axis, the line moves down 3 units along the y-axis. This slope signifies the rate of change of y with respect to x. Plotting these points and connecting them gives us the visual representation of our solution.
Alternative Methods: Exploring Different Approaches
While the method above is the most straightforward, there are alternative approaches to solving for y:
-
Rearranging the equation before solving: We could have started by subtracting 4y from both sides, resulting in 3x = -4y + 8. Then, we would subtract 8 from both sides (3x - 8 = -4y) and finally divide by -4 to isolate y. The result would be the same, demonstrating that different algebraic manipulations can lead to the same solution.
-
Using substitution: If we had a value for x, we could substitute that value into the original equation (3x + 4y = 8) and then solve for y. For example, if x = 4, the equation becomes 3(4) + 4y = 8, which simplifies to 12 + 4y = 8. Subtracting 12 from both sides gives 4y = -4, and dividing by 4 gives y = -1. This method is useful when dealing with systems of equations or when a specific value of x is given.
-
Matrix methods (for advanced users): For systems of linear equations with multiple variables, matrix methods like Gaussian elimination or Cramer's rule offer efficient solutions. While not necessary for this simple equation, understanding matrix methods is valuable for solving more complex linear systems.
Deeper Dive: Understanding Slope and Y-Intercept
Let's revisit the slope-intercept form, y = mx + b. We found that for our equation, m = -3/4 and b = 2.
-
Slope (m): The slope represents the rate of change of y with respect to x. In our case, a negative slope (-3/4) means that as x increases, y decreases. The slope's magnitude (3/4) indicates the steepness of the line. A larger magnitude signifies a steeper line.
-
Y-intercept (b): The y-intercept is the point where the line intersects the y-axis. This occurs when x = 0. In our equation, the y-intercept is 2, meaning the line passes through the point (0, 2).
Applications of Linear Equations: Real-World Relevance
Linear equations are fundamental to many areas of study and real-world applications:
-
Physics: Describing motion, calculating forces, and analyzing electrical circuits.
-
Engineering: Modeling relationships between variables in design and construction.
-
Economics: Analyzing supply and demand, predicting economic trends, and building economic models.
-
Computer Science: Developing algorithms, creating graphical representations, and solving optimization problems.
-
Data Science: Performing linear regression to model relationships between variables in datasets.
Frequently Asked Questions (FAQ)
-
Q: Can I solve this equation for x instead of y?
A: Yes, absolutely! You would follow a similar process, isolating x on one side of the equation. The result would be an equation expressing x in terms of y.
-
Q: What if the coefficient of y is 0?
A: If the coefficient of y is 0, the equation becomes 3x = 8, which is a simple linear equation in one variable. Solving for x would give you x = 8/3. This represents a vertical line on the coordinate plane.
-
Q: What does it mean if the slope is 0?
A: A slope of 0 indicates a horizontal line. In our slope-intercept form (y = mx + b), if m = 0, the equation simplifies to y = b, representing a horizontal line at the y-coordinate b.
-
Q: How can I check my solution?
A: You can substitute your solution (y = (-3/4)x + 2) back into the original equation (3x + 4y = 8) to verify that it holds true. If both sides of the equation are equal after substitution, your solution is correct. You can also plug in several values of x and see if the corresponding y values match those predicted by your solution.
Conclusion: Mastering Linear Equations
Solving the equation 3x + 4y = 8 for y might seem like a simple task, but it lays the groundwork for understanding more complex mathematical concepts and real-world applications. By mastering the steps involved and understanding the underlying principles of linear equations, you'll build a solid foundation in algebra and enhance your problem-solving skills across various disciplines. Remember the key steps: isolate the variable you're solving for by applying inverse operations to both sides of the equation, always maintaining the balance. With practice, you’ll become proficient in solving linear equations and confidently tackling more challenging mathematical problems. Remember to visualize the solution graphically—it can often provide valuable insights into the relationships between variables.
Latest Posts
Latest Posts
-
Why Does Heat Flow From Hot To Cold
Sep 08, 2025
-
How To Calculate Mass Of Excess Reactant
Sep 08, 2025
-
How To Solve Fraction Word Problems
Sep 08, 2025
-
How To Find Slope In Standard Form
Sep 08, 2025
-
How Many Inches Are In 7 Yards
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 3x 4y 8 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.