3x 4y 12 Solve For Y
faraar
Sep 16, 2025 · 6 min read
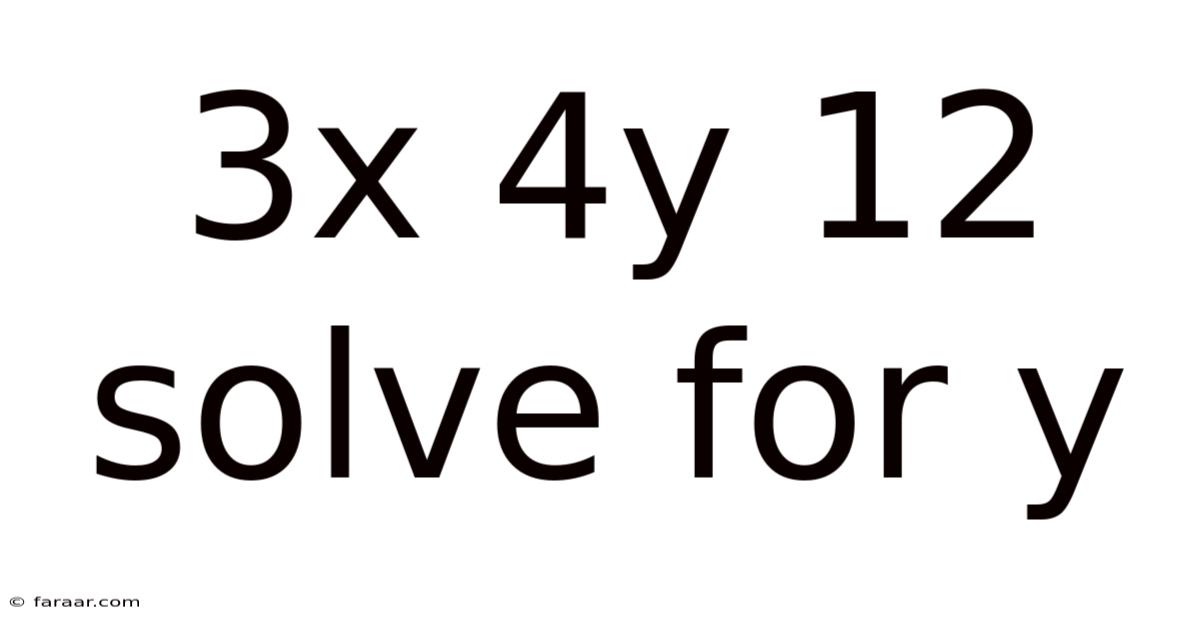
Table of Contents
Solving for 'y': A Deep Dive into 3x + 4y = 12
This article provides a comprehensive guide on how to solve the equation 3x + 4y = 12 for 'y', covering various approaches and delving into the underlying mathematical principles. We'll explore different methods, discuss their applications, and address common questions, ensuring a thorough understanding of this fundamental algebraic concept. This is crucial for anyone studying algebra, as solving for variables is a cornerstone of many mathematical operations and applications. Understanding this process lays the groundwork for tackling more complex equations in the future.
Introduction: Understanding the Equation
The equation 3x + 4y = 12 represents a linear equation in two variables, x and y. A linear equation graphs as a straight line. Solving for 'y' means isolating 'y' on one side of the equation, expressing it in terms of 'x'. This gives us a function where the value of 'y' depends on the value of 'x'. This process is fundamental to understanding the relationship between the variables and to plotting the equation on a graph.
Method 1: The Subtraction and Division Method
This is the most straightforward method for solving this particular equation. We aim to isolate 'y' by performing inverse operations.
Steps:
-
Subtract 3x from both sides: This eliminates 'x' from the left side. The equation becomes: 4y = 12 - 3x
-
Divide both sides by 4: This isolates 'y'. Remember to divide both terms on the right side by 4: y = (12 - 3x) / 4
-
Simplify (Optional): While the equation is already solved, we can simplify it further by dividing each term in the numerator by 4: y = 3 - (3/4)x
This simplified form, y = 3 - (3/4)x, is equivalent to the previous solution and is often preferred for its clarity. It clearly shows the y-intercept (3) and the slope (-3/4) of the line.
Method 2: Using the Properties of Equality
This method emphasizes the fundamental properties of equality, highlighting that any operation performed on one side of the equation must be performed on the other to maintain balance.
Steps:
-
Identify the term with 'y': This is 4y.
-
Isolate the term with 'y': Subtract 3x from both sides of the equation: 4y = 12 - 3x. This uses the subtraction property of equality.
-
Solve for 'y': Divide both sides of the equation by 4: y = (12 - 3x) / 4. This uses the division property of equality.
-
Simplify: As before, we can simplify this to y = 3 - (3/4)x.
Method 3: Rearranging the Equation
This method focuses on manipulating the equation to directly isolate 'y'. It is conceptually similar to the previous methods but emphasizes a more direct approach.
Steps:
-
Start with the original equation: 3x + 4y = 12
-
Move the term without 'y' to the right side: Subtract 3x from both sides: 4y = 12 - 3x
-
Isolate 'y': Divide both sides by 4: y = (12 - 3x) / 4
-
Simplify: Simplify the expression to y = 3 - (3/4)x
Graphical Representation and Interpretation
The solution y = 3 - (3/4)x represents a straight line. This equation is in the slope-intercept form (y = mx + b), where 'm' is the slope (-3/4) and 'b' is the y-intercept (3).
-
Slope: The slope of -3/4 indicates that for every 4-unit increase in x, y decreases by 3 units. This describes the line's inclination.
-
Y-intercept: The y-intercept of 3 indicates that the line intersects the y-axis at the point (0, 3).
Understanding the graphical representation helps visualize the relationship between x and y. For any given value of x, we can find the corresponding value of y using the equation, and plot the point on the graph.
Solving for 'x' – An Extension
While the primary focus was solving for 'y', it's beneficial to understand how to solve for 'x' as well. This demonstrates a broader understanding of manipulating linear equations.
Steps to solve for x:
-
Start with the original equation: 3x + 4y = 12
-
Isolate the term with 'x': Subtract 4y from both sides: 3x = 12 - 4y
-
Solve for 'x': Divide both sides by 3: x = (12 - 4y) / 3
-
Simplify (Optional): x = 4 - (4/3)y
Applications and Real-World Examples
Linear equations like 3x + 4y = 12 have numerous applications across various fields:
-
Economics: Modeling supply and demand relationships. 'x' could represent the price of a good, and 'y' the quantity demanded.
-
Physics: Describing relationships between physical quantities like distance, speed, and time.
-
Engineering: Representing relationships between different variables in design calculations.
-
Computer Science: Used in algorithms and data structures.
Frequently Asked Questions (FAQ)
Q: What if the equation is more complex?
A: The fundamental principles remain the same. Always focus on isolating the variable you want to solve for using inverse operations (addition/subtraction, multiplication/division). For more complex equations, you might need to use techniques like factoring or the quadratic formula.
Q: Can this equation have multiple solutions?
A: Yes, a linear equation in two variables has infinitely many solutions. Each point (x, y) that satisfies the equation is a solution.
Q: What is the difference between solving for 'y' and finding the roots?
A: Solving for 'y' expresses 'y' in terms of 'x', giving you a function. Finding the roots involves finding the values of x and y where the equation equals zero (where the line intersects the x and y axes).
Q: What if the coefficient of 'y' is zero?
A: If the coefficient of 'y' is zero (e.g., 3x + 0y = 12), then 'y' can take any value, and the equation simplifies to 3x = 12, allowing you to solve directly for 'x'.
Q: Why is understanding this important?
A: Solving linear equations is a foundational skill in mathematics and science. Mastering this technique enables you to tackle more complex problems and understand relationships between variables in various contexts.
Conclusion: Mastering the Fundamentals
Solving the equation 3x + 4y = 12 for 'y' is a fundamental algebraic skill. We’ve explored three different methods, emphasizing the underlying principles of equality and inverse operations. Understanding these methods not only helps solve this specific problem but also equips you with the tools to tackle more challenging equations and real-world applications. Remember, the key is to systematically isolate the variable you want to solve for, using the properties of equality to maintain balance throughout the process. The ability to manipulate and solve equations is essential for success in higher-level mathematics and numerous STEM fields. Practice is key; the more you solve these types of problems, the more confident and proficient you will become.
Latest Posts
Latest Posts
-
Boyles Law Describes The Relationship Between The
Sep 16, 2025
-
How To Change Slope Intercept Form Into Standard Form
Sep 16, 2025
-
6 To The Power Of 3
Sep 16, 2025
-
How Do You Find A Hole In A Graph
Sep 16, 2025
-
Rewrite 9x 81 Using A Common Factor
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3x 4y 12 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.