3x 2y 4 In Slope Intercept Form
faraar
Sep 11, 2025 · 5 min read
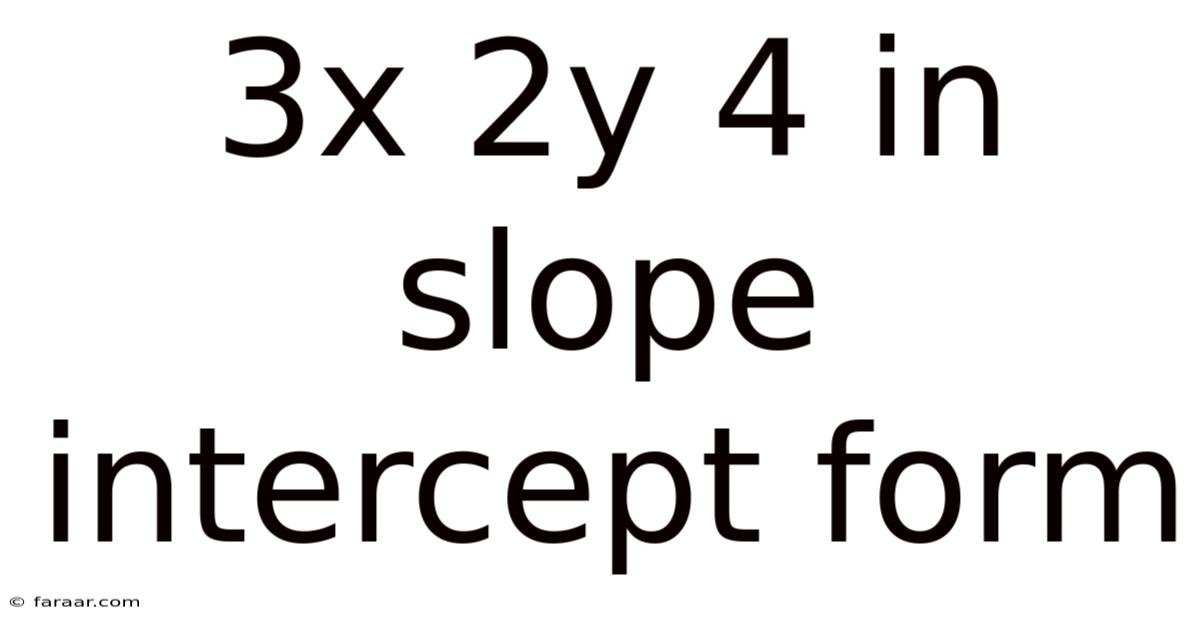
Table of Contents
Converting 3x + 2y = 4 into Slope-Intercept Form: A Comprehensive Guide
Understanding linear equations is fundamental to algebra and numerous applications in various fields. One crucial skill is transforming equations between different forms, offering diverse perspectives and facilitating problem-solving. This article provides a detailed explanation of how to convert the equation 3x + 2y = 4 into slope-intercept form (y = mx + b), clarifying each step and delving into the underlying mathematical concepts. We'll also explore the significance of slope and y-intercept, and answer frequently asked questions to ensure a thorough understanding.
Introduction: Understanding Linear Equations and Their Forms
A linear equation represents a straight line on a graph. It's typically expressed in variables, usually x and y, representing coordinates on a Cartesian plane. Several forms exist to represent linear equations, each offering unique insights:
- Standard Form: Ax + By = C, where A, B, and C are constants. The given equation, 3x + 2y = 4, is in standard form.
- Slope-Intercept Form: y = mx + b, where 'm' represents the slope (the steepness of the line) and 'b' represents the y-intercept (the point where the line crosses the y-axis).
- Point-Slope Form: y - y1 = m(x - x1), where (x1, y1) is a point on the line and 'm' is the slope.
Converting between these forms is a valuable algebraic skill. The slope-intercept form is particularly useful because it directly reveals the line's slope and y-intercept, making it easier to graph and analyze.
Steps to Convert 3x + 2y = 4 to Slope-Intercept Form
The goal is to isolate y on one side of the equation, transforming the standard form (3x + 2y = 4) into the slope-intercept form (y = mx + b). Here's a step-by-step breakdown:
1. Subtract 3x from both sides:
This step aims to move the term containing x to the right side of the equation.
3x + 2y - 3x = 4 - 3x
This simplifies to:
2y = -3x + 4
2. Divide both sides by 2:
To isolate y, we need to divide both sides of the equation by the coefficient of y, which is 2.
(2y)/2 = (-3x + 4)/2
This simplifies to:
y = (-3/2)x + 2
3. Result: Slope-Intercept Form
The equation is now in slope-intercept form: y = (-3/2)x + 2
This tells us that the slope (m) of the line is -3/2, and the y-intercept (b) is 2.
Explanation of Slope and Y-Intercept
Let's break down the meaning of the slope and y-intercept we derived:
-
Slope (m = -3/2): The slope represents the rate of change of y with respect to x. A negative slope indicates that as x increases, y decreases. The value -3/2 means that for every 2 units increase in x, y decreases by 3 units. This signifies a downward-sloping line. The slope also defines the angle of inclination of the line with respect to the x-axis.
-
Y-intercept (b = 2): The y-intercept is the point where the line intersects the y-axis (where x = 0). In this case, the y-intercept is 2, meaning the line passes through the point (0, 2).
Graphing the Equation
Now that we have the equation in slope-intercept form (y = (-3/2)x + 2), graphing it is straightforward:
-
Plot the y-intercept: Start by plotting the point (0, 2) on the y-axis.
-
Use the slope to find another point: The slope is -3/2. This means from the y-intercept (0, 2), move 2 units to the right and 3 units down to find another point on the line (2, -1). You could also move 2 units to the left and 3 units up to find another point (-2, 5).
-
Draw the line: Draw a straight line passing through these points. This line represents the equation 3x + 2y = 4.
Further Applications and Extensions
The slope-intercept form offers numerous advantages beyond graphing. It's crucial for:
- Predicting values: Given an x value, you can easily calculate the corresponding y value using the equation.
- Comparing lines: By comparing slopes and y-intercepts, you can determine if lines are parallel (same slope, different y-intercept), perpendicular (slopes are negative reciprocals), or neither.
- Solving systems of equations: The slope-intercept form simplifies solving systems of linear equations graphically (finding the point of intersection).
- Real-world modeling: Linear equations model many real-world phenomena, such as distance-time relationships, cost functions, and population growth.
Frequently Asked Questions (FAQ)
Q1: What if the coefficient of y is negative?
If the coefficient of y is negative in the standard form, the process remains the same. However, when you divide both sides by the coefficient, remember to change the signs of all terms on the other side of the equation.
Q2: Can I convert from slope-intercept form back to standard form?
Yes. To convert from y = mx + b to Ax + By = C, simply move the 'mx' term to the left side and ensure that A, B, and C are integers (whole numbers). You may need to multiply the entire equation by a common denominator to eliminate fractions.
Q3: What happens if the slope is undefined?
An undefined slope indicates a vertical line. Vertical lines have the equation x = k, where k is a constant. This form cannot be expressed in slope-intercept form because the slope is infinite.
Q4: How can I check my work after converting the equation?
After converting the equation, you can substitute a point from the original equation into the new slope-intercept equation to verify if it satisfies the equation. If it does, your conversion is likely correct.
Conclusion: Mastering Linear Equation Transformations
Converting linear equations between different forms, particularly from standard form to slope-intercept form, is a vital algebraic skill. The process involves algebraic manipulations to isolate the variable y, revealing the slope and y-intercept, which offer crucial insights into the line's characteristics and behaviour. This ability is essential for graphing, analyzing, and applying linear equations to various mathematical and real-world problems. Understanding the concepts of slope and y-intercept deepens your comprehension of linear relationships and lays a strong foundation for more advanced mathematical concepts. By consistently practicing these techniques, you'll develop confidence and proficiency in handling linear equations effectively.
Latest Posts
Latest Posts
-
Positive Negative Zero And Undefined Slope
Sep 11, 2025
-
What Is The Coefficient Of H2o
Sep 11, 2025
-
How Many Molecules Are In 25 Grams Of Nh3
Sep 11, 2025
-
How Many 9 Are In A Deck Of Cards
Sep 11, 2025
-
Average Par On A Golf Course
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3x 2y 4 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.