3x 2y 10 In Slope Intercept Form
faraar
Sep 19, 2025 · 7 min read
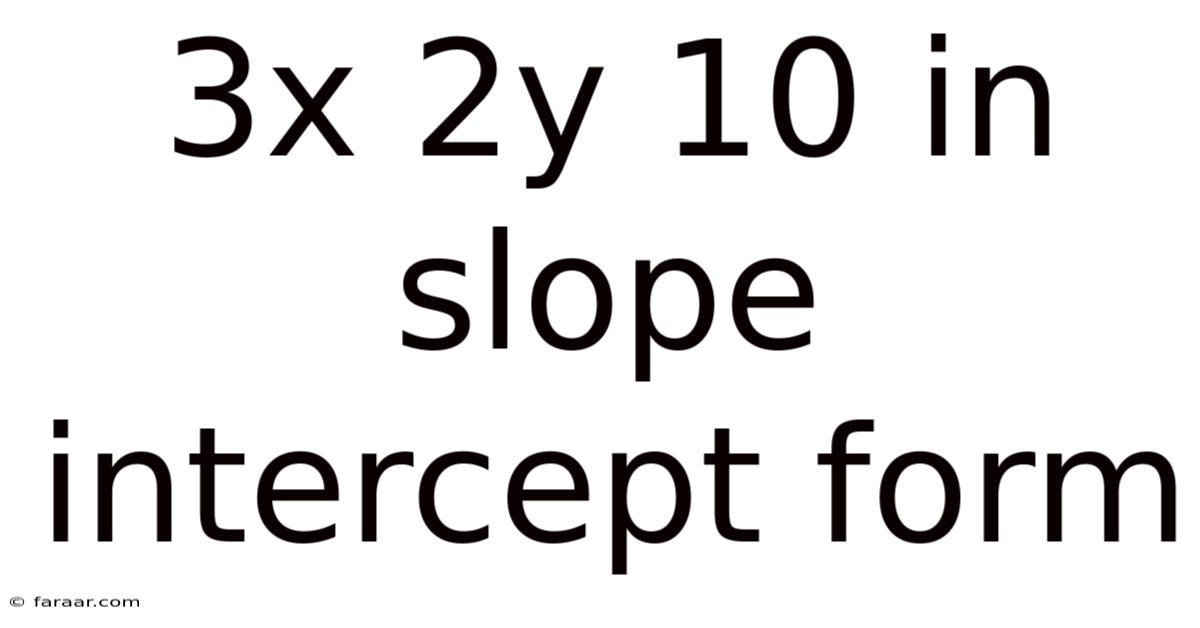
Table of Contents
Transforming 3x + 2y = 10 into Slope-Intercept Form: A Comprehensive Guide
Understanding the slope-intercept form of a linear equation is crucial in algebra and beyond. This form, y = mx + b, allows us to easily identify the slope (m) and the y-intercept (b) of a line, providing valuable insights into its characteristics and graphical representation. This article will guide you through the process of converting the equation 3x + 2y = 10 into slope-intercept form, explaining the steps involved and providing additional context to solidify your understanding. We'll delve into the concepts of slope, y-intercept, and how they relate to the equation of a line, offering a comprehensive exploration for students of all levels.
Understanding the Slope-Intercept Form (y = mx + b)
Before we begin transforming the equation, let's refresh our understanding of the slope-intercept form: y = mx + b.
- y: Represents the y-coordinate of any point on the line.
- x: Represents the x-coordinate of any point on the line.
- m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope indicates an upward-sloping line (from left to right), while a negative slope indicates a downward-sloping line. A slope of zero represents a horizontal line, and an undefined slope represents a vertical line. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept. This is the point where the line intersects the y-axis (where x = 0).
Step-by-Step Conversion: 3x + 2y = 10 to Slope-Intercept Form
Our goal is to rearrange the equation 3x + 2y = 10 so that it matches the slope-intercept form, y = mx + b. Here's how we do it:
Step 1: Isolate the y-term
Our first step is to isolate the term containing 'y' on one side of the equation. To do this, we subtract 3x from both sides:
3x + 2y - 3x = 10 - 3x
This simplifies to:
2y = -3x + 10
Step 2: Solve for y
Now, we need to solve for 'y' by dividing both sides of the equation by 2:
2y / 2 = (-3x + 10) / 2
This simplifies to:
y = - (3/2)x + 5
Step 3: Identify the Slope and y-intercept
Now that our equation is in the slope-intercept form (y = mx + b), we can easily identify the slope and y-intercept:
-
Slope (m) = -3/2: This tells us that the line slopes downwards (because it's negative) and for every 2 units we move to the right along the x-axis, we move 3 units down along the y-axis.
-
y-intercept (b) = 5: This tells us that the line intersects the y-axis at the point (0, 5).
Therefore, the slope-intercept form of the equation 3x + 2y = 10 is y = -(3/2)x + 5.
Graphical Representation and Interpretation
The slope-intercept form provides a straightforward way to graph the linear equation. We know the y-intercept is 5, so we can plot the point (0, 5) on the y-axis. Using the slope (-3/2), we can find another point on the line. Since the slope is -3/2, we can move 2 units to the right and 3 units down from the y-intercept (0, 5) to find another point (2, 2). By connecting these two points, we obtain the graph of the line representing the equation 3x + 2y = 10.
This graphical representation further reinforces our understanding of the slope and y-intercept. The downward slope is visually evident, and the line clearly intersects the y-axis at 5.
Further Applications and Extensions
Understanding the slope-intercept form is fundamental to solving various problems in algebra and beyond. Here are some key applications:
-
Finding points on the line: By substituting any x-value into the equation y = -(3/2)x + 5, we can easily calculate the corresponding y-value, giving us a point on the line.
-
Determining parallel and perpendicular lines: Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other. Knowing the slope of our line (-3/2) allows us to quickly determine the slopes of lines parallel or perpendicular to it.
-
Solving systems of equations: The slope-intercept form is invaluable when solving systems of linear equations graphically or algebraically. By comparing the slopes and y-intercepts of two lines, we can determine if they intersect (one solution), are parallel (no solution), or are coincident (infinitely many solutions).
-
Real-world applications: Linear equations in slope-intercept form are widely used to model real-world scenarios involving linear relationships, such as calculating distances, speeds, costs, and profits.
Common Mistakes and How to Avoid Them
While the conversion process is relatively straightforward, some common mistakes can occur:
-
Incorrectly isolating the y-term: Ensure that you perform the same operations on both sides of the equation to maintain balance. Common errors include adding or subtracting incorrectly or dividing only one side of the equation.
-
Mistakes with signs: Pay close attention to the signs of the coefficients. A misplaced negative sign can drastically alter the slope and y-intercept.
-
Improper simplification: Always simplify fractions and combine like terms to obtain the most accurate slope-intercept form.
-
Forgetting to divide all terms: When dividing to isolate y, remember to divide every term on both sides of the equation by the coefficient of y.
By carefully reviewing each step and double-checking your work, you can minimize these errors.
Frequently Asked Questions (FAQ)
Q1: What if the coefficient of y is negative?
A1: If the coefficient of y is negative, you'll still follow the same steps. However, remember to account for the negative sign when dividing both sides of the equation to solve for y. The resulting slope will also be affected by this negative sign.
Q2: Can any linear equation be converted into slope-intercept form?
A2: Yes, any linear equation that is not a vertical line (x = constant) can be converted into slope-intercept form. Vertical lines have undefined slopes and cannot be expressed in the y = mx + b form.
Q3: What if the equation is already in slope-intercept form?
A3: If the equation is already in slope-intercept form (y = mx + b), there's no need for conversion. The slope (m) and y-intercept (b) are readily apparent.
Q4: How can I check my work?
A4: You can check your work by substituting the coordinates of a point from your graph into the original equation (3x + 2y = 10) and verifying if it satisfies the equation. You can also graph your slope-intercept form equation and compare it to a graph of the original equation. The graphs should be identical.
Q5: What are some other forms of linear equations?
A5: Besides the slope-intercept form, other common forms include the standard form (Ax + By = C), the point-slope form (y - y1 = m(x - x1)), and the intercept form (x/a + y/b = 1). Each form offers a different perspective and is useful in various contexts.
Conclusion
Converting the equation 3x + 2y = 10 into slope-intercept form is a fundamental algebraic skill. By understanding the steps involved and the meaning of the slope and y-intercept, we can easily represent this linear equation graphically and utilize it to solve various mathematical problems. Remember to pay close attention to the signs and to divide all terms when solving for 'y'. With practice, you'll confidently navigate this crucial concept and apply it to more complex scenarios. The key is to understand the underlying principles and to approach each step methodically. This thorough understanding will empower you to tackle more advanced topics in algebra and beyond.
Latest Posts
Latest Posts
-
How Many Square Feet Is 10x20
Sep 19, 2025
-
How To Find Length And Width From Area
Sep 19, 2025
-
How To Find Interval Notation On A Graph
Sep 19, 2025
-
Mass Of A Neutron In Grams
Sep 19, 2025
-
162 Square Meter In Square Feet
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3x 2y 10 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.