3x 1 5y 7 Solve For Y
faraar
Aug 27, 2025 · 5 min read
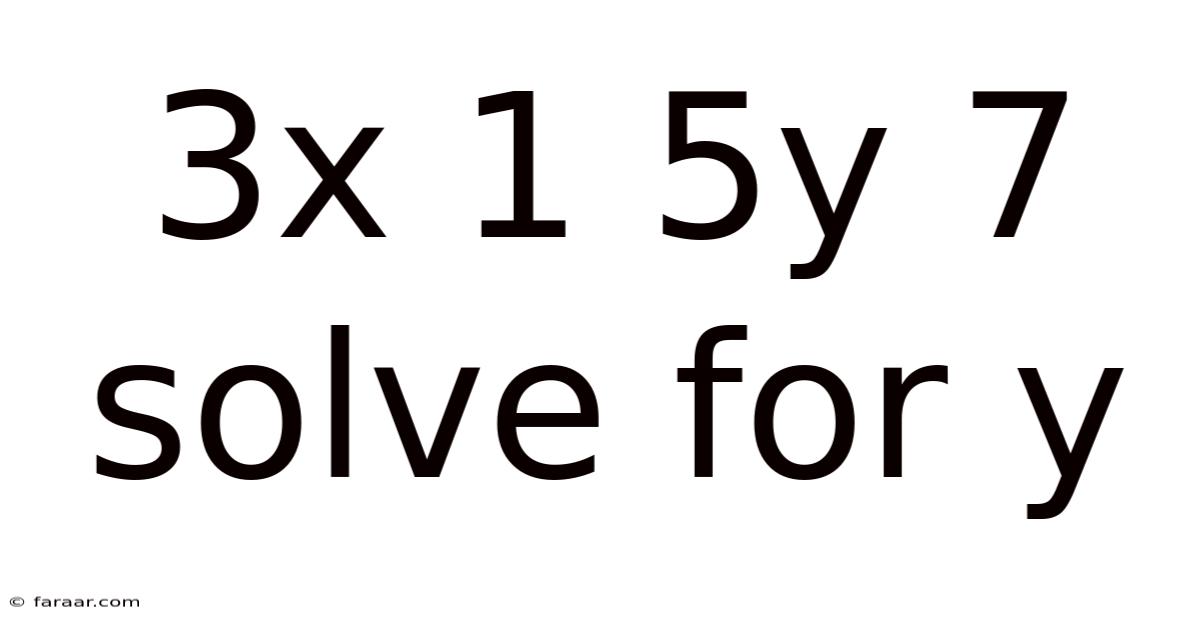
Table of Contents
Solving for Y: A Comprehensive Guide to 3x + 1 = 5y + 7
This article provides a detailed explanation on how to solve the algebraic equation 3x + 1 = 5y + 7 for y. We'll break down the process step-by-step, ensuring a clear understanding, regardless of your prior algebra experience. We will also explore different approaches and discuss the significance of isolating variables in equation solving. This guide will not only teach you how to solve this specific equation but also equip you with the fundamental skills to tackle similar problems.
Understanding the Equation
Before we begin solving, let's understand what the equation 3x + 1 = 5y + 7 represents. This is a linear equation with two variables, x and y. A linear equation means the highest power of the variables is 1. The equation describes a relationship between x and y; for every value of x, there's a corresponding value of y that satisfies the equation. Our goal is to isolate y, expressing it in terms of x. This means we want to rewrite the equation in the form y = ...
Step-by-Step Solution: Isolating Y
The key to solving for y is to manipulate the equation using algebraic operations, ensuring we maintain the equality. Here's the step-by-step process:
-
Subtract 7 from both sides: Our first step is to simplify the equation by removing the constant term on the right-hand side. Subtracting 7 from both sides maintains the equality:
3x + 1 - 7 = 5y + 7 - 7
This simplifies to:
3x - 6 = 5y
-
Divide both sides by 5: Now, we need to isolate y by dividing both sides of the equation by its coefficient, which is 5:
(3x - 6) / 5 = (5y) / 5
This simplifies to:
(3x - 6) / 5 = y
-
Rewrite the equation: It's good practice to rewrite the equation with y on the left-hand side:
y = (3x - 6) / 5
This is our final solution. We have successfully expressed y in terms of x. This means for any given value of x, we can substitute it into the equation y = (3x - 6) / 5 to find the corresponding value of y that satisfies the original equation.
Understanding the Solution: What does y = (3x - 6)/5 mean?
The equation y = (3x - 6) / 5 represents a linear relationship between x and y. It's a function where x is the independent variable and y is the dependent variable. This means the value of y depends on the value of x.
Let's illustrate with a few examples:
- If x = 2: y = (3 * 2 - 6) / 5 = 0
- If x = 0: y = (3 * 0 - 6) / 5 = -6/5 = -1.2
- If x = 5: y = (3 * 5 - 6) / 5 = 9/5 = 1.8
- If x = -1: y = (3 * -1 - 6) / 5 = -9/5 = -1.8
Each of these (x, y) pairs satisfies the original equation, 3x + 1 = 5y + 7. You can verify this by substituting the values back into the original equation.
Alternative Approach: Solving using Substitution
While the previous method is the most straightforward, we can also approach this problem using substitution. This method is particularly useful when dealing with systems of equations. However, in this case, it adds an unnecessary step.
Let's assume we have a value for x. For example, let's say x = 4. We can substitute this value into the original equation:
3(4) + 1 = 5y + 7
13 = 5y + 7
Then, we solve for y as before:
6 = 5y
y = 6/5 = 1.2
This confirms that when x = 4, y = 1.2 satisfies the equation. However, this method doesn't give us the general solution in terms of x, which is what we achieved with the first method.
The Importance of Isolating Variables
Isolating variables, as we did with y in this example, is a fundamental skill in algebra. It allows us to:
- Find specific solutions: Given a value for one variable, we can easily calculate the corresponding value for the other.
- Graph the equation: The equation y = (3x - 6) / 5 is in slope-intercept form (y = mx + b), making it easy to graph. The slope is 3/5 and the y-intercept is -6/5.
- Analyze the relationship between variables: The equation shows the direct relationship between x and y. An increase in x leads to a corresponding change in y.
- Solve more complex equations: The ability to isolate variables is crucial for solving systems of equations and more advanced algebraic problems.
Frequently Asked Questions (FAQ)
-
Q: Can I solve for x instead of y?
A: Yes, absolutely! You would follow a similar process, but the steps would be different. You would need to isolate x by first subtracting 1 from both sides, then subtracting 5y from both sides, and finally dividing by 3. The resulting equation would be x = (5y + 6) / 3.
-
Q: What if the equation was more complex, with more terms or higher powers?
A: The fundamental principles remain the same. You would still use algebraic operations (addition, subtraction, multiplication, division) to isolate the variable you want to solve for. However, more complex equations may require additional steps and techniques such as factoring or using the quadratic formula.
-
Q: What if there are no solutions to the equation?
A: In some cases, an equation might have no solution or infinitely many solutions. This would usually occur if the equation simplifies to a contradiction (e.g., 0 = 5) or an identity (e.g., 2x = 2x). Our equation, however, has infinitely many solutions, since for every value of x, there is a corresponding value of y.
-
Q: How can I check my answer?
A: Always check your solution by substituting your answer back into the original equation. If the left-hand side equals the right-hand side, then your solution is correct. For example, if you found y = 2, substitute it back into 3x + 1 = 5y + 7 to see if it holds true.
Conclusion
Solving the equation 3x + 1 = 5y + 7 for y involves applying fundamental algebraic principles to isolate the variable. The solution, y = (3x - 6) / 5, demonstrates a linear relationship between x and y. Understanding how to solve this type of equation is essential for mastering basic algebra and tackling more advanced mathematical concepts. Remember the importance of isolating variables, checking your work, and understanding the meaning of your solution within the context of the problem. This process not only helps solve this specific equation but lays a solid foundation for future algebraic endeavors.
Latest Posts
Latest Posts
-
How Many Protons Neutrons And Electrons Does Mg Have
Aug 27, 2025
-
A Local Ice Cream Shop Sells
Aug 27, 2025
-
10 Less Than J Is 35
Aug 27, 2025
-
Is The Number 31 Prime Or Composite
Aug 27, 2025
-
What Is 1 3 Of A Mile
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about 3x 1 5y 7 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.