35 Is 5 Of What Number
faraar
Sep 03, 2025 · 5 min read
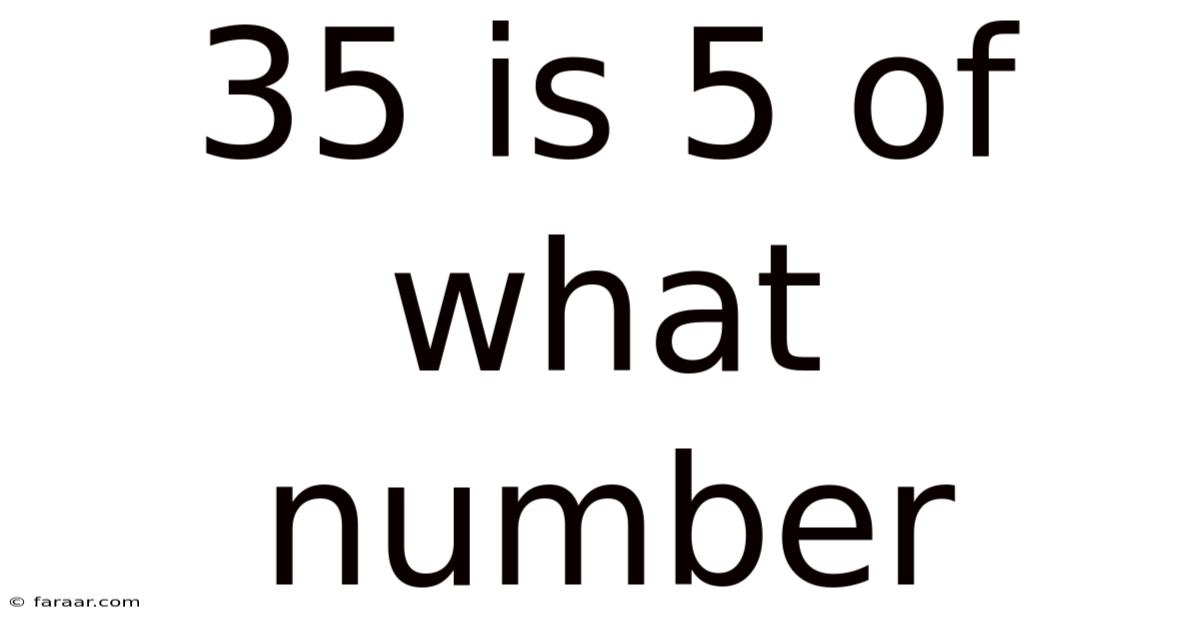
Table of Contents
35 is 5% of What Number? Unlocking the Power of Percentages
Finding a percentage of a number is a fundamental mathematical concept used daily in various contexts, from calculating discounts and taxes to understanding statistical data and analyzing financial reports. This article will delve into the process of determining the original number when you know a percentage of it, specifically addressing the question: "35 is 5% of what number?". We'll explore the solution using different methods, providing a thorough understanding of the underlying principles and offering practical applications. This will empower you to confidently tackle similar percentage problems in your daily life and studies.
Understanding the Basics of Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 5% means 5 out of 100, or 5/100, which simplifies to 1/20 as a fraction and 0.05 as a decimal. Understanding this fundamental relationship between percentages, fractions, and decimals is crucial for solving percentage problems.
Method 1: Using the Equation Method
The most direct way to solve "35 is 5% of what number?" is by setting up an algebraic equation. Let's represent the unknown number as 'x'. We can translate the problem into an equation as follows:
5% of x = 35
Converting 5% to a decimal (0.05), we get:
0.05x = 35
To solve for 'x', we need to isolate it by dividing both sides of the equation by 0.05:
x = 35 / 0.05
x = 700
Therefore, 35 is 5% of 700.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as a proportion:
5/100 = 35/x
This proportion reads: "5 is to 100 as 35 is to x." To solve for 'x', we cross-multiply:
5x = 100 * 35
5x = 3500
Now, divide both sides by 5:
x = 3500 / 5
x = 700
Again, we find that 35 is 5% of 700.
Method 3: Working Backwards from the Percentage
This method involves a more intuitive approach. If 35 represents 5% of a number, we can first determine what 1% of that number would be. Since 5% is equivalent to five 1% increments, we simply divide 35 by 5:
35 / 5 = 7
This means 1% of the unknown number is 7. To find the total number (100%), we multiply this value by 100:
7 * 100 = 700
Therefore, confirming our previous results, 35 is 5% of 700.
Illustrative Examples: Real-World Applications
Let's consider some real-world scenarios to further illustrate the application of this concept.
-
Sales and Discounts: A store offers a 5% discount on an item, and the discount amount is $35. Using the methods described above, we can determine the original price of the item was $700.
-
Tax Calculations: If a sales tax of 5% adds $35 to the cost of a purchase, the original price before tax was $700.
-
Statistical Analysis: In a survey, 5% of respondents (35 people) chose a particular option. The total number of respondents was 700.
-
Investment Returns: If an investment yields a 5% return of $35, the initial investment amount was $700.
These examples showcase the practicality and versatility of understanding percentage calculations in diverse everyday situations.
Understanding Percentage Increase and Decrease
It's important to differentiate between finding a percentage of a number and calculating a percentage increase or decrease. While the problem "35 is 5% of what number?" involves finding the original amount from a given percentage, percentage increase/decrease problems involve finding the new amount after an increase or decrease. For example:
-
Percentage Increase: If a price increases by 5%, we would add 5% of the original price to the original price to find the new price.
-
Percentage Decrease: If a price decreases by 5%, we would subtract 5% of the original price from the original price to find the new price.
Understanding this distinction is crucial for accurately applying percentage calculations in different contexts.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Calculators are invaluable tools for solving percentage problems, especially those involving more complex calculations or larger numbers. Most calculators have a percentage function (%) that simplifies the process.
Q: What if the percentage is a decimal or a fraction?
A: Convert the percentage to a decimal before applying any of the methods. For example, 12.5% becomes 0.125, and 1/4% becomes 0.0025.
Q: How can I check my answer to ensure accuracy?
A: Always verify your answer by plugging the calculated value back into the original problem. In this case, calculating 5% of 700 should equal 35.
Q: Are there other methods to solve percentage problems?
A: While the methods described above are the most common and straightforward, other approaches using more advanced mathematical concepts might be used in more complex scenarios. However, for basic percentage calculations, these three methods are sufficient.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems like "35 is 5% of what number?" is a valuable skill with wide-ranging applications. By understanding the fundamental concepts of percentages, fractions, and decimals, and by mastering the various solution methods (equation method, proportion method, working backwards), you can confidently tackle percentage problems in any context. Remember to practice regularly and apply these methods to real-world scenarios to reinforce your understanding and build your problem-solving skills. This comprehensive guide provides a strong foundation for further exploration into the world of percentages and their diverse applications in mathematics and beyond. The ability to confidently handle percentage calculations will significantly enhance your analytical and problem-solving skills, proving to be an asset in various academic and professional pursuits. Continue practicing, and you'll master this essential mathematical skill in no time.
Latest Posts
Latest Posts
-
How Do You Write 2 5 As A Fraction
Sep 04, 2025
-
Is The Ghost In Hamlet Real
Sep 04, 2025
-
How To Find Y Intercept From Points
Sep 04, 2025
-
A Pe Rt Solve For R
Sep 04, 2025
-
Find All Values Of X For Which The Series Converges
Sep 04, 2025
Related Post
Thank you for visiting our website which covers about 35 Is 5 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.