3 Less Than The Square Of A Number.
faraar
Sep 10, 2025 · 6 min read
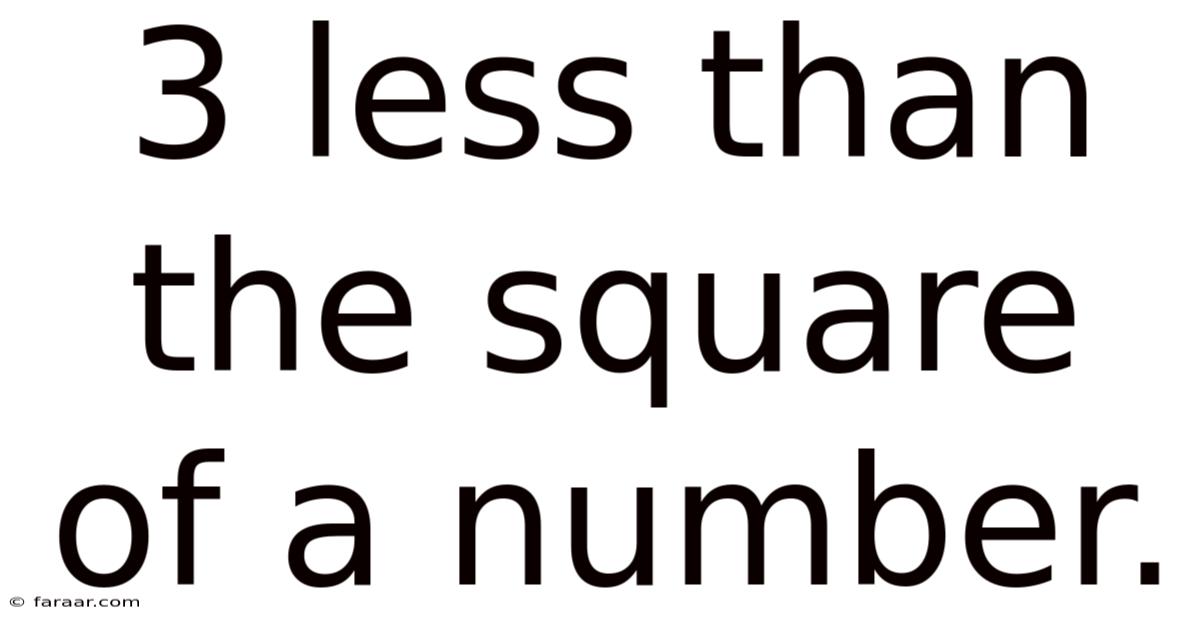
Table of Contents
Exploring the Mathematical Expression: 3 Less Than the Square of a Number
This article delves into the mathematical expression "3 less than the square of a number," exploring its meaning, representation, applications, and problem-solving techniques. We'll uncover the underlying concepts, examine different approaches to solving related problems, and address common questions and misconceptions. Understanding this seemingly simple expression unlocks a pathway to deeper mathematical comprehension and problem-solving skills. This exploration is crucial for students of algebra and beyond, providing a solid foundation for more complex mathematical concepts.
Understanding the Expression
The phrase "3 less than the square of a number" translates directly into a mathematical expression. Let's break it down:
- "A number": This represents an unknown value, which we typically denote with a variable, such as x, y, or n.
- "The square of a number": This means the number multiplied by itself, or x², y², or n².
- "3 less than": This indicates subtraction; we subtract 3 from the square of the number.
Therefore, the complete mathematical expression is x² - 3 (or y² - 3, n² - 3, etc., depending on the chosen variable). This simple expression forms the basis for a wide range of mathematical problems.
Representing the Expression Graphically
The expression x² - 3 can be represented graphically. This visual representation provides valuable insight into the behavior of the expression for different values of x. The graph is a parabola, a U-shaped curve. The parabola opens upwards because the coefficient of the x² term is positive (1). The vertex of the parabola, which represents the minimum value of the expression, is located at (0, -3). This means the expression has a minimum value of -3 when x = 0. As x increases or decreases from 0, the value of the expression increases.
Understanding the graphical representation allows us to quickly visualize the relationship between the input (x) and the output (x² - 3). This is crucial for solving problems involving inequalities or finding the range of values the expression can take. For example, we can visually determine the values of x for which x² - 3 is positive, negative, or equal to a specific value.
Solving Equations and Inequalities
The expression x² - 3 forms the core of many algebraic equations and inequalities. Let's explore several scenarios:
1. Finding the value of x when x² - 3 = 0:
This involves solving a quadratic equation. We can rearrange the equation to x² = 3, then take the square root of both sides:
x = ±√3
This means there are two solutions: x = √3 and x = -√3.
2. Finding the value of x when x² - 3 > 0:
This inequality asks us to find the values of x where the expression is greater than zero. This occurs when x² > 3. Taking the square root (and considering both positive and negative roots), we get:
x > √3 or x < -√3
This means the inequality is satisfied when x is greater than √3 or less than -√3.
3. Finding the value of x when x² - 3 < 0:
This inequality requires finding values of x where the expression is less than zero. This occurs when x² < 3. Taking the square root, we obtain:
-√3 < x < √3
This means the inequality holds true when x is between -√3 and √3.
These examples demonstrate how solving equations and inequalities involving the expression x² - 3 requires applying fundamental algebraic techniques like factoring, solving quadratic equations, and understanding the properties of inequalities.
Real-World Applications
While seemingly abstract, the expression "3 less than the square of a number" has applications in various real-world scenarios. Here are a few examples:
- Physics: In projectile motion, the vertical displacement of an object can be modeled using a quadratic equation, potentially involving a term similar to x² - 3, where x represents time.
- Engineering: The design of certain structures or components may involve quadratic relationships, requiring the use of expressions like x² - 3 to calculate dimensions or optimal performance.
- Economics: Economic models often use quadratic functions to represent cost, revenue, or profit functions, where an expression like x² - 3 might represent a simplified model.
- Computer Science: In algorithms and data structures, quadratic time complexity is often encountered, and an expression like x² - 3 can represent a simplified complexity analysis.
These are just a few examples; the application of quadratic expressions like x² - 3 is widespread across various scientific and engineering fields.
Advanced Concepts and Extensions
The simple expression x² - 3 can serve as a stepping stone to more advanced mathematical concepts:
- Completing the Square: The process of completing the square can be applied to expressions like x² - 3 to rewrite it in vertex form, which makes it easier to identify the vertex and other properties of the parabola.
- Quadratic Formula: The quadratic formula is a powerful tool for solving any quadratic equation, including equations derived from the expression x² - 3.
- Calculus: The expression x² - 3 can be differentiated and integrated, leading to the study of slopes and areas under the curve of the parabola.
- Complex Numbers: If we extend the domain of x to include complex numbers, the expression x² - 3 will have solutions beyond real numbers.
These advanced concepts build upon the foundational understanding of the simple expression x² - 3, showcasing its significance in broader mathematical contexts.
Frequently Asked Questions (FAQ)
Q1: What is the difference between "3 less than the square of a number" and "the square of a number less 3"?
A1: There is no difference. Both phrases translate to the same mathematical expression: x² - 3.
Q2: Can x² - 3 ever be negative?
A2: Yes. The expression x² - 3 is negative when -√3 < x < √3.
Q3: What is the vertex of the parabola represented by y = x² - 3?
A3: The vertex is at (0, -3).
Q4: How do I solve an equation like x² - 3 = 7?
A4: Add 3 to both sides to get x² = 10, then take the square root of both sides to get x = ±√10.
Q5: What are the roots of the equation x² - 3 = 0?
A5: The roots are x = √3 and x = -√3.
Conclusion
The seemingly simple expression "3 less than the square of a number" (or x² - 3) serves as a powerful gateway to understanding fundamental algebraic concepts, graphical representations, problem-solving techniques, and more advanced mathematical principles. This exploration demonstrates how a seemingly simple concept can have profound implications across various mathematical fields and real-world applications. By understanding this expression thoroughly, students build a solid foundation for future success in mathematics and related disciplines. The journey from interpreting a phrase to understanding its graphical representation, solving equations and inequalities based on it, and finally grasping its applications in various fields showcases the beauty and power of mathematical reasoning. This journey highlights that even the simplest expressions hold a world of mathematical possibilities waiting to be explored.
Latest Posts
Latest Posts
-
Mass Of 50 Ml Of Water
Sep 10, 2025
-
Is Pre Algebra The Same As Algebra 1
Sep 10, 2025
-
Factor The Expression Completely Over The Complex Numbers Y4 12y2 36
Sep 10, 2025
-
Use A Reference Triangle To Find The Given Angle
Sep 10, 2025
-
To Change From One Form To Another
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3 Less Than The Square Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.