3 Divided By 1/5 As A Fraction
faraar
Sep 07, 2025 · 5 min read
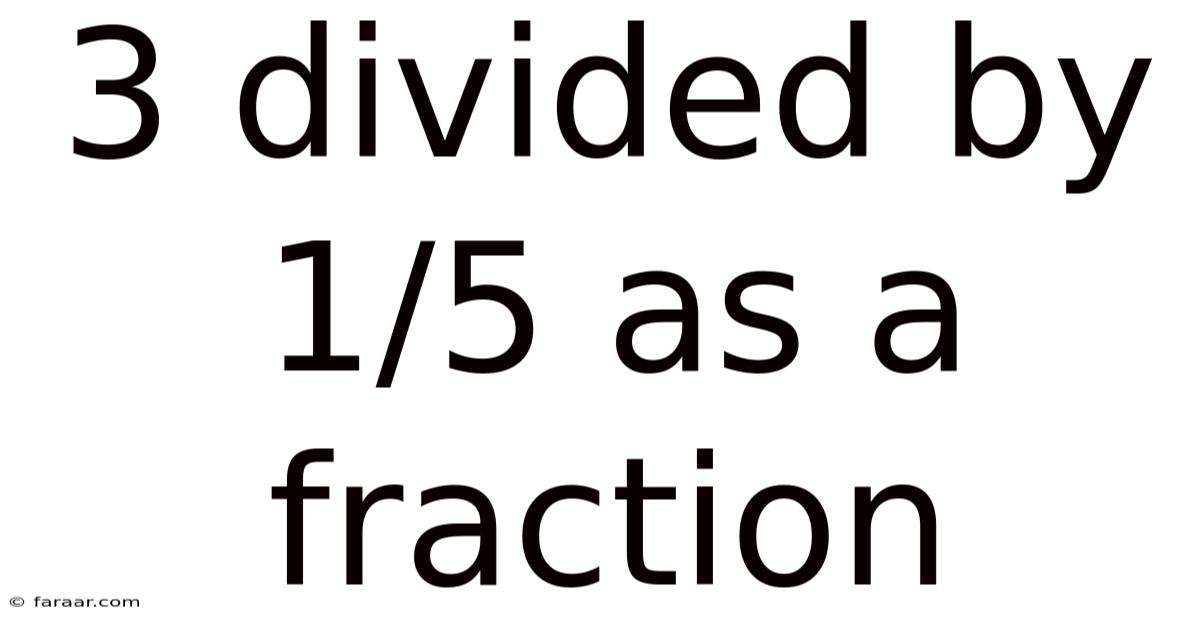
Table of Contents
3 Divided by 1/5 as a Fraction: A Comprehensive Guide
Dividing by fractions can seem tricky at first, but with a little understanding, it becomes straightforward. This article will thoroughly explain how to solve 3 divided by 1/5 as a fraction, providing a step-by-step guide, scientific explanations, and addressing frequently asked questions. We'll also explore the underlying mathematical principles to solidify your understanding of fraction division. By the end, you’ll not only know the answer but also confidently tackle similar problems.
Understanding Fraction Division: The Basics
Before diving into our specific problem (3 ÷ 1/5), let's refresh our understanding of fraction division. The core concept revolves around the idea of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 1/5 is 5/1 (or simply 5).
The rule for dividing fractions is to multiply the first fraction by the reciprocal of the second fraction. This means:
a/b ÷ c/d = a/b × d/c
This rule is fundamental and applies to all fraction division problems, regardless of complexity. Remember, any whole number can be expressed as a fraction by placing it over 1 (e.g., 3 = 3/1).
Solving 3 Divided by 1/5 Step-by-Step
Now, let's apply this knowledge to our problem: 3 divided by 1/5 (3 ÷ 1/5).
Step 1: Express the whole number as a fraction.
We begin by expressing the whole number 3 as a fraction: 3/1.
Step 2: Find the reciprocal of the second fraction.
The second fraction is 1/5. Its reciprocal is 5/1 (or simply 5).
Step 3: Multiply the first fraction by the reciprocal of the second fraction.
Now, we multiply the fractions:
(3/1) × (5/1) = (3 × 5) / (1 × 1) = 15/1
Step 4: Simplify the resulting fraction.
15/1 simplifies to 15.
Therefore, 3 divided by 1/5 is equal to 15.
Visualizing the Problem: A Real-World Analogy
Imagine you have 3 pizzas, and you want to divide each pizza into fifths (1/5). How many slices do you have in total?
Each pizza yields 5 slices (3 pizzas × 5 slices/pizza = 15 slices). This visual representation reinforces the mathematical calculation and provides a concrete understanding of the result.
The Scientific Explanation: Why Does This Work?
The method of inverting and multiplying isn't just a trick; it's rooted in the fundamental principles of division. Division is essentially the inverse operation of multiplication. When we divide a by b, we're asking, "How many times does b fit into a?"
Let's consider the problem 3 ÷ 1/5 in this light. We're asking, "How many times does 1/5 fit into 3?" To answer this, we need to determine how many 1/5 portions are contained within 3 whole units. By multiplying 3 by the reciprocal (5), we're effectively scaling up the number of fifths to determine the total number of pieces.
Exploring Related Concepts: Complex Fraction Division
Once you grasp the basics, you can tackle more complex problems involving fractions. For example, let’s consider dividing a fraction by another fraction:
(2/3) ÷ (1/4)
Following the same steps:
- Keep the first fraction the same: 2/3
- Find the reciprocal of the second fraction: 4/1
- Multiply: (2/3) x (4/1) = 8/3
The answer is 8/3, which can also be expressed as a mixed number (2 2/3).
Frequently Asked Questions (FAQ)
Q1: Why do we invert and multiply when dividing fractions?
A1: Inverting and multiplying is a shortcut based on the fundamental principle of division as the inverse of multiplication. It simplifies the calculation and avoids the complexities of working directly with complex fractions.
Q2: Can I divide fractions using a calculator?
A2: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving, especially when dealing with more complex scenarios.
Q3: What if the result is an improper fraction?
A3: An improper fraction (where the numerator is larger than the denominator) is perfectly acceptable. However, you can convert it to a mixed number (a whole number and a fraction) for easier interpretation. For example, 8/3 can be expressed as 2 2/3.
Q4: How can I practice dividing fractions?
A4: Practice is key! Start with simple examples and gradually increase the complexity. Online resources and textbooks provide numerous practice problems with varying difficulty levels. You can also create your own word problems to solidify your understanding.
Q5: What happens if I divide by zero?
A5: Division by zero is undefined in mathematics. It's a fundamental concept that doesn't have a numerical solution. Therefore, you should never attempt to divide any number by zero.
Advanced Concepts: Applications in Real-World Scenarios
Understanding fraction division is not just an abstract mathematical concept; it has widespread applications in various real-world scenarios.
- Baking and Cooking: Recipe adjustments often require dividing fractional amounts of ingredients.
- Construction and Engineering: Precise measurements and calculations involving fractions are essential in many construction projects.
- Finance: Dividing shares or calculating proportions in investments involves fractional calculations.
- Science and Research: Data analysis and scientific experiments frequently utilize fractions and their operations.
Conclusion: Mastering Fraction Division
Mastering fraction division opens doors to a deeper understanding of mathematics and its applications in real-world contexts. By understanding the concept of reciprocals and applying the simple rule of inverting and multiplying, you can confidently tackle a wide range of problems. Remember that consistent practice and a firm grasp of the underlying principles are crucial to building a strong foundation in mathematics. Don't be discouraged if you find it challenging at first; persistence and a focused approach will lead you to success. The key is to break down the problem into smaller, manageable steps and understand the "why" behind each step, not just the "how."
Latest Posts
Latest Posts
-
How Many Inches Are In 1 Km
Sep 08, 2025
-
O Is The Midpoint Of Segment Fg
Sep 08, 2025
-
Can A Right Triangle Be An Obtuse Triangle
Sep 08, 2025
-
A Ball Is Shot From The Ground Into The Air
Sep 08, 2025
-
Domain And Range Of Ordered Pairs
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 1/5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.