3 4x 2 20x 9x 2
faraar
Sep 08, 2025 · 5 min read
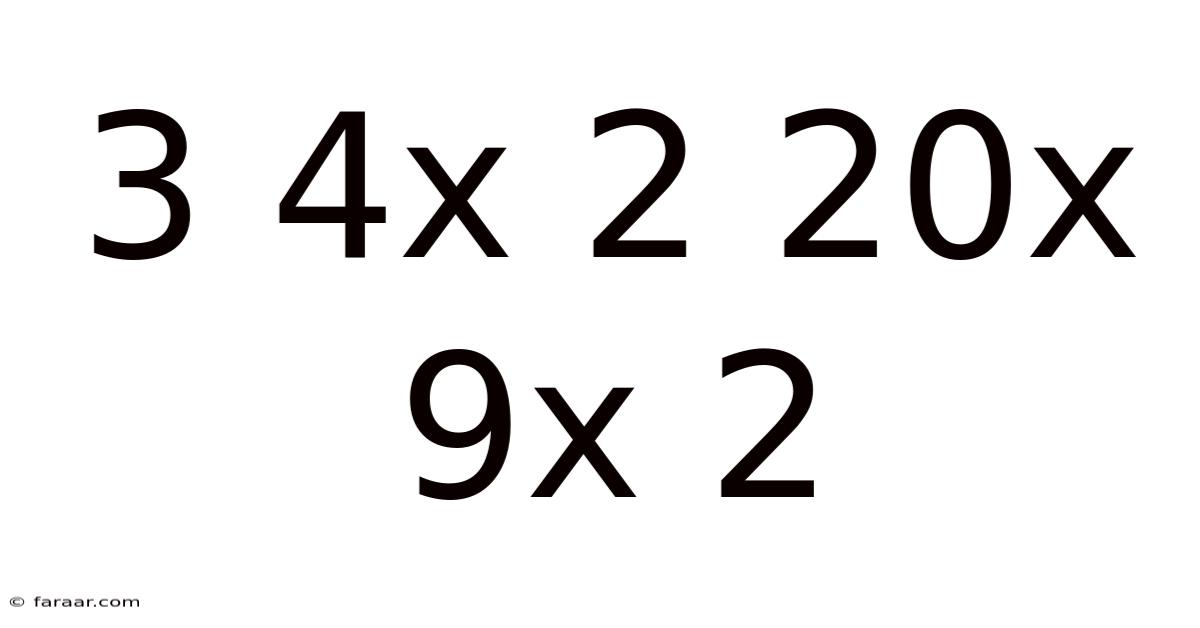
Table of Contents
Decoding the Mathematical Puzzle: 3 4x 2 20x 9x 2
This article delves into the intriguing mathematical puzzle presented by the sequence "3 4x 2 20x 9x 2". At first glance, it appears cryptic, a jumble of numbers and symbols. However, upon closer examination, we can uncover the underlying logic and principles at play. This seemingly simple sequence offers an excellent opportunity to explore various mathematical concepts, including order of operations, pattern recognition, and potentially, even more advanced algebraic structures depending on the intended interpretation. We'll unpack this puzzle step-by-step, considering different possible solutions and exploring the underlying mathematical reasoning. Understanding this sequence helps hone critical thinking and problem-solving skills.
Understanding the Problem
The core challenge lies in deciphering the meaning of the "x" symbol within the sequence. Does it represent traditional multiplication? Or does it signify a different mathematical operation entirely? This ambiguity is the key to the puzzle's complexity. To solve it, we need to explore different interpretations and test their validity.
Possible Interpretations and Solutions
Interpretation 1: Standard Multiplication
If we assume "x" represents standard multiplication, the sequence becomes: 3 * 4 * 2 * 20 * 9 * 2. This is a straightforward calculation:
- 3 * 4 = 12
- 12 * 2 = 24
- 24 * 20 = 480
- 480 * 9 = 4320
- 4320 * 2 = 8640
Therefore, under this interpretation, the solution is 8640. This is a valid solution, but it doesn't necessarily explore the potential for deeper mathematical meaning within the sequence.
Interpretation 2: Hidden Operations or Patterns
Let's consider the possibility that the sequence hides more complex operations or patterns. We might need to look for:
-
Alternating Operations: Perhaps "x" alternates between multiplication and another operation, such as addition, subtraction, or division. This would require a careful examination of the numerical relationships between consecutive terms.
-
Recursive Relationships: The sequence could be defined recursively, where each term depends on the previous one or several preceding ones.
-
Modular Arithmetic: Could the sequence operate within a specific modulo (remainder after division)? This would introduce a cyclical nature to the sequence.
-
Base Conversion: The numbers could be representations in different bases (e.g., binary, ternary, etc.), requiring conversion to a common base for calculation.
Let's explore some possibilities based on these hypotheses.
Example of an Alternate Interpretation (Hypothetical):
Let's assume a pattern where we alternate between multiplication and addition. The sequence would be interpreted as:
(3 * 4) + 2 - (20 * 9) + 2 = 12 + 2 - 180 + 2 = -164
This interpretation yields a different result (-164). The point is that without further information or context, there are many valid ways to interpret the sequence.
Expanding on Mathematical Concepts
This puzzle provides a fantastic opportunity to discuss several core mathematical concepts:
-
Order of Operations (PEMDAS/BODMAS): The order in which operations are performed significantly impacts the outcome. In standard arithmetic, multiplication and division take precedence over addition and subtraction. This principle is crucial when evaluating mathematical expressions.
-
Pattern Recognition: Identifying patterns is a fundamental skill in mathematics and problem-solving. Looking for sequences, repetitions, or relationships between numbers allows us to generalize and make predictions. Recognizing patterns often helps in unraveling seemingly complex problems.
-
Algebraic Thinking: Algebra involves using symbols and variables to represent unknown quantities and relationships. When we analyze the sequence "3 4x 2 20x 9x 2", we essentially engage in algebraic thinking – trying to identify the meaning of "x" and the underlying rules governing the sequence.
-
Number Systems and Bases: While not explicitly involved in the simplest interpretation, the possibility of working in different number bases highlights the flexibility and abstraction in mathematics. Understanding number bases is crucial in computer science and other fields.
-
Functional Relationships: We can think of this sequence as a function. If 'x' represents a specific operation, the function takes the sequence of numbers as input and produces a single output. This is a powerful way to view the puzzle from a higher-level mathematical perspective.
The Importance of Context
The key to definitively solving this puzzle lies in the context in which it was presented. Was this a casual puzzle, a problem from a math textbook, or part of a larger coded message? The source significantly impacts our approach.
For instance:
-
A casual puzzle: In a casual setting, the simplest interpretation (standard multiplication resulting in 8640) would likely suffice.
-
A textbook problem: A math textbook would likely provide additional clues or instructions. It might specify the operation represented by "x" or introduce a more complex system.
-
A coded message: If this sequence is part of a coded message, the "x" symbol could represent a more elaborate substitution or encryption technique. Breaking the code might require deciphering a key or pattern related to the numbers themselves or their positions.
Frequently Asked Questions (FAQ)
Q: Is there only one correct answer?
A: Without further information or context, there isn't a single definitive answer. The interpretation of "x" is crucial, and multiple valid interpretations lead to different results.
Q: What are some strategies for solving similar puzzles?
A: Look for patterns, test different interpretations, consider the order of operations, and explore different mathematical concepts. If the puzzle is from a specific source, consider its context.
Q: How can this puzzle be adapted for different skill levels?
A: For younger learners, focus on the basic multiplication interpretation. For advanced learners, introduce the concept of alternative operations or explore more complex mathematical ideas, such as modular arithmetic or base conversions.
Q: Why is this type of puzzle valuable in education?
A: Puzzles like this promote critical thinking, problem-solving, and mathematical reasoning. They encourage learners to explore, experiment, and justify their solutions, fostering a deeper understanding of mathematical concepts.
Conclusion
The mathematical puzzle "3 4x 2 20x 9x 2" is a deceptively simple yet multifaceted problem. Its ambiguity allows for various interpretations and solutions, providing a rich environment for exploring different mathematical concepts. The key takeaway is not just finding a single "correct" answer but rather understanding the process of interpreting ambiguous information, applying mathematical principles, and testing different hypotheses. This puzzle serves as a microcosm of the larger mathematical landscape: a seemingly straightforward problem can open up a wide range of possibilities and avenues for intellectual exploration. This underscores the importance of critical thinking, flexible problem-solving, and a thorough understanding of fundamental mathematical operations and principles. The seemingly simple sequence teaches us that context is king and a multitude of solutions might be equally valid, depending on the frame of reference.
Latest Posts
Latest Posts
-
A Rectangular Fence Surrounds A Vegetable Garden
Sep 08, 2025
-
How Many Gallons Is A Quarter Tank Of Gas
Sep 08, 2025
-
Evaluate 3 To The Power Of 3
Sep 08, 2025
-
How Is Alaska The Most Eastern State
Sep 08, 2025
-
How To Find The Perimeter Of A Polygon With Vertices
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 3 4x 2 20x 9x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.