3/4 Divided By 12 As A Fraction
faraar
Sep 11, 2025 · 6 min read
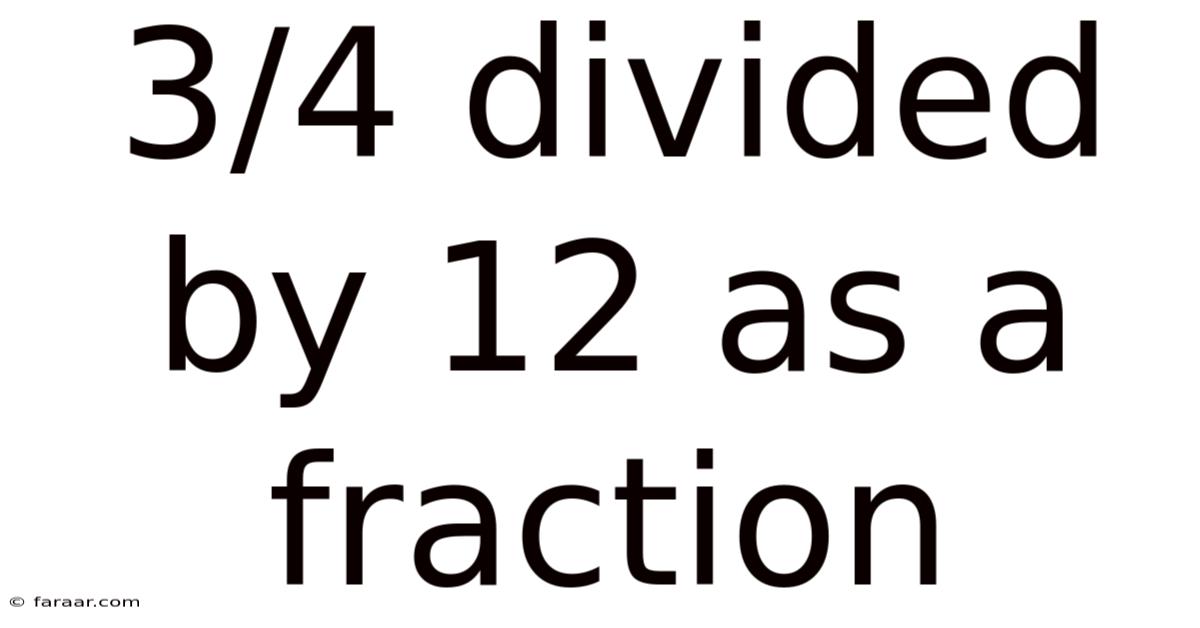
Table of Contents
Understanding 3/4 Divided by 12: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will guide you through the steps of solving 3/4 divided by 12, explaining the underlying principles and offering different approaches to reach the solution. We'll explore the concept of reciprocals, the visual representation of division, and address frequently asked questions. By the end, you'll not only know the answer but also possess a solid grasp of fractional division. This comprehensive guide will delve into the intricacies of dividing fractions, making this seemingly complex math problem easily understandable.
Introduction: Deconstructing the Problem
The problem before us is to solve 3/4 ÷ 12. This involves dividing a fraction (3/4) by a whole number (12). Many find this type of problem challenging, but breaking it down into manageable steps makes the solution clear. We'll tackle this problem using multiple methods, showcasing the flexibility and understanding required for successful fraction manipulation. This understanding will not only help you solve this specific problem but will equip you with the skills to tackle similar problems with confidence.
Method 1: Converting the Whole Number to a Fraction
The first approach involves converting the whole number 12 into a fraction. Any whole number can be represented as a fraction with a denominator of 1. Therefore, 12 can be written as 12/1. This transformation allows us to apply the standard rule for dividing fractions.
The rule for dividing fractions states: To divide one fraction by another, you multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply the fraction flipped upside down.
Following this rule:
-
Step 1: Rewrite the problem: 3/4 ÷ 12/1
-
Step 2: Find the reciprocal of the second fraction: The reciprocal of 12/1 is 1/12.
-
Step 3: Change division to multiplication: 3/4 x 1/12
-
Step 4: Multiply the numerators and the denominators: (3 x 1) / (4 x 12) = 3/48
-
Step 5: Simplify the fraction: Both 3 and 48 are divisible by 3. 3 ÷ 3 = 1 and 48 ÷ 3 = 16. Therefore, the simplified answer is 1/16.
Method 2: Visualizing the Division
Imagine you have a pizza cut into four equal slices. You possess three of those slices (3/4 of the pizza). Now, you need to divide those three slices among 12 people. How much pizza does each person get?
To visualize this, consider dividing each of your three slices into 12 equal parts. This results in a total of 3 x 12 = 36 smaller pieces. Since you have 3 slices, you have 36 smaller pieces to share among 12 people. Each person receives 36 ÷ 12 = 3 smaller pieces.
Since the original pizza was divided into 4 slices, and we further divided each slice into 12 parts, the pizza is now divided into 4 x 12 = 48 total pieces. Each person receives 3 out of 48 pieces, giving us the fraction 3/48. This simplifies to 1/16, the same result as the first method. This visual approach provides an intuitive understanding of the division process.
Method 3: Using Decimal Representation
Although not strictly a fractional method, converting the fraction and whole number into decimals can provide an alternative path to the solution.
-
Step 1: Convert the fraction to a decimal: 3/4 = 0.75
-
Step 2: Divide the decimal by the whole number: 0.75 ÷ 12 = 0.0625
-
Step 3: Convert the decimal back to a fraction: To convert 0.0625 to a fraction, we can express it as 625/10000. Simplifying this fraction by dividing both the numerator and denominator by their greatest common divisor (625), we get 1/16.
While this method works, it's generally less efficient and can lead to rounding errors if dealing with more complex fractions. The fractional methods are generally preferred for accuracy and conceptual clarity.
The Importance of Simplification
In all the methods above, we arrived at the fraction 3/48 before simplification. Simplifying fractions is crucial for two main reasons:
-
Clarity: A simplified fraction is easier to understand and interpret. 1/16 is much clearer than 3/48.
-
Standardization: In mathematics, it's standard practice to express fractions in their simplest form. This ensures consistency and avoids ambiguity.
Simplifying involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by that GCD. In the case of 3/48, the GCD is 3.
Explanation of the Underlying Mathematical Principles
The core principle at play here is the relationship between division and multiplication. Division is the inverse operation of multiplication. When we divide 3/4 by 12, we are essentially asking: "What number, when multiplied by 12, equals 3/4?"
The use of reciprocals in the first method is directly related to this inverse relationship. Multiplying by the reciprocal is mathematically equivalent to dividing by the original fraction. This method provides a structured approach to solving fractional division problems.
Frequently Asked Questions (FAQs)
Q: Can I divide the numerator and denominator of 3/4 by 12 directly?
A: No. Dividing only the numerator or denominator by 12 would alter the value of the fraction. You must use the methods described above to maintain the correct proportionality.
Q: What if the whole number was a fraction as well?
A: The process remains the same. You would simply multiply the first fraction by the reciprocal of the second fraction, as outlined in Method 1.
Q: Why is simplification important?
A: Simplification makes the fraction easier to understand and compare with other fractions. It also presents the answer in a standardized form.
Q: Are there other ways to solve this problem?
A: While the methods discussed are the most common and efficient, other approaches might exist depending on the context or specific mathematical tools being utilized. However, these methods provide a robust and widely applicable solution.
Conclusion: Mastering Fractional Division
Dividing 3/4 by 12 results in 1/16. This article has explored multiple methods to reach this answer, emphasizing the importance of understanding the underlying principles. Whether you prefer the algebraic approach using reciprocals, the visual representation of the problem, or the decimal conversion method, the key is to grasp the fundamental concept of fractional division. Mastering this skill will significantly enhance your understanding of fractions and pave the way for tackling more complex mathematical problems. Remember to always simplify your answer to its lowest terms for clarity and consistency. Through practice and a firm grasp of these methods, fractional division will become second nature.
Latest Posts
Latest Posts
-
Another Way Of Saying You Re Welcome
Sep 11, 2025
-
Evaluate Each Limit Given That
Sep 11, 2025
-
Which Of The Following Statements About Bonding Is True
Sep 11, 2025
-
Greatest Common Factor Of 20 And 40
Sep 11, 2025
-
How Many Feet Of Ribbon To Make A Bow
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Divided By 12 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.